Calcul littéral : exercices de maths en 3ème corrigés en PDF.
Mis à jour le 13 décembre 2025
Exercice 1 – Développer avec les identités remarquables.
Développer en utilisant les identités remarquables :
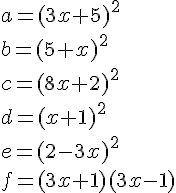
Exercice 2 – Développer une expression littérale.
On donne A = (3x-5) (6-4x)-5(8-6x)
1. Développer et réduire A .
2. Calculer la valeur exacte de A si 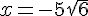 ; donner ensuite la valeur arrondie au centième .
; donner ensuite la valeur arrondie au centième .
Exercice 3 – Développer les expressions littérales.
Développer et réduire les expressions suivantes :
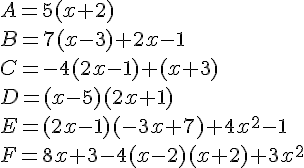
Exercice 4 – Développer puis réduire.
Développer, puis réduire, si possible, chaque expression :
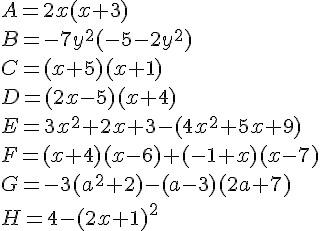
Exercice 5 – Calcul numérique.
Calculer sans calculatrice et sans poser d’opérations :
1. 101²
2. 103²
3. 98²
4. 101×99
Exercice 6 – Développer les expressions littérales.
Développer les expressions littérales suivantes et les réduire.
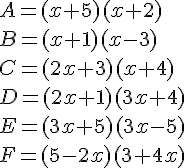
Exercice 7 – Développement à l’aide d’identités remarquables.
Développer ces expressions littérales et détailler toutes les étapes:
a) (x-1)²
b) (x+4)²
c) (2x+1)²
d) (7x-1)(7x+1)
e) (4x-1)(3x+7)
f) (-x+1)(3x-2)
g) (1/2+x)²
h) (x-4)²+(x+2)(x+3)
i) (5x-3)(2x+1)-(x+1)²
Exercice 8 – Développer, réduire et identités remarquables.
Développer et réduire les expressions suivantes :
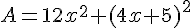
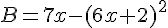
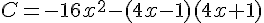
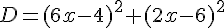
Exercice 9 – Identités remarquables.
Développer à l’aide des identités remarquables
et réduire les expressions :
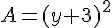
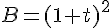
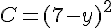
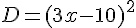
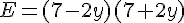
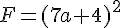
Exercice 10 – Factoriser les expressions littérales.
Factoriser ces expression algébriques.
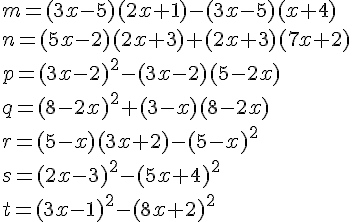
Exercice 11 – Factoriser les expressions.
Factoriser ces expression littérales.
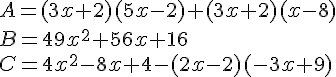
Exercice 12 – Calcul littéral et brevet des collèges.
On considère l’expression :
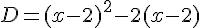
1. Factoriser D.
2. Développer et réduire D.
3. Calculer D pour x = 1 .
Exercice 13 – Développer, réduire et factoriser.
On considère l’expression :
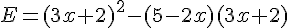
1. Développer et réduire l’expression E.
2. Factoriser E.
3. Calculer E pour x = – 2.
Exercice 14 – Développer et réduire.
Soit l’expression suivante :
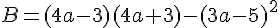
1. Développer et réduire l’expression B.
2. Calculer l’expression B pour :
a. a=1; b. a=0,75; c. a=0 .
Exercice 15 – Factoriser et identité remarquable.
Factoriser les expressions littérales suivantes :
K = (x + 1)² + (x + 1)(3x + 1)
L = (x – 3)² – (x – 3)(4x + 1)
M = (x + 1)(2x – 5) + (2x – 5)²
Exercice 16 – Factoriser les expressions littérales.
E = (x – 3)(2x + 1) + 7(2x + 1)
F = (x + 1)(x + 2) – 5(x + 2)
G = (3 – x)(4x + 1) – 8(4x + 1)
Exercice 17 – Factoriser les expressions.
A = 13(x + 2) + 5(x + 2)
B = 3x(x + 2) – 5(x + 2)
C = 4(x + 3) + 9x(x + 3)
D = 7x(3x + 1) – 10x(3x + 1)
Exercice 18 – Factorisations un peu plus complexes.
Factoriser les expressions suivantes :
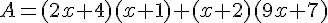
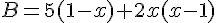
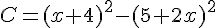
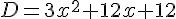

Exercice 19 – Factorisation d’expressions littérales.
Développer les expressions suivantes :

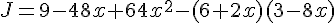
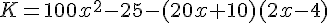
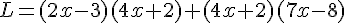
puis factoriser-les.
Exercice 20.
1. Factoriser :
a. 9-12x+4x² .
b. (3-2x)²-4 .
2. En déduire une factorisation de : E = (9-12x+4x²)-4 .
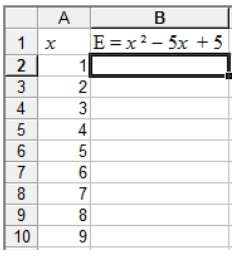
Exercice 21 – Utilisation du tableur.
On considère les expressions E = x² − 5x + 5 et F = (2x − 7)(x − 2) − (x − 3)² .
a) Calculer E et F pour x = 4.
b) Développer F. Les résultats obtenus à la question a) sont−ils surprenants ?
c) Avec un tableur :
On veut calculer en colonne B les valeurs prises par l’expression E pour les valeurs de x inscrites en colonne A.
Quelle formule faut-il rentrer dans la cellule B2 pour faire effectuer le calcul souhaité ?
(la formule devra pouvoir être étendue aux cellules situées en dessous)
Exercice 22 – Développer, factoriser et résoudre.
On considère l’expression 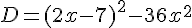 .
.
1) Développer et réduire D.
2) Factoriser D.
3) Résoudre l’équation 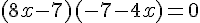 .
.
4) Calculer la valeur exacte de D quand 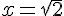 .
.
Exercice 23 – Factoriser et développer.
1. Factoriser ces expressions :
A=36-25x²
B=100+60x+9x²
C=b²-10b²+25
E=(2-x)²+(2-x)(9-x)
2. Développer les expressions littérales suivantes :
A=(2x-5)²
B=(5x-3)(5x+3)
C=(-3x+5)²
D=(-6x+9)²
Exercice 24 – Calcul littéral : développer et factoriser.
A = (2x – 3)(2x + 3) – (3x + 1)(2x – 3)
1. Développer puis réduire A.
2. Factoriser A.
3. Résoudre l’équation : (2x – 3)(-x + 2) = 0
Exercice 25 – Problème classique.
On donne : D = (2x – 3)(5x + 4) + (2x – 3)².
1.Montrer, en détaillant les calculs, que D peut s’écrire :
D = (2x – 3)(7x + 1)
2. Résoudre l’équation : (2x – 3)(7x + 1) = 0.
Exercice 26 – Développer, réduire et factoriser.
Soit E=(3x+2)²-(3x+2)(x+7) .
a) Développer et réduire E .
b) Factoriser E .
c) Calculer E pour 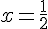 .
.
Exercice 27 – Compléter les identités remarquables.
Compléter en utilisant les identités remarquables .
A= (3x+…)²=…+…+25
B= (2x-…)²=…-24x+…
C=(… … …)² = …-16y+16
D= 49a²+…+25 = (… … …)²
E = 4x²-…= (…-…)(…+1)
Exercice 28 – Identités remarquables.
Développer à l’aide des identités remarquables puis réduire.
A = (x + 5) ²
B = (3x – 7) ²
C = (x + 4) (x – 4)
D = (9b + 7) ²
E = (7x + 1) (7x – 1)
Exercice 29.
Factoriser à l’aide des identités remarquables.
A = x² + 6x + 9
B = 9x² – 12x + 4
C = y² – 9
D = 16a² – 81
E = 49a² +70a +25
F = 144 – 121a²
G = (2x + 5)² – 9
H = (2x + 1)² – (3x + 5)²
Exercice 30.
Utiliser l’identité remarquable pour calculer mentalement les expressions suivantes.
A = 102² B = 99×101 C = 99²
Exercice 31.
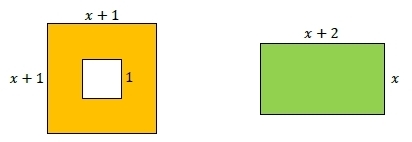
Sur ces figures, les longueurs sont exprimées en mètre.
1. Exprimer l’aire A en fonction de x .
Factoriser l’expression obtenue.
2. Exprimer l’aire B en fonction de x .
3. Pour quelle(s) valeur(s) de x ces deux aires sont-elles égales ?
Exercice 32.
On donne E = (2x+3)² – 16.
1. Montrer que E peut s’écrire 4x² + 12x – 7.
2. Calculer E pour : x = 2 ; x = 1.
3. Factoriser E.
Développer l’expression obtenue.
Quel est le résultat?
Exercice 33.
1. Calculer A et B en donnant le résultat sous forme de fractions irréductibles .
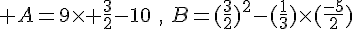 .
.
2. On considère l’expression : 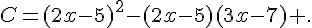
a. Développer et réduire C .
b. Factoriser l’expression C .
c. résoudre l’équation : (2x-5)(2-x)=0 .
Exercice 34.
1.a. Développer et réduire l’expression : D = (2x+5)(3x-1) .
b. Développer et réduire l’expression : E=(x-1)²+x²+(x+1)² .
Application : déterminer trois nombres entiers positifs consécutifs, (x-1), x et (x+1) dont la somme des carrés est 4 802 .
2.a. Factoriser l’expression : F=(x+3)²-(2x+1)(x+3) .
b. Factoriser l’expression : G=4x²-100 .
Application : déterminer un nombre positif dont le carré du double est égal à 100 .
Exercice 35.
On pose E=(4x-3)²+6x(4-x)-(x²+9).
a. Montrer que E est égal au carré de 3x .
b. Trouver les valeurs de x pour lesquelles E=144 .
c. Calculer la valeur de E pour 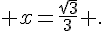
Exercice 36 – Programme de calcul .
On donne un programme de calcul :
- Choisir un nombre.
- Lui ajouter 4.
- Multiplier la somme obtenue par le nombre choisi.
- Ajouter 4 à ce produit.
- Ecrire le résultat .
1. Ecrire les calculs permettant de vérifier que si l’on fait fonctionner ce programme
avec le nombre – 2 alors on obtient 0.
2. Donner le résultat fourni par le programme lorsque le nombre choisi est 5.
3. On note x le nombre choisi
Quelle est l’expression littérale obtenue en effectuant ce programme.
Donner le résultat sous forme développé.
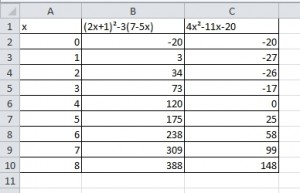
Exercice 37 – Utilisation du tableur pour le calcul littéral.
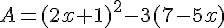
Baptiste développe et réduit A.
Il obtient 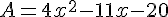 .
.
Il réalise alors la feuille de calcul ci-dessous pour contrôler son résultat.
1.Quelle formule a-t-il écrite en cellule B2 et étendue à la cellule B10 ?
2.Quelle formule a-t-il écrite en cellule C2 et étendue à la cellule C10 ?
3.Observer cette feuille de calcul. Que penser alors de la réponse de Baptiste ?Expliquer.
4.Développer et réduire l’expression initiale de A.
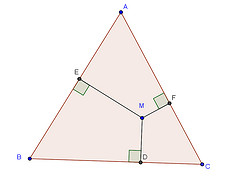
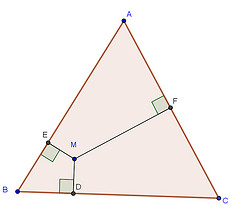
Exercice 38 – Problème ouvert de géométrie et compétences.
Le problème est le suivant. On a un triangle équilatéral ABC, un point M, d’humeur bucolique qui se promène dans le triangle.
On appelle D, E et F les pieds des perpendiculaires en M au trois côtés du triangle.
Question : Où doit-on placer M pour que la somme MD+ME+MF soit minimale ?
Exercice 39 – Problème ouvert sur l’aire d’un carré.
Construire un carré ayant pour aire le double du carré ci-dessus.
Détaillez votre méthode.
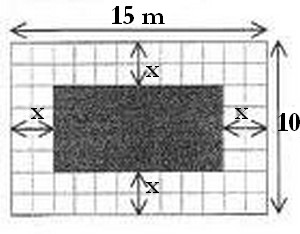
Exercice 40 – Problème d’une piscine.
Jacques a fait construire une piscine rectangulaire .
Il a carrelé le bord de cette piscine .
Les longueurs sont exprimées en mètre .
1) Exprimer en fonction de  l’aire
l’aire 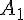 de la surface de la piscine .
de la surface de la piscine .
2) Exprimer en fonction de  l’aire
l’aire 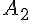 de la surface carrelée .
de la surface carrelée .
3) Développer et réduire l’expression obtenue pour 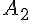 .
.
4) Calculer les aires 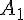 et
et 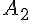 pour
pour 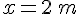 .
.
Exercice 41 – Trois entiers consécutifs.
a) Choisir 3 nombres entiers consécutifs (qui se suivent).
Calculer le carré du nombre du milieu, puis soustraire à ce carré le produit des deux autres nombres.
b) Recommencer avec 3 autres nombres entiers consécutifs. Que constate-t-on ?
c) Démontrer cette conjecture.
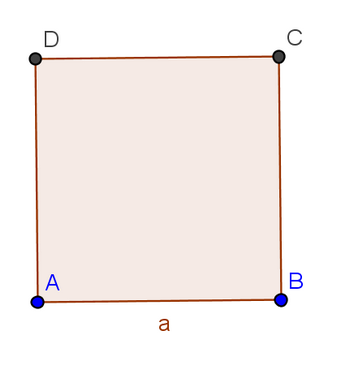
Exercice 42 – Géométrie et calcul littéral.
1) Résoudre l’inéquation : 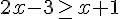 et représenter les solutions sur une droite graduée.
et représenter les solutions sur une droite graduée.
2) x désignant un nombre supérieur ou égal à 4,
ABCD est un carré dont le côté mesure 2x – 3.
a. Montrer que l’aire du rectangle BCEF s’exprime par la formule :

b. Développer et réduire A.
c. Factoriser A.
d. Résoudre l’équation : (2x – 3)(x – 4) = 0
e. Pour quelles valeurs de x, l’aire du rectangle BCEF est-elle nulle ? Justifier .
Exercice 43 – Programme de calcul.
On donne le programme de calcul suivant :
- Choisir un nombre.
- Ajouter 1.
- Calculer le carré du résultat obtenu.
- Soustraire le carré du nombre de départ.
- Soustraire 1.
1. a. Effectuer ce programme lorsque le nombre choisi est 10 et montrer qu’on obtient 20.
b. Effectuer ce programme lorsque le nombre choisi est −3 et montrer qu’on obtient −6.
c. Effectuer ce programme lorsque le nombre choisi est 1,5.
2. Quelle conjecture peut-on faire à propos du résultat fourni par ce programme de calcul ?
Démontrer cette conjecture.
Exercice 44 – Expression littérale qui ne s’annule pas.
Riyane affirme :
« Pour tout nombre entier N l’expression de  est toujours différente de zéro ».
est toujours différente de zéro ».
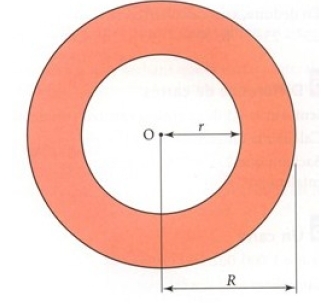
Exercice 45 – Aire d’une couronne.
Démontrer que l’aire de la couronne de centre O représentée ci-dessous est égale à
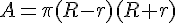
Exercice 46 – Aire et identités remarquables.
1. Calculer les aires colorées des deux figures ci-dessous en fonction de x .
2. Que remarque-t-on ?
Exercice 47 :
Développer puis réduire chaque expression.
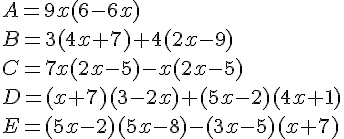
Exercice 48 :
Développer et réduire l’expression suivante :
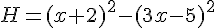
Exercice 49 :
Dans chaque cas, une seule réponse est exacte.
Recopier la bonne réponse.
a. Si l’on développe et réduit l’expression (x + 2)(3x-1),
on obtient :
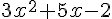 ou
ou 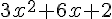 ou
ou 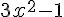
b. La forme développée de 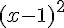 est:
est:
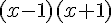 ou
ou  ou
ou 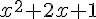 .
.
c. Une expression factorisée de 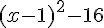 est:
est:
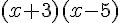 ou
ou 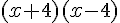 ou
ou 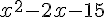 .
.
d. Une expression factorisée de 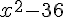 est :
est :
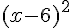 ou
ou  ou
ou 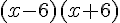 .
.
Exercice 50 :
a. Donner le résultat fourni par le programme de calcul si l’on choisit comme
nombre de départ :
-2 ; 5 puis 10.
b. Montrer que le résultat obtenu est toujours le carré d’un nombre entier.
Exercice 51 :
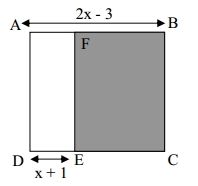
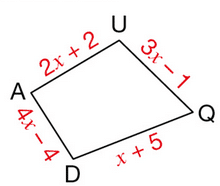
L’unité de longueur est le centimètre.
x désigne un nombre (x > 1).
a. Pour quelle valeur de x le périmètre du quadrilatère QUAD est-il 32 cm ?
b. Quelle est alors la nature quadrilatère QUAD ?
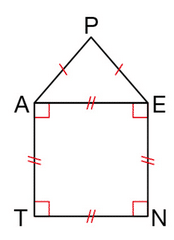
Exercice 52 :
AENT est un carré dont le périmètre est 56 cm.
PAE est un triangle isocèle en P.
a. Calculer AE.
b. Pour quelle longueur de [AP] le périmètre du pentagone PENTA est-il égal à 60 cm ? Justifier.
Exercice 53 :
Développer les expressions littérales suivantes :
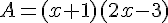
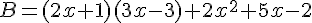
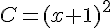
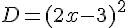
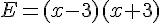
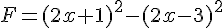
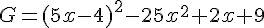
Exercice 54 :
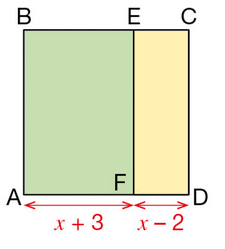
x désigne un nombre supérieur ou égal à 2.
ABCD est un carré et ABEF est un rectangle.
1. Exprimer en fonction de x;
a. la longueur AD ;
b. l’aire 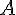 du carré ABCD ;
du carré ABCD ;
c. l’aire  du rectangle ABEF ;
du rectangle ABEF ;
d. l’aire ‘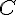 du rectangle ECDF.
du rectangle ECDF.
2. a. Exprimer les aires  et
et 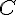 et leur somme sous forme développée et réduite.
et leur somme sous forme développée et réduite.
b. Vérifier que cette somme est égale à 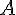 .
.
Exercice 55 :
Voici deux programmes de calcul.
a. Appliquer chaque programme aux nombres :
3 ; 10 et – 5 puis à un autre nombre choisi au hasard
Que constate-t-on ? Émettre une conjecture.
b. On note n le nombre choisi au départ.
Exprimer en fonction de n le résultat obtenu avec chaque programme.
Démontrer la conjecture émise à la question a.
Exercice 56 :
x désigne un nombre positif.
Voici un rectangle dont les côtés ont des longueurs variables.
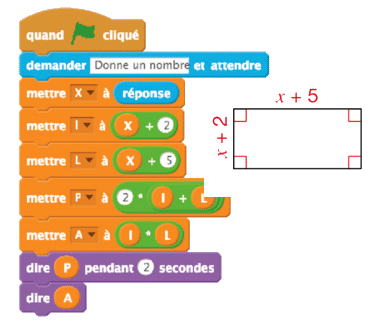
a. Léa a construit le programme ci-dessous avec le logiciel Scratch.
Que représentent les variables l et L ?
b. Quel est le rôle du programme de Léa ?
c. Léa affirme :«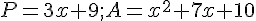 .»
.»
A-t-elle raison ? Expliquer.
d. Réaliser ce programme. Le tester en donnant à x la valeur 3, puis la valeur 10.
Exercice 57 :
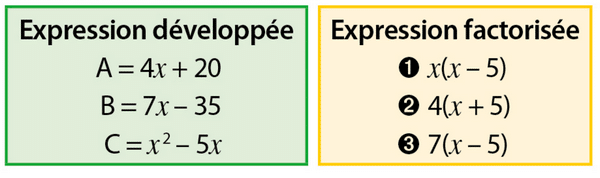
Associer chaque expression de gauche à sa forme factorisée de droite.
Exercice 58 :
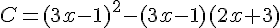 .
. .
.4) Calculer C pour 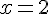 .
.
Exercice 59 :
Développer à l’aide du modèle indiqué.
Carré d’une somme | Carré d’une différence
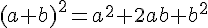 |
|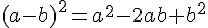
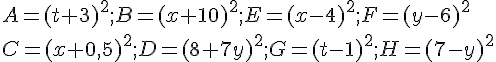
Exercice 60 :
On sait qu’en multipliant la somme de deux nombres par leur différence, on obtient :

Développer:
I=(x+8)(x-8) et J=(t-5)(t+5).
Exercice 61 :
Factoriser chaque expression avec une identité remarquable.
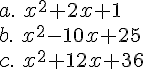
Exercice 62 :
Reconnaître une différence de deux carrés dans chaque expression, puis factoriser.
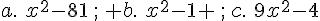
Exercice 63 :
Réduire chaque expression à l’aide d’une identité remarquable.
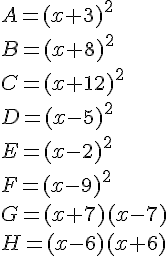
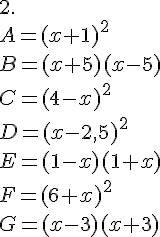
Exercice 64 :
Développer et réduire chaque expression.
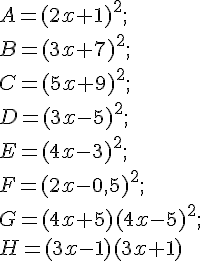
Exercice 65 :
x désigne un nombre relatif.
En utilisant des identités remarquables, recopier et compléter le tableau ci-dessous.
Exercice 66 :
Recopier et compléter à l’aide d’une identité remarquable.
a. 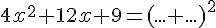
b. 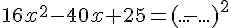
c. 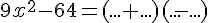
d.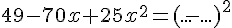
Exercice 67 :
Exercice 68 :
- Rappeler les trois identités remarquables.
- On veut développer
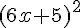 :
:
- Laquelle va-t-on utiliser ? Préciser alors la valeur de a et de b.
- Quel est le développement de
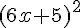 ?
?
Exercice 69 :
Compléter et terminer les développements :
a. 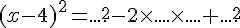 ;
;
b. 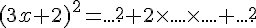
Exercice 70 :
Même exercice que le précédent.
a. 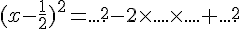
b. 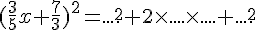
Exercice 71 :
Développer :
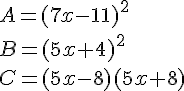
Exercice 72 :
Développer :
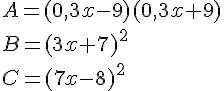
Exercice 73 :
Développer puis réduire :
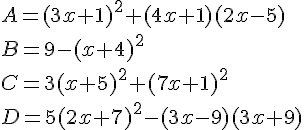
Exercice 74 :
Indiquer la forme factorisée de ces identités remarquables développées :
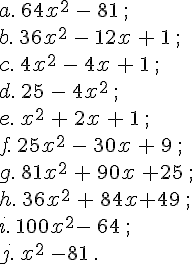
Exercice 75 :
Factoriser les expressions suivantes :
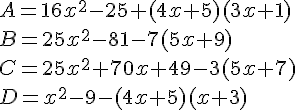
Exercice 76 :
1) Développer puis réduire 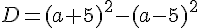 .
.
2) On pose 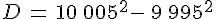 .
.
3) Sans utiliser la calculatrice et en se servant de la question 1, trouver la valeur de D.
Exercice 77 :
On donne  .
.
1) Développer et réduire E.
2) Factoriser E.
3) Développer l’expression obtenue à la question 2.
Quel est le résultat
Exercice 78 :
On donne 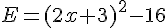 .
.
1) Montrer que E peut s ‘écrire 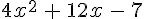 .
.
2) Calculer E pour : 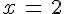 ;
; 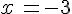 .
.
3) Factoriser E. Développer l’expression obtenue.
Quel est le résultat?
Exercice 79 :
- Réduire les expressions suivantes :
| A = 3x – 8 + 4x + 5 | B = 3x² + 5x – 6 – 2x² –4x – 3 | C = 5x² – 7 – 9x² +x – 3x + 9 |
| D = 4x² – (5x + x² – 6x) + 7x | E = 3x – (4 + 2x) + (x² + 7) | F = 3x² – (4x – 1) – (x² +5x) |
- Substituer à x sa valeur pour calculer chaque expression littérale :
| A = 7x – 3 Pour x = 5 |
B = x² + x – 9 Pour x = -2 |
C = -4x² – 2x + 2 Pour x = -3 |
| D = 2x – 7 + 3x + 1 Pour x = 4 |
E = (x – 3)² Pour x = -4 |
F = (2x – 3)(6 – x²) Pour x = 2 |
Exercice 80 :
- En utilisant l’identité « k(a + b) = ka + kb », développer les expressions suivantes :
| A = 7(x + 4) | B = 4(3 – 2x) | C = -3(x + 7) |
| D = -5(3x – 2) | E = -2x(5 + 4x) | F = 3x²(1 – 2x) |
- En utilisant l’identité « (a + b)(c + d) = ac + ad + bc + bd », développer les expressions suivantes :
| A = (x + 2)(x + 3) | B = (x – 7)(3x – 2) | C = (1 + 2x)(3 – x) |
| D = (-7x + 6)(5 – x²) | E = (3x + 4)(-x + 1) | F = (3x² – 4)(2x + 5) |
- Écrire le carré sous forme d’un produit puis développer les expressions suivantes :
| A = (x + 2)² | B = (1 + x)² | C = (2x + 1)² |
| D = (3 + 2x)² | E = (3x + 2)² | F = (x² + 5)² |
- Écrire le carré sous forme d’un produit puis développer les expressions suivantes :
| A = (x – 2)² | B = (x – 7)² | C = (2x + 5)² |
| D = (-4x + 3)² | E = (3x – 2)² | F = (x² – 3)² |
- En utilisant l’identité « (a + b)(c + d) = ac + ad + bc + bd », développer les expressions suivantes :
| A = (x + 2)(x – 3) | B = (x – 7)(x + 7) | C = (2x – 5)(2x + 5) |
| D = (3 – 4x)(3 + 4x) | E = (x² – 3x)(x² + 3x) | F = (2x² + 4)(2x² – 4) |
Exercice 81 :
En utilisant l’identité « ka + kb = k(a + b) », factoriser les expressions suivantes :
| A = 3x + 3y | B = 5x + 15 | C = 3 + 3a | |
| D = (2x + 1)(x + 4) + (2x + 1)(3x +2) | E = (x +7)² – (3x – 5)(x + 7) | ||
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «calcul littéral : exercices de maths en 3ème corrigés en PDF.» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.