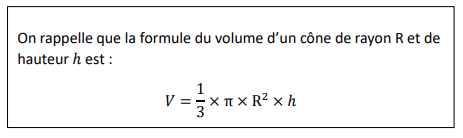Brevet de maths 2024 aux centres étrangers avec sujet et corrigé.

Le sujet et corrigé du brevet de maths 2024 aux centres étrangers. ce sujet permet aux élèves de réviser en ligne et se préparer pour le DNB du collège en mathématiques.

Ce sujet du brevet de maths 2024 aux centres étrangers porte sur un QCM sur le calcul numérique et les probabilités., les statistiques. L’étude d’un circuit d’entraînement avec la notion de vitesse moyenne et de proportionnalité. Un programme de calcul avec le calcul littéral et la double distributivité ainsi que, la résolution d’une équation du premier degré à une inconnue. L’étude d’une figure géométrique faisant intervenir le théorème de Thalès et de Pythagore puis, la trigonométrie et les homothéties. Puis, le calcul du volume d’un cône de révolution avec l’étude d’une section de solide.

Indications portant sur l’ensemble du sujet :
Toutes les réponses doivent être justifiées, sauf si une indication contraire est donnée.
Pour chaque question, si le travail n’est pas terminé, laisser tout de même une trace de la
recherche ; elle sera prise en compte dans la notation.

DIPLÔME NATIONAL DU BREVET
CENTRES ETRANGERS – SESSION 2024
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 100 points

L’utilisation de la calculatrice avec mode examen actif est autorisée.
L’utilisation de la calculatrice sans mémoire, « type collège » est autorisée.
Le sujet est constitué de cinq exercices indépendants.
Le candidat peut les traiter dans l’ordre qui lui convient.

Exercice 1 (20 points)
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n’est demandée.
Pour chaque question, quatre réponses sont proposées, une seule réponse est exacte.
Recopier sur la copie le numéro de la question et la réponse choisie.

1. Donner l’écriture scientifique de $0,193\,\times \,10^{-100}$ .

2. Lili part en vacances, elle parcourt 480 km en 5 h 42 min.
Quelle est sa vitesse moyenne en km/h, arrondie au dixième ?

3. Sam fait tourner la roue ci-dessous et regarde le nombre désigné par la flèche, qui peut être 1 ou 2.

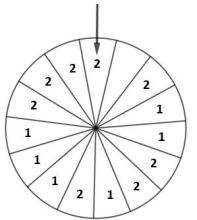
On admet que chaque secteur a autant de chance d’être désigné.
Le nombre écrit dans un des secteurs a été effacé.

Est-il possible d’écrire un nombre dans ce secteur de sorte que la probabilité
que la flèche désigne le nombre 2 soit égale à $\frac{3}{5}$ ?

4. On considère la liste de nombres suivante : 5 ; 1 ; 3 ; 10 ; 17 ; 11 ; 10. Pour cette liste de
nombres, que représente le nombre 5 ?

5. Léa achète un vélo électrique.

Pour le réserver, elle paye $\frac{1\,}{5}$ du prix au magasin.

Le magasin lui propose de payer le reste en trois paiements d’un même montant.

Quelle fraction du prix du vélo représente l’un de ces trois paiements ?

Exercice 2 (20 points)
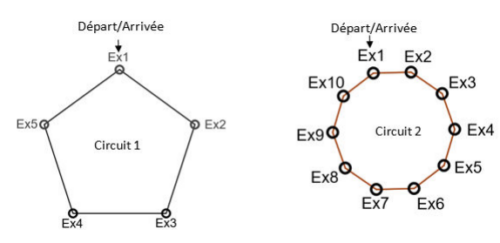
Un entraîneur de sport prépare deux circuits d’entraînement contenant plusieurs exercices de
cardio et de renforcement musculaire :
• un circuit commence à l’exercice 1 et se termine en revenant à l’exercice 1 ;
• le circuit 1 contient cinq exercices. Chaque exercice dure 40 secondes et doit être suivi de
16 secondes de repos permettant de se rendre à l’exercice suivant ;
• le circuit 2 contient dix exercices. Chaque exercice dure 30 secondes et doit être suivi de 5
secondes de repos permettant de se rendre à l’exercice suivant

1. Montrer que le circuit 1 s’effectue en 280 secondes et que le circuit 2 s’effectue en 350
secondes.
2. Donner la décomposition en produit de facteurs premiers de 280 et de 350.
3. Une séance d’entraînement est constituée de plusieurs tours du même circuit.
Au coup de sifflet de l’entraîneur, Camille commence une séance d’entraînement sur le circuit 1
et Dominique sur le circuit 2.
a. Expliquer pourquoi, lorsque 2 800 secondes se sont écoulées à partir du coup de sifflet,
Camille se trouve de nouveau au départ du circuit 1.
Préciser où se trouve Dominique sur le circuit 2 lorsque 2 800 secondes se sont écoulées.
b. Après le coup de sifflet, combien de temps faut-il à Camille et Dominique pour se retrouver
en même temps pour la première fois au départ de leur circuit ? Exprimer cette durée en
minute et seconde.

Exercice 3 (20 points)
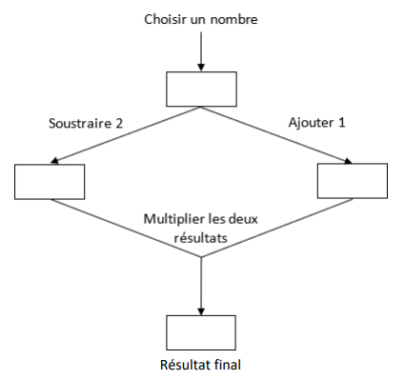
On considère le programme de calcul suivant :

Partie A
1. Justifier qu’en choisissant 5 comme nombre de départ, le résultat final obtenu est 18.
2. Calculer le résultat final donné par ce programme lorsque le nombre de départ choisi est $-\frac{3}{2}.$
3. Le script suivant, écrit avec un logiciel de programmation, correspond au programme de calcul ci-dessus.
Compléter les lignes 3, 4 et 5 du script. Aucune justification n’est attendue.

Partie B
Soit la fonction définie, pour un nombre donné, par $g(x)\,=\,x^2\,-\,x-\,2$ .
1. Prouver que $(x\,-\,2)(x\,+\,1)\,=\,x^2\,-\,x\,-\,2$ .
2. a. Résoudre l’équation $(x\,-\,2)(x\,+\,1)\,=\,0$ .
b. En déduire les antécédents de 0 par la fonction . Aucune justification n’est attendue.

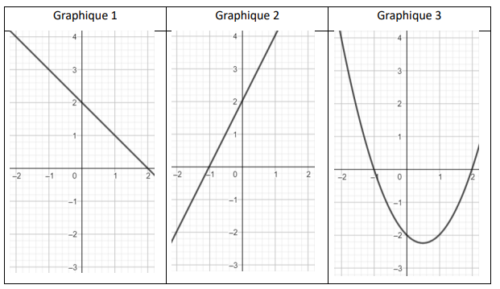
3. Parmi les trois graphiques ci-dessous, lequel correspond à la représentation graphique de la
fonction ? Aucune justification n’est attendue.

4. Quel(s) nombre(s) doit-on choisir comme nombre de départ pour que le programme de calcul
donne 0 comme résultat final ?

Exercice 4 (16 points)
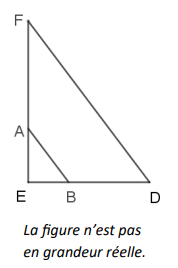
Sur la figure ci-dessous :
• les points E, A et F sont alignés ;
• les points E, B et D sont alignés ;
• les droites (FD) et (AB) sont parallèles ;
• AE = 4,4 cm ; EB = 3,3 cm ; AB = 5,5 cm et BD = 6,6 cm.

1. Démontrer que le triangle ABE est rectangle.
2. Calculer la mesure de l’angle $\widehat{ABE}$ , arrondie au degré.
3. Calculer la longueur FD.
4. Une homothétie de centre E transforme le triangle EAB en le triangle EFD.
Quel est le rapport de cette homothétie ? Aucune justification n’est attendue.

Exercice 5 (24 points)
Les deux parties sont indépendantes.
Partie A
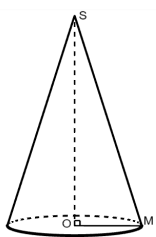
Léo veut fabriquer un chapeau en forme de cône pour se déguiser en sorcier lors de la fête d’Halloween.

Voici la représentation de ce chapeau en perspective cavalière.

Le rayon OM de la base de ce cône mesure 9 cm et la hauteur OS mesure 30 cm.

1. Démontrer que la longueur MS, arrondie au dixième de centimètre, est 31,3 cm.
2. Léo souhaite vérifier que le chapeau sera adapté à son tour de tête qui mesure 56 cm. Les
dimensions choisies pour concevoir le chapeau sont-elles adaptées au tour de tête de Léo ?
3. Léo a représenté ci-dessous le patron de son chapeau.
Il a reporté dessus les mesures des longueurs qu’il connaît et nommé l’arc de cercle de longueur
56,5 cm.

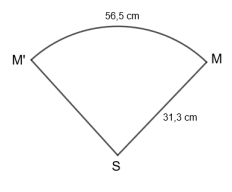
a. Démontrer que la longueur du cercle de centre S et de rayon SM, arrondie au dixième de
centimètre, est égale à 196,7 cm.

Pour dessiner en grandeur réelle son chapeau, il a besoin de calculer la mesure de l’angle
$\widehat{M'SM}$ qui est proportionnelle à la longueur de l’arc de cercle .

Il décide de représenter cette situation par le tableau de proportionnalité suivant :

b. Placer la valeur 196,7 obtenue à la question précédente dans le tableau.
c. Calculer la mesure de l’angle $\widehat{M'SM}$ correspondant à une longueur d’arc de 56,5 cm qui
permettra à Léo de tracer le patron de son chapeau. Donner le résultat arrondi au degré.

Partie B
On rappelle que la hauteur du chapeau mesure 30 cm.
1. Montrer que le volume total du chapeau, arrondi au , est de 2 545 .

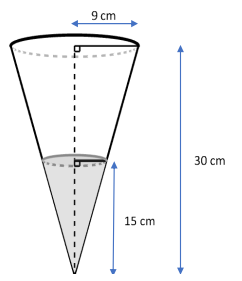
2. Léo décide d’utiliser son chapeau pour transporter les bonbons qu’il a récoltés pendant la fête
d’Halloween.

En arrivant chez lui, il constate que les bonbons atteignent le milieu de la hauteur
de son chapeau. Il estime que sa récolte de bonbons n’a pas été bonne car il pense que le
volume occupé par les bonbons représente moins de 15 % du volume total de son chapeau.
Son estimation est-elle correcte ?

Consulter le corrigé en ligne

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2024 aux centres étrangers avec sujet et corrigé.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.