statistiques : cours de maths en 3ème à télécharger en PDF gratuitement.

Sommaire de cette fiche

1 0- Vocabulaire général
2 I.Moyenne-étendue :
- 2.1 1. Définitions :
3 II. La médiane :
- 3.1 1.Définition:
4 Quartiles d’une série statistique :

Les statistiques dans un cours de maths en 3ème où nous aborderons la notion de population, de caractère qu’il soit quantitatif ou qualitatif puis, nous continuerons avec la notion de moyenne pondérée et de médiane ainsi que de l’utilisation du tableur. Dans cette leçon en troisième, nous représenterons des diagrammes en bâtons ou des histogrammes ainsi que des diagrammes circulaires appelés camembert.

0- Vocabulaire général

Définition et vocabulaire :

Lorsque l’on réalise une enquête, on est amené à étudier des caractères propres à chaque individu.

L’ensemble des individus est appelé la population.

Le caractère peut être qualitatif (la couleur des cheveux, les sports pratiqués ou le type de film préféré) ou quantitatif (la taille, l’âge, le temps passé devant la télévision, …).

Le nombre total d’individus de la population est appelé effectif total et noté N.

Le nombre d’individus qui possèdent un même caractère est appelé effectif du caractère.

La statistique est une branche des mathématiques qui étudie un caractère dans une population.

Exemples :

1) Étudier l’ensemble des notes d’un contrôle (caractère) dans une classe (population).

2) Etudier les intentions de vote pour des élections (caractère) sur un échantillon de 1 000 personnes.

Une série statistique est la donnée d’une série de nombres présentée sous la forme d’une liste ou d’un tableau.

Exemple : Relevé des notes d’un contrôle de maths.

I.Moyenne-étendue :

1. Définitions :

Définition 1 :

La moyenne d’une série statistique est le quotient de la somme de toutes les valeurs de cette série par l’effectif total.

Moyenne : $\overline{x}=\frac{n_1x_1+n_2x_2+....+n_px_p}{N}$

Avec : les effectifs.

: l’effectif total.

les valeurs du caractère .

Exemple 1:

On a une suite de notes: 5; 12; 19; 12; 8; 10; 11; 14; 3; 8; 7; 12; 10; 9; 8; 16; 14; 8; 5; 11.

Calculer la moyenne de ces notes:

$x=\frac{5+12+19+12+8+10+11+14+3+8+7+12+10+9+8+16+14+8+5+11}{20}=10,1$

Compléter le tableau suivant:

Notes	3	5	7	8	9	10	11	12	14	16	19
Nb d’élèves	1	2	1	4	1	2	2	3	2	1	1
Fréquence (%)	$\frac{1}{20}\times 100\simeq 5%$	10 %	5%	20%	5%	10%	10%	15%	10%	5%	5%

Calcul de la moyenne:

$\overline{x}=\frac{1\times 3+2\times 5+7\times 1+8\times 4+9\times 1+10\times 2+11\times 2+12\times 3+14\times 2+16\times 1+19\times 1}{20}=10,1$

Evidemment, nous retrouverons le même résultat avec la formule de la moyenne pour un caractère quantitatif .

2. Signification concrète de la moyenne :

Si tous les élèves avaient obtenu la même note, chacun aurait 10,1 sur 20.

Définition 2 :

L’étendue d’une série statistique est la différence entre la plus grande et la plus

petite valeur de la série.

Exemple : Dans la série précédente, l’étendue des notes est de: 19-3=16

II. La médiane :

1.Définition:

Définition :

On appelle médiane d’une série statistique ordonnée une valeur du caractère qui partage la

série en deux groupes de même effectif tels que :

· un groupe contient les valeurs inférieures ou égales à la médiane ;

· l’autre groupe contient les valeurs supérieures ou égales à la médiane.

Exemple 2: cas d’un nombre impair de valeurs.

Voici les notes d’un groupe de 9 élèves lors d’un devoir de mathématiques.

5-6-11-13-6-14-12-8-13

Il faut d’abord ranger les nombres dans l’ordre croissant : 5;6;6;8;11;12;13;13;14

Il y a 9 valeurs, 9 est un nombre impair .

La médiane sera la cinquième valeur.

La médiane de cette série statistique est : 11

Exemple 2: cas d’un nombre pair de valeurs.

Voici les notes d’un groupe de 6 élèves lors d’un devoir de sciences physiques.

6-13-18-16-14-5

Il faut d’abord ranger les nombres dans l’ordre croissant : 5;6;13;14;16;18.

Il y a 6 valeurs et 6 est un nombre pair.

La médiane est la moyenne de la troisième et quatrième valeur.

La médiane de cette série statistique est : $\frac{13+14}{2}=13,5$

2. Signification concrète de la médiane :

Il y a autant d’élèves qui ont eu au-dessous et au-dessus de 13,5 sur 20.

Quartiles d’une série statistique :

Définition :

Les valeurs de la série étant rangées dans l’ordre croissant.
– On appelle premier quartile la plus petite valeur, notée Q₁, de la série telle qu’au moins un quart (25 %) des valeurs soient inférieures ou égales à Q₁.

– On appelle troisième quartile la plus petite valeur, notée Q₃, telle qu’au moins trois quarts (75 %) des valeurs soient inférieures ou égales à Q₃.

Exemple :

Soit la série statistique suivante,qui représente des longueurs de pièces métalliques en milimètre.

Déterminons les quartiles.

19-53-31-3-79-8-34-3-9-11-44-19

Je range les valeurs par ordre croissant : 3;3;8;9;11;19;19;31;34;44;53;79

Il y a 12 valeurs.

$\frac{12}{4}=3$ donc le premier quartile est la troisième valeur soit 8 mm.

$\frac{3\times 12}{4}=9$ donc le troisième quartile est la neuvième valeur soit 34 mm.

Signification concrète :

Il y a moins de 25% des pièces qui mesurent en-dessous de 8 mm.

et il y a moins de 75 % des pièces qui mesurent en-dessous de 34 mm.

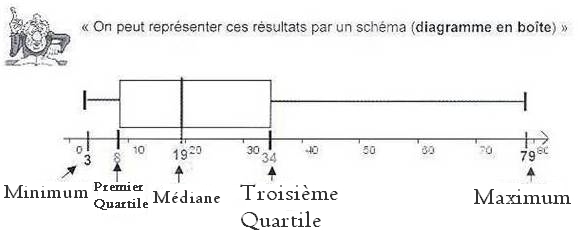
2.Diagramme en boîte :

4/5 - (67 votes)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «statistiques : cours de maths en 3ème» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés.

D'autres fiches similaires à statistiques : cours de maths en 3ème.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à statistiques : cours de maths en 3ème à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème statistiques : cours de maths en 3ème, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Les statistiques : cours de maths en 2de
62
Les statistiques dans un cours de maths en 2de où nous verrons la notion de population, de caractère quantitatif ou qualitatif. Nous aborderons la notion de fréquence et de moyenne pondérée d'une série statistiques ainsi que les différentes représentations graphiques dans cette leçon en seconde. I) Le vocabulaire des statistiques…
France 2017 : sujet du brevet de maths avec son corrigé
51
DIPLÔME NATIONAL DU BREVET SESSION 2017 PREMIÈRE ÉPREUVE 1ère partie MATHÉMATIQUES Série générale Durée de l’épreuve : 2 heures – 50 points THÉMATIQUE COMMUNE DE L’ÉPREUVE DE MATHÉMATIQUES-SCIENCES : L’ÉNERGIE Exercice 1 (4 points) Dans une urne contenant des boules vertes et des boules bleues, on tire au hasard une…

Les dernières fiches mises à jour

Voici les dernières ressources mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 2 365 085 cours et exercices de maths téléchargés en PDF et 181 073 membres.
Rejoignez-nous : inscription gratuite.