Brevet de maths 2018 en Amérique du Nord – sujet et corrigé
Mis à jour le 13 juillet 2025
Sujet du brevet de maths 2018 du collège en Amérique du nord le mardi 5 juin 2018.
Indication portant sur l’ensemble du sujet.
Toutes les réponses doivent être justifiées, sauf si une indication contraire est donnée.
Pour chaque question, si le travail n’est pas terminé, laisser tout de même une trace de la recherche;elle sera prise en compte dans la notation.
EXERCICE 1 : 14 POINTS
Le tableau ci-dessous a été réalisé à l’aire d’un tableur.
Il indique le nombre d’abonnements Internet à haut débit et à très haut débit entre 2014 et 2016, sur
réseau fixe, en France. (Sources : Arcep et Statistica).
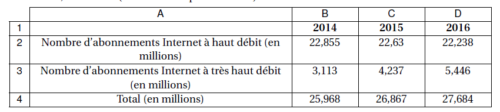
1. Combien d’abonnements Internet à très haut débit, en millions, ont été comptabilisés pour
l’année 2016?
2. Vérifier qu’en 2016, il y avait 817 000 abonnements Internet à haut débit et à très haut débit de
plus qu’en 2015.
3. Quelle formule a-t-on pu saisir dans la cellule B4 avant de la recopier vers la droite, jusqu’à la
cellule D4?
4. En 2015, seulement 5,6 % des abonnements Internet à très haut débit utilisaient la fibre optique.
Quel nombre d’abonnements Internet à très haut débit cela représentait-il ?
EXERCICE 2 : 14 POINTS
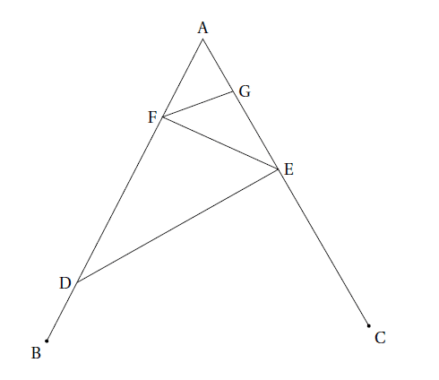
La figure ci-dessous n’est pas en vraie grandeur.
On donne les informations suivantes :
— Le triangle ADE a pour dimensions :
AD = 7 cm, AE = 4,2 cm et DE = 5,6 cm.
— F est le point de [AD] tel que AF = 2,5 cm.
— B est le point de [AD) et C est le point de [AE)
tels que : AB = AC = 9 cm.
— La droite (FG) est parallèle à la droite (DE).
1. Réaliser une figure en vraie grandeur.
2. Prouver que ADE est un triangle rectangle en E.
3. Calculer la longueur FG.
EXERCICE 3 : 15 POINTS
Deux urnes contiennent des boules numérotées indiscernables au toucher.
Le schéma ci-dessous représente le contenu de chacune des urnes.
On forme un nombre entier à deux chiffres en tirant au hasard une boule dans chaque urne :
— le chiffre des dizaines est le numéro de la boule issue de l’urne D;
— le chiffre des unités est le numéro de la boule issue de l’urne U.
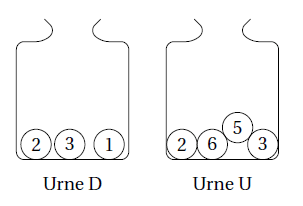
Exemple : en tirant la boule 1 de l’urne D et ensuite la boule 5 de l’urne U, on forme le
nombre 15.
1. A-t-on plus de chance de former un nombre pair que de former un nombre impair ?
2. a. Sans justifier, indiquer les nombres premiers qu’on peut former lors de cette expérience.
b. Montrer que la probabilité de former un nombre premier est égale à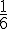 
.
3. Définir un événement dont la probabilité de réalisation est égale à .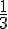
EXERCICE 4 : 14 POINTS
Dans cet exercice, aucune justification n’est attendue.
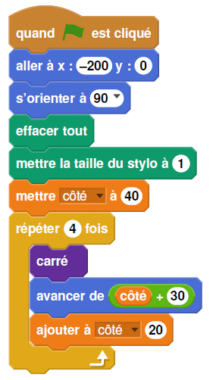
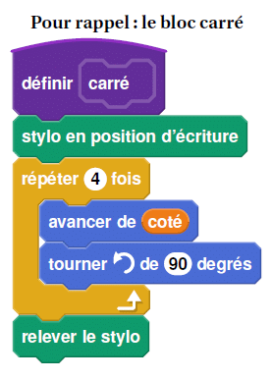
Simon travaille sur un programme. Voici des copies de son écran :
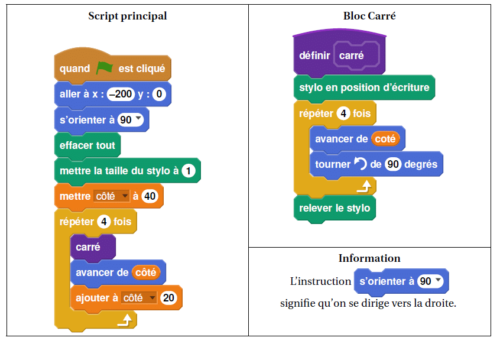
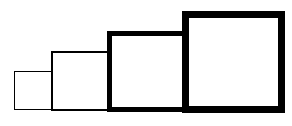
1. Il obtient le dessin ci-dessous.
a. D’après le script principal, quelle est la longueur du côté du plus petit carré dessiné?
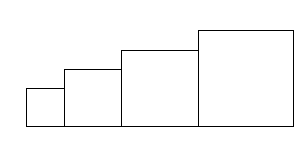
b. D’après le script principal, quelle est la longueur du côté du plus grand carré dessiné?
2. Dans le script principal, où peut-on insérer l’instruction 
ajouter 2 à la taille du stylo de façon à obtenir le dessin ci-dessous?
3. On modifie maintenant le script principal pour obtenir celui qui est présenté ci-dessous :
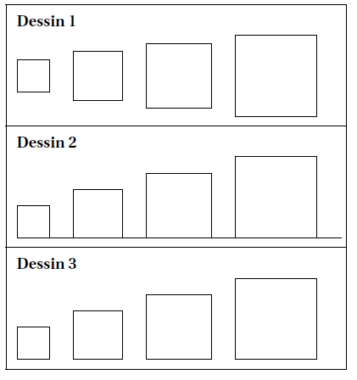
Parmi les dessins ci-dessous, lequel obtient-on?
EXERCICE 5 : 6 POINTS
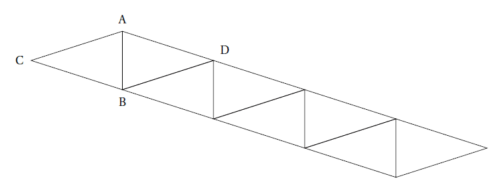
Gaspard travaille avec un logiciel de géométrie dynamique pour construire une frise.
Il a construit un triangle ABC isocèle en C (motif 1) puis il a obtenu le losange ACBD (motif 2).
Voici les captures d’écran de son travail.
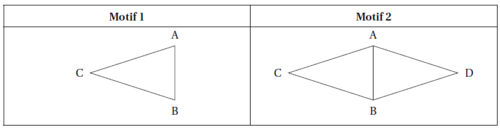
1. Préciser une transformation permettant de compléter le motif 1 pour obtenir le motif 2.
2. Une fois lemotif 2 construit, Gaspard a appliqué à plusieurs reprises une translation.
Il obtient ainsi la frise ci-dessous.
Préciser de quelle translation il s’agit.
EXERCICE 6 : 16 POINTS
Madame Martin souhaite réaliser une terrasse en béton en face de sa baie vitrée.
Elle réalise le dessin ci-dessous.
Pour faciliter l’écoulement des eaux de pluie, le sol de la terrasse doit être incliné.
La terrasse a la forme d’un prisme droit dont la base est le quadrilatère
ABCD et la hauteur est le segment [CG].
P est le point du segment [AD] tel que BCDP est un rectangle.
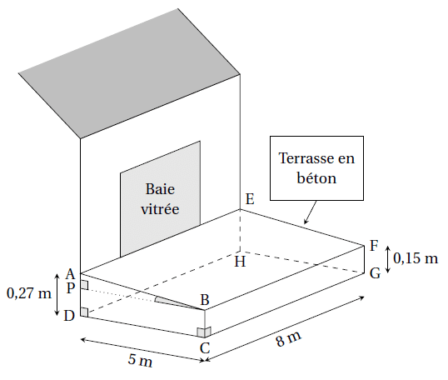
1. L’angle dABP doitmesurer entre 1° et 1,5°.
Le projet deMadameMartin vérifie-t-il cette condition?
2. MadameMartin souhaite se faire livrer le béton nécessaire à la réalisation de sa terrasse.
Elle fait appel à une entreprise spécialisée.
À l’aide des informations contenues dans le tableau ci-dessous, déterminer le montant de la
facture établie par l’entreprise.
On rappelle que toute trace de recherche, même incomplète, pourra être prise en compte dans
l’évaluation.
EXERCICE 7 : 15 POINTS
Les trois questions suivantes sont indépendantes.
1. A = 2x(x −1)−4(x −1).
Développer et réduire l’expression A.
2. Montrer que le nombre −5 est une solution de l’équation (2x +1)×(x −2) = 63.
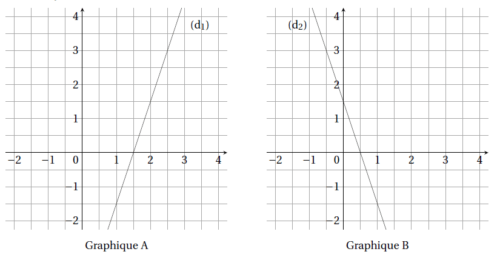
3. On considère la fonction f définie par f (x) = −3x +1,5.
a. Parmi les deux graphiques ci-dessous, quel est celui qui représente la fonction f ?
b. Justifiez votre choix.
EXERCICE 8 : 6 POINTS
On considère la fenêtre de téléchargement ci-dessous.
Si la vitesse de téléchargement reste constante, faudra-t-il plus d’une minute et vingt-cinq secondes
pour que le téléchargement se termine?
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2018 en Amérique du Nord – sujet et corrigé» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
