Brevet Maths 2022 : sujet de mathématiques du brevet en Amérique du Nord

brevet de maths Signaler une erreur / Remarque ?

BREVET  DE MATHÉMATIQUES

AMERIQUE DU NORD

Session : JUIN 2022

Durée de l’épreuve : 2 heures

Exercice 1 : 22 points.

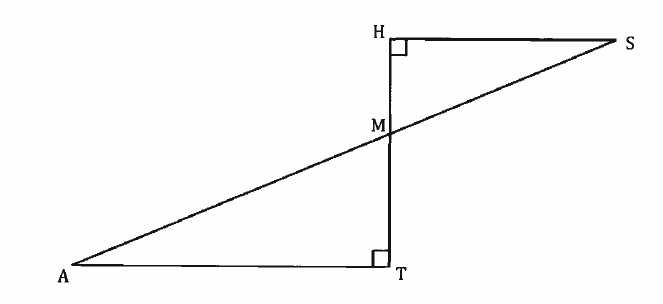
La figure ci-dessous n’est pas l’échelle.

• les points M, A et S sont alignés
• les points M, T et H sont alignés
• MH = S cm
• MS = 13 cm
• MT = 7 cm

1. Démontrer que la longueur HS est égale à 12 cm.
2. Calculer la longueur AT.
3.  Calculer la mesure de l’angle . On arrondira le résultat au degré prés.
4. Parmi les transformations suivantes quelle est celle qui permet d’obtenir le triangle MAT partir
   du triangle MHS ? Dans cette question, aucune justification n ‘est attendue. Recopier la réponse sur la copie.

5. Sachant que la longueur MT est fois plus grande que la longueur HM, un élève affirme :

«L’aire du triangle MA T est 1,4 fois plus grande que l’aire du triangle MHS »
Cette affirmation est-elle vraie ? On rappelle que la réponse doit être justifiée.

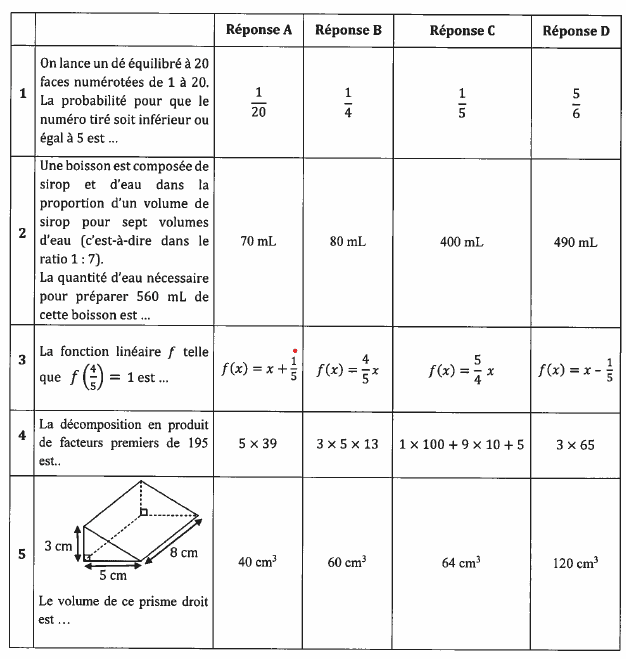
Exercice 2 : 15 points
Dans cet exercice, aucune justification n ‘est attendue.
Cet exercice est un questionnaire à choix multiple. Pour chaque question, une seule des quatre
réponses est exacte.
Sur la copie, écrire le numéro de la question et la réponse choisie.

Exercice 3 : 20 points

1. Sur les 1,6 million d’adolescents de 11 à 17 ans interrogés, combien ne respectent pas cette
recommandation ?
Après la lecture de ce communiqué, un adolescent se donne un objectif.
Objectif : « Faire au moins une heure de pratique physique par jour en moyenne. »
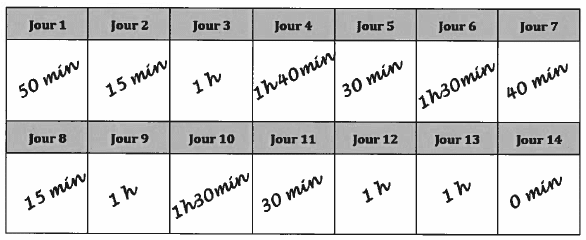
Pendant 14 jours consécutifs, il note dans le calendrier suivant, la durée quotidienne qu’il consacre
sa pratique physique :

2.a. Quelle est l’étendue des 14 durées quotidiennes notées dans le calendrier ?
b. Donner une médiane de ces 14 durées quotidiennes.
3.a. Montrer que, sur les 14 premiers jours, cet adolescent n’a pas atteint son objectif.
b. Pendant les 7 jours suivants, cet adolescent décide alors de consacrer plus de temps au sport
pour atteindre son objectif sur l’ensemble des 21 jours.
Sur ces 7 derniers jours, quelle est la durée totale de pratique physique qu’il doit au minimum
prévoir pour atteindre son objectif ?

Exercice 4 : 21 points
Dans cet exercice, aucune justification n ‘est attendue.

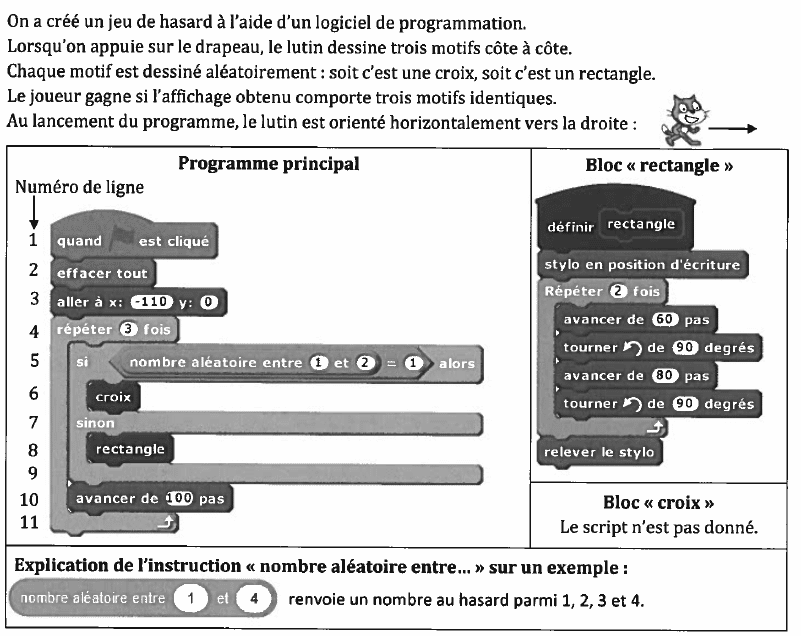
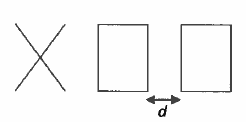
1. En prenant pour échelle 1 cm pour 20 pas, représenter le motif obtenu parle bloc « rectangle ».
2. Voici un exemple d’affichage obtenu en exécutant le programme principal :

Quelle est la distance d entre les deux rectangles sur l’affichage, exprimée en pas ?

3. Quelle est la probabilité que le premier motif dessiné par le lutin soit une croix ?
4. Dessiner à main levée les 8 affichages différents que l’on pourrait obtenir avec le programme
principal.
5. On admettra que les 8 affichages ont la même probabilité d’apparaître.
Quelle est la probabilité que le joueur gagne ?

6. On souhaite désormais que, pour chaque motif, il y ait deux fois plus de chances d’obtenir un
rectangle qu’une croix. Pour cela, il faut modifier l’instruction dans la ligne 5.
Sur la copie, recopier l’instruction suivante en complétant les cases :

Exercice 5 : 22 points
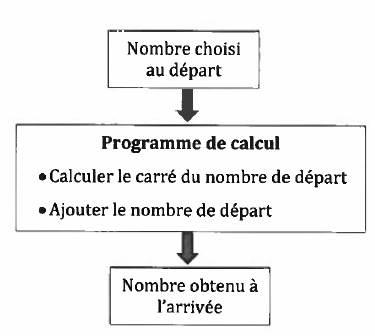
On considère le programme de calcul suivant, appliqué à des nombres entiers :

PARTIE A
1. Vérifier que si le nombre de départ est 15, alors le nombre obtenu l’arrivée est 240.

2. Voici un tableau de valeurs réalisé l’aide d’un tableur :
II donne les résultats obtenus par le programme de calcul en fonction de quelques valeurs du nombre choisi au départ.
Quelle formule a pu être saisie dans la cellule B2 avant d’être étirée vers le bas ?
Aucune justification n ‘est attendue.
3. On note x le nombre de départ.
Écrire, en fonction de x, une expression du résultat obtenu avec ce programme de calcul.

PARTIE B
On considère l’affirmation suivante :

« Pour obtenir le résultat du programme de calcul, il suffit de multiplier le nombre de départ
par le nombre entier qui suit. »
4.  Vérifier que cette affirmation est vraie lorsque le nombre entier choisi au départ est 9.
5. Démontrer que cette affirmation est vraie quel que soit le nombre entier choisi au départ.
6. Démontrer que le nombre obtenu l’arrivée par le programme de calcul est un nombre pair
quel que soit le nombre entier choisi au départ.

 Consulter le corrigé en ligne

Cette publication est également disponible en : English (Anglais) Español (Espagnol) العربية (Arabe)

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet Maths 2022 : sujet de mathématiques du brevet en Amérique du Nord» au format PDF.

• Brevet Maths 2022 en France : sujet et corrigé du brevet
• Polynésie Française : brevet de maths 2022 avec sujet et corrigé
• Asie et Pacifique : brevet de maths 2022 avec sujet et corrigé
• Brevet Maths 2021 : sujet et corrigé du brevet blanc de maths
• Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
• Brevet Maths 2021 : sujet blanc pour réviser le brevet
• Brevet de maths 2022 aux centres étrangers : sujet et corrigé du brevet.
• Brevet de maths 2017 : sujet blanc
• Brevet de maths 2017 sujet 0
• Sujet du brevet de maths France 2016

 Mathovore c'est 13 624 708 cours et exercices de maths téléchargés en PDF.