Sections de solides : cours de maths en 3ème à télécharger en PDF.

Sommaire de cette fiche

1 I.Formules des aires de figures et volumes de solides :
- 1.1 1.Formules des aires de figures :
- 1.2 2.Formulaire des volumes de solides :
2 II. Sections planes de surfaces :
3 III. Les agrandissements et les réductions de solides :

Un cours de maths en 3ème sur les volumes de solides et les sections de solides dans l’espace. Nous aborderons dans cette leçon différents rappels sur les aires de figures (rectangle, parallélogramme, trapèze) puis les formules de calculs du volume d’une pyramide, d’un cylindre de révolution ou encore, d’une boule. Puis, dans un second temps, nous effectuerons des sections de solides par un plan et nous effectuerons des calculs avec les notions de réduction et d’agrandissement.

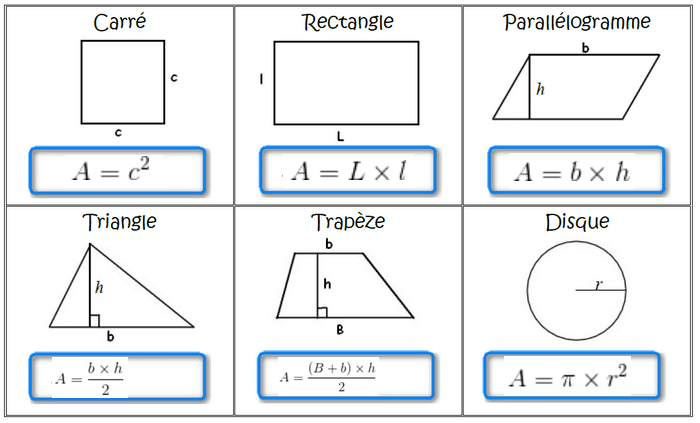
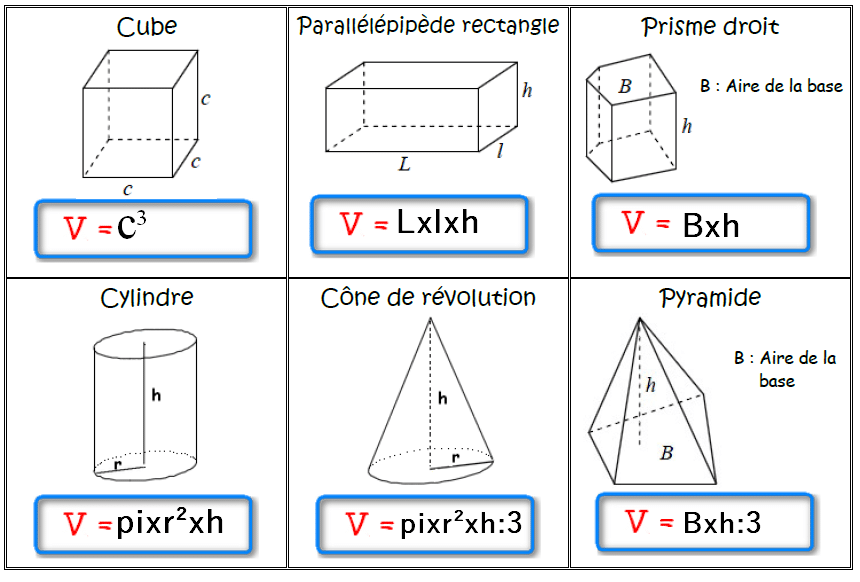
I.Formules des aires de figures et volumes de solides :

1.Formules des aires de figures :

2.Formulaire des volumes de solides :

II. Sections planes de surfaces :

Définition :

En géométrie, on appelle section plane l’intersection entre un solide et un plan.

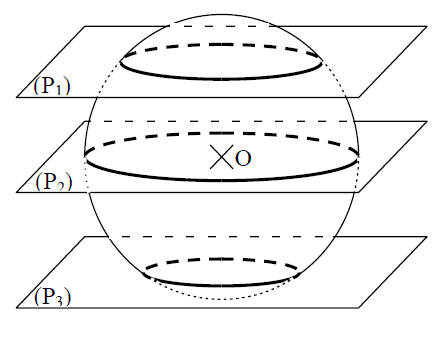
1. Section d’une boule par un plan :

Propriété :

La section d’une boule par un plan est un disque .
Lorsque le plan passe par le centre de la boule, la section est un disque de même centre et de même rayon.

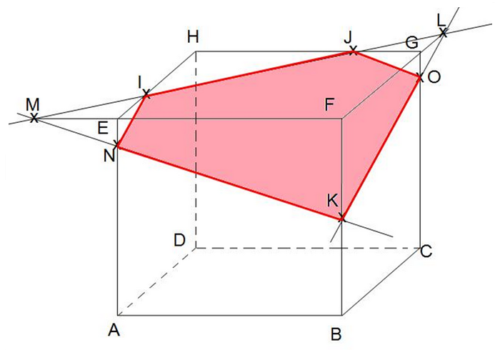
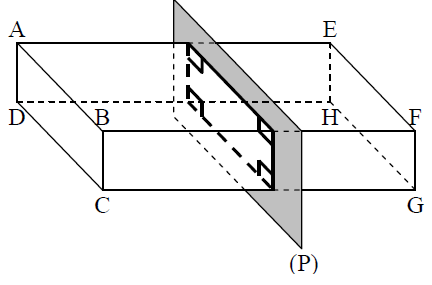
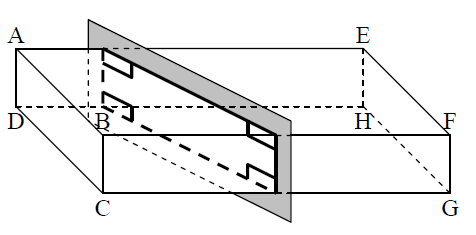
2.Section d’un pavé droit par un plan

Propriété :

La section d’un pavé droit par un plan parallèle à une face est un rectangle.

Propriété :

La section d’un pavé droit par un plan parallèle à une arête est un rectangle.

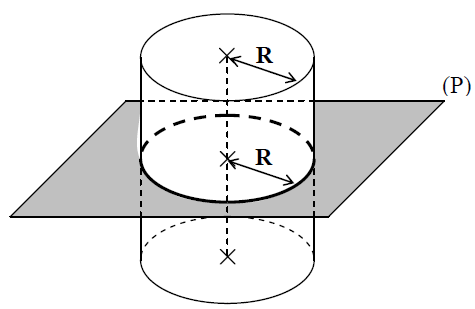
3.Section d’un cylindre de révolution par un plan :

Propriété :

La section d’un cylindre de révolution de rayon R par un plan parallèle aux bases est un disque de rayon R.

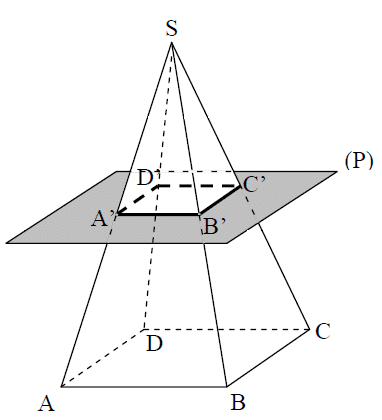
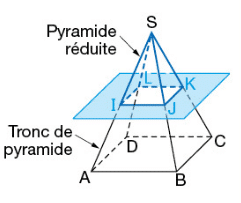
4.Section d’une pyramide par un plan :

Propriété :

La section d’une pyramide par un plan parallèle à la base est un polygone ayant la
même forme que la base.

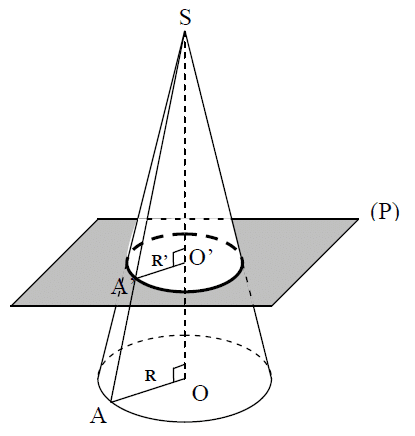
5.Section d’un cône de révolution par un plan :

Propriété :

La section d’un cône de révolution par un plan parallèle à la base est un disque dont le centre appartient à la hauteur de ce cône.

III. Les agrandissements et les réductions de solides :

Définition :

Considérons une section plane parallèlement à une base.Nous obtenons une réduction (ou un agrandissement) du solide.
Lorsque deux figures ont la même forme, on peut calculer le coefficient suivant :
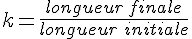Le coefficient de réduction, noté k, est donné par la formule : $k=\frac{longueur\,finale}{longueur\,\,initiale}$

>0.

Propriété :

Considérons un agrandissement (ou une réduction) de rapport k.

Si 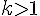alors c’est un agrandissement;
Si 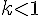alors c’est une réduction.

Propriété :

Lors d’un agrandissement (ou d’une réduction) de rapport k :

les longueurs sont multipliées par k ;
les aires sont multipliées par ;
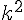les volumes sont multipliés par .

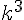Exemple :

On considère la pyramide de base ABCD et la section IJKL effectuée parallèlement à sa base.

Nous savons que SJ= 6 cm; SB = 10 cm; 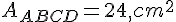$A_{ABCD}=24_,cm^2$ .

Calculer l’aire de la section IJKL.

Le coefficient de réduction est 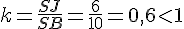$k=\frac{SJ}{SB}=\frac{6}{10}=0,6<1$ .

Nous avons :

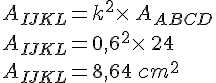
$A_{IJKL}=k^2\times \,A_{ABCD}\\A_{IJKL}=0,6^2\times \,24\,\\A_{IJKL}=8,64\,cm^2$

4.1/5 - (48 votes)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «sections planes de solides : cours de maths en 3ème» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés.

D'autres fiches similaires à sections planes de solides : cours de maths en 3ème.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à sections planes de solides : cours de maths en 3ème à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème sections planes de solides : cours de maths en 3ème, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Sections de solides : cours de maths en 3ème
58
Les sections de solides dans l'espace dans un cours de maths en 3ème où nous aborderons la réduction et l'agrandissement de figures géométriques dans l'espace. Nous étudierons dans cette leçon en troisième, les sections de cônes, de pyramides, de cubes ou encore de boules. I.Section d'un prisme droit par un…

Les dernières fiches mises à jour

Voici les dernières ressources mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 2 365 080 cours et exercices de maths téléchargés en PDF et 181 073 membres.
Rejoignez-nous : inscription gratuite.