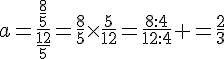Fonctions linéaires : corrigé des exercices de maths en 3ème en PDF.

Mis à jour le 28 mai 2025

🔍Corrigés Détaillés

3eme • Scolaire

Fonctions linéaires

🔎 Analyse : 15 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en 3ème sur les fonctions linéaires.

Calculer des images et des antécédents. Travailler sur la courbe d’une fonction linéaire et exploitation de tableau de valeurs.

Exercice 1 :
Soit la fonction linéaire f : x 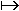1,2x.

a. Calculer f(5) ; f(- 1,2) ; f(0) ; f(100).

f(5)=1,2×5=6 ; f(-1,2)=- 1,44 ; f(0)= 0 ; f(100 ) = 120

b. Calculer les nombres x dont les images sont 2 400 ; – 45.

$x=\frac{2400}{1,2}=200$

$x=\frac{-45}{1,2}=-37,5$

Exercice 2 :
Soit g la fonction linéaire telle que g 😡 – 0,4x.

a. Quel est le coefficient de la fonction g ?

a = – 0,4

b. Calculer les images de 10 ; – 5 et 1.

g(10) = – 4 ; g(-5)=2 ; g(1) = -0,4

Exercice 3 :
On sait que 18 a pour image 23 par la fonction f et que 12 a pour image 14 par f.

f est-elle une fonction linéaire ?Pourquoi ?

Comparons $\frac{23}{18}$ et $\frac{14}{12}$ :

$23\times 12=276\,\,14\times 18=252$

Les fractions ne sont pas égales donc ce n’est pas une fonction linéaire .

Exercice 4 :

Exprimer la fonction linéaire f sous la forme $x\mapsto \,\,\,ax$ ( le nombre a est à déterminer), puis calculer f(0) ; f(1) et f( – 2).

1. Lorsque l’image de 10 est – 3.

Nous avons $a=-\frac{3}{10}=-0,3$ donc f est telle que .

2. Lorsque f (- 100)= – 46.
Nous avons $a=\frac{-46}{-100}=0,46$ donc f est telle que .

3. Lorsque le coefficient de f est 2,5.
Nous avons f qui est définie par .

Exercice 5 :

Dans un repère, il suffit de connaître les coordonnées d’un seul point ( dont l’abscisse est non nul) appartenant à la courbe d’une fonction linéaire pour la tracer.

a. Pour $f:x\,\mapsto \,\,\,2,5x$ .

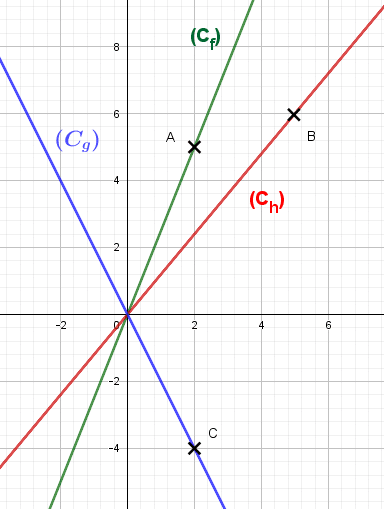
Nous avons f(2)=2,5×2 = 5 donc la courbe passe par le point A(2;5).

b. Tracer la droite d d’équation y = 1,2x, nous noterons cette fonction h.
Nous avons h(5)=1,2×5=6 donc la courbe passe par le point B ( 5 ; 6).

c. Tracer la droite d’ représentant la fonction linéaire g de coefficient a = – 2.

Nous avons g(1)= – 2 donc la courbe passe par C(1;- 2).

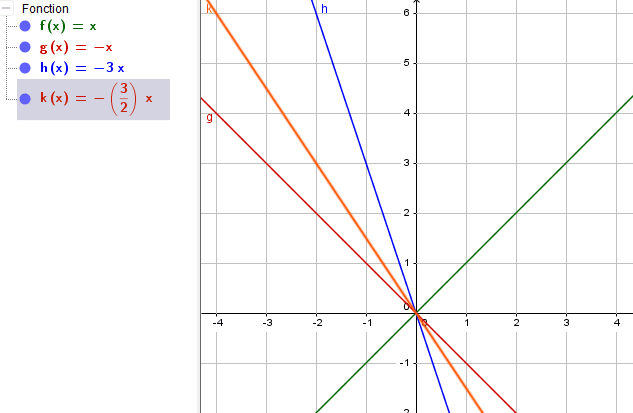
Voici les courbes de ces trois fonctions linéaires :

Exercice 10 :
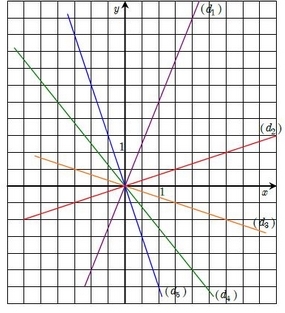
Voici les courbes de ces cinq fonctions linéaires.

y=2,5x est (d1)

y= – 3x est (d5)

$y=-\frac{1}{3}x$ ets (d3)

$y=\frac{1}{3}x$ est (d2)

$y=-\frac{5}{4}x$ est (d4)

Exercice 14 :

f est une fonction linéaire . Déterminer l’expression de f(x)

$f(\frac{12}{5})=\frac{8}{5}$

f est du type .

$f(\frac{12}{5})=a\times \frac{12}{5}=\frac{8}{5}$

$a=\frac{\frac{8}{5}}{\frac{12}{5}}=\frac{8}{5}\times \frac{5}{12}=\frac{8:4}{12:4} =\frac{2}{3}$

Conclusion : ${\color{DarkRed} f(x)=\frac{2}{3}x}$

Exercice 15 :

a) Soit : x le prix initial d’un article et : y son prix final après une augmentation ou une baisse. Quel est le pourcentage d’augmentation ou de baisse dans chacun des cas suivants ? (1): y = 1.4x

$1,4=1+0,4=1+\frac{40}{100}$

C’est une augmentation de 40 % .

(2): y = 0.5x

$0,5=1-0,5=1-\frac{50}{100}$

C’est une réduction de 50 % .

(3): y = 0.9x

$0,9=1-0,1=1-\frac{10}{100}$

C’est une réduction de 10 % .

(4): y = 1.05x

$1,05=1+0,05=1+\frac{5}{100}$

C’est une augmentation de 5 % .

Exercice 16 :

1. Un objet A coûte 65 euros. Son prix augmente de 5%.

Combien coûte-t-il après cette augmentation?

Le coefficient multiplicateur est $k=1+\frac{5}{100}=1,05$ .

$65\times 1,05=68,25$

Le prix final est de 68,25 euros .

2.Un objet B coûte 88 euros après une augmentation de 10%.

Quel était son prix avant cette augmentation?

Le coefficient multiplicateur est $k=1+\frac{10}{100}=1,1$ .

$\frac{88}{1,1}=80$

Le prix avant augmentation est de 80 euros .

3.Un objet C coûte 45 euros. Après une augmentation son prix est de 50,40 euros.

Quel est le pourcentage de cette augmentation?

Le coefficient multiplicateur est $k=\frac{50,40}{45}=1,12=1+0,12=1+\frac{12}{100}$

L’augmentation était de 12 % .

Exercice 17 :

Un gérant de magasin de vêtements décide de baisser ses prix de 15 % .

a) Quelle est la fonction linéaire modélisant cette baisse ?

La fonction linéaire modélisant une baisse de 15 % est f(x)=0,85x .

b) Quelle est le nouveau prix d’un pantalon qui coûtait 70 e avant cette baisse ?

f(70)=0,85×70=59,5 €

c) Quel est l’ancien prix d’un pull qui coûte 50,12 € après cette baisse ?

On cherche x tel que f(x)=50,12

d’où 0,85x=50,12

$x=\frac{50,12}{0,85}$

soit

Conclusion : l’ancien prix du pull était de 56 € .

Exercice 18 :

On considère la fonction linéaire f de coefficient – 5.

Nous avons donc f(x)= – 5x

Calculer l’image par f des nombres suivants :

a) 0

f(0)=0 (f est une fonction linéaire).

b) 3

$f(3)=-5\times 3=-15$

c) – 2

$f(-2)=-5\times (-2)=10$

d) $\frac{3}{7}$

$f(\frac{3}{7})=-5\times (\frac{3}{7})=-\frac{15}{7}$

e) $-\sqrt{3}$

$f(-\sqrt{3})=-5\times (-\sqrt{3})=5\sqrt{3}$

Exercice 19 :

Pour chaque fonction, préciser si elle est linéaire et, dans ce cas, son coefficient.

a) $f:x \mapsto 3,5x$

Elle est linéaire de coefficient a= 3,5 .

b) $g:x \mapsto 2+x$

elle n’est pas linéaire, c’est une fonction affine.

c) $h:x \mapsto 7x^2$

elle n’est pas linéaire, c’est une fonction carrée.

d) $i:x \mapsto -x$

elle est linéaire de coefficient a= – 1 .

e) $j:x \mapsto 5$

elle n’est pas linéaire , c’est une fonction constante .

f) $k:x \mapsto \frac{5x}{3}$

elle est linéaire de coefficient $a=\frac{5}{3}$ .

Exercice 20 :

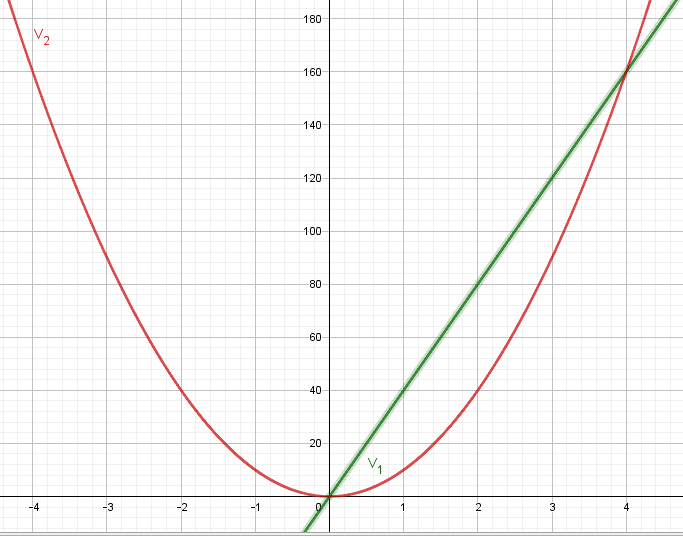
Un produit de facteurs est nul si et seulement si l’un des facteurs au moins est nul.

$x=0\,\,ou\,\,x-4=0$

$x=0\,\,ou\,\,x=4$

Conclusion : Les nombres 0 et 4 ont la même image par V1 et V2 .

Exercice 21 :

Soit f la fonction linéaire définie par : $f: x \mapsto -2x$ .

1. Calculer f(3), f( – 2), f(7).

$f(3)=-2\times 3=-6$

$f(-2)=-2\times (-2)=4$

$f(7)=-2\times 7=-14$

2. Quelles sont les images par f de – 1, 6, $\frac{3}{2}$ ?

$f(-1)=-2\times (-1)=2$

$f(6)=-2\times 6=-12$

$f(\frac{3}{2})=-2\times \frac{3}{2}=-3$

3. Trouver le nombre qui a pour image 7.

$x=-\frac{7}{2}$

${\color{DarkRed} x=-3,5}$

Les fonctions linéaires sont très utiles et intéressantes car elles vous permettent de développer des compétences.

Exercice 22 :

Compléter le tableau suivant donnant les images des nombres –1,5 , – $\frac{1}{2}$ , 0 , 1, $\frac{3}{4}$ , et 2 par chacune des applications linéaires proposées.

	–1,5	– $\frac{1}{2}$	1	$\frac{3}{4}$	2
x $\mapsto$ 3x	-4,5	-1,5	3	2,25	6
X $\mapsto$ -2x	3	1	-2	-1,5	-4
X $\mapsto$ $\frac{,1}{4}$ x	-0,375	-0,125	0,25	0,1875	0,5
X $\mapsto$ – $\frac{3}{4}$ x	1,125	0,375	-0,75	-0,5625	-1,5
X $\mapsto$ 0,3x	-0,45	-0,15	0,3	0,225	0,6

Exercice 23 :

Indiquer pour chacun des tableaux, s’il s’agit d’un tableau de proportionnalité et, si c’est le cas, exprimer l’application linéaire associée, traduisant la correspondance entre la première et la seconde ligne.

Tableau 1 : NON car $\frac{10}{5}\neq \frac{15}{10}$ .

Tableau 2 : Oui le coefficient de proportionnalité est $a=\frac{1}{3}$ .

Tableau 3 : Oui le coefficient de proportionnalité est .

Tableau 4 : Non car $4\times 7=28\neq 35$ .

Tableau 1				Tableau 3
5	10	15	20	1,5	2	2,5	3
10	15	20	25	4,5	6	7,5	9
Tableau 2				Tableau 4
30	33	36	39	7	14	21	35
10	11	12	13	1	2	3	4

Exercice 24 :

Dans chacun des cas, on connaît un nombre et son image par une application linéaire. Déterminer son coefficient et l’exprimer sous la forme la plus simple possible.

8 $\mapsto$ – 64

$a=-\frac{64}{8}=-8$

9 $\mapsto$ 6

$a=\frac{6}{9}=\frac{2}{3}$

7 $\mapsto$ 4,9

$a=\frac{4,9}{7}=0,7$

11 $\mapsto$ -32

$a=-\frac{32}{11}$

0,3 $\mapsto$ 12

$a=\frac{12}{0,3}=40$

1,2 $\mapsto$ 0,4

$a=\frac{0,4}{1,2}=\frac{1}{3}$

; – 2,5 $\mapsto$ – 8

$a=\frac{8}{2,5}=31,2$

25 $\mapsto$ – 5

$a=\frac{-5}{25}=-\frac{1}{5}$

Exercice 25 :

Compléter les tableaux de valeurs des applications linéaires en utilisant les propriétés de la linéarité.

Application 1					Application 2
3	36	18	4	-2	2	4	-4	10	-12
10,5	126	63	14	-7	2,5	5	-5	12,5	-15

Exercice 26 :

Donner les applications linéaires associées aux situations suivantes utilisant des pourcentages :

Augmenter de 25% $f:x\,\mapsto \,(1+\frac{25}{100})x=1,25x$
Diminuer de 20% $f:x \mapsto 0,8x$
Diminuer de 4% $f:x\,\mapsto \,0,96x$
Augmenter de 10% $f:x\,\mapsto \,1,1x$
Diminuer de 75% $f:x\,\mapsto \,0,25x$

Exercice 27 :

Traduire chacune de ces applications linéaires par une variation en pourcentage :

x $\mapsto$ 1,35x (+35%)	x $\mapsto$ 0,98x (- 2%)	x $\mapsto$ 3/2 x (+ 50%)	x $\mapsto$ ¾ x (-25%)	x $\mapsto$ 1,01 x (+ 1%)
x $\mapsto$ 0,86x (-14 %)	x $\mapsto$ 1,31x (+ 31 %)	x $\mapsto$ 4/9 x (-55,5%)	x $\mapsto$ 5/8 x (-37,5 %)	x $\mapsto$ 1,002x (+ 0,2 %)

Exercice 28 :

Les points suivants dont on donne les cordonnées sont-ils situés sur la droite représentant graphiquement l’application linéaire x $\mapsto$ – 0,75x ?

A (-1 ; 0,75) B (-2 ; $\frac{3}{2}$ ) C (-0,2 ; – 0,15) D (- $\frac{4}{3}$ ; 1)

$f(-1)=-0,75\times \,(-1)=0,75$ Oui pour A.

$f(-2)=-0,75\times \,(-2)=1,5=\frac{3}{2}$ Oui pour B.

$f(-0,2)=-0,75\times \,(-0,2)=0,15$ Non pour C.

$f(-\frac{4}{3})=-0,75\times \,(-\frac{4}{3})=-\frac{3}{4}\times \,(-\frac{4}{3})=1$ Oui pour C.

Exercice 29 :

Dans un même repère représenter graphiquement les applications linéaires définies par :

x $\mapsto$ x ; x $\mapsto$ – x ; x $\mapsto$ – 3x ; x $\mapsto$ – $\frac{3}{2}$ x

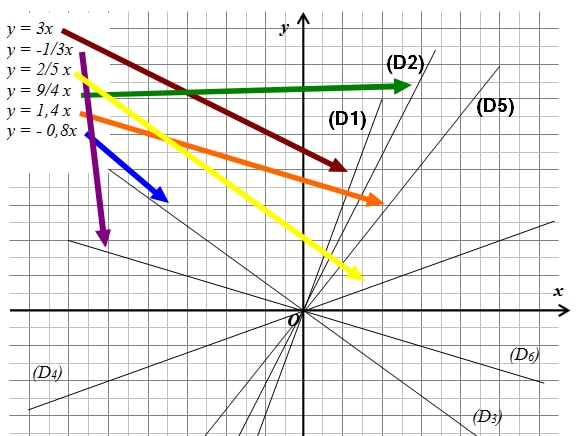
Exercice 30 :

Associer chacune des droites représentées à l’une des applications linéaires proposées.

4.4/5 - (27897 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonctions linéaires : corrigé des exercices de maths en 3ème en PDF.» au format PDF.

Ressources de troisième

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Fonctions linéaires : corrigé des exercices de maths en 3ème en PDF.

Ressources de troisième

Cours de troisième

Exercices de troisième

Brevet

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques