France 2017 : sujet du brevet de maths avec son corrigé

DIPLÔME NATIONAL DU BREVET SESSION 2017
PREMIÈRE ÉPREUVE

1ère partie
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 heures – 50 points

THÉMATIQUE COMMUNE DE L’ÉPREUVE DE MATHÉMATIQUES-SCIENCES : L’ÉNERGIE

Exercice 1 (4 points)
Dans une urne contenant des boules vertes et des boules bleues, on tire au hasard une boule et on regarde sa couleur. On replace ensuite la boule dans l’urne et on mélange les boules.
La probabilité d’obtenir une boule verte est $\frac{2}{5}$ .
1. Expliquer pourquoi la probabilité d’obtenir une boule bleue est égale à $\frac{3}{5}$ .
2. Paul a effectué 6 tirages et a obtenu une boule verte à chaque fois.
Au 7e tirage, aura-t-il plus de chances d’obtenir une boule bleue qu’une boule verte ?
3. Déterminer le nombre de boules bleues dans cette urne sachant qu’il y a 8 boules vertes.

Exercice 2 (6 points)
On donne le programme suivant qui permet de tracer plusieurs triangles équilatéraux de tailles différentes.
Ce programme comporte une variable nommée « côté ». Les longueurs sont données en pixels.
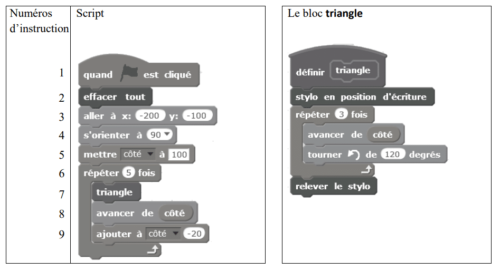
On rappelle que l’instruction signifie que l’on se dirige vers la droite.

1. Quelles sont les coordonnées du point de départ du tracé ?
2. Combien de triangles sont dessinés par le script ?

3. a. Quelle est la longueur (en pixels) du côté du deuxième triangle tracé ?
b. Tracer à main levée l’allure de la figure obtenue quand on exécute ce script.
4. On modifie le script initial pour obtenir la figure ci-dessous.

Indiquer le numéro d’une instruction du script après laquelle on peut placer
l’instruction pour obtenir cette nouvelle figure.

Exercice 3 (4 points)
Un condensateur est un composant électronique qui permet de stocker de l’énergie électrique pour la restituer plus tard.
Le graphique suivant montre l’évolution de la tension mesurée aux bornes d’un condensateur en fonction du temps lorsqu’il est en charge.
1. S’agit-il d’une situation de proportionnalité ? Justifier.
2. Quelle est la tension mesurée au bout de 0,2 s ?
3. Au bout de combien de temps la tension aux bornes du condensateur aura-t-elle atteint 60% de la tension maximale qui est estimée à 5 V ?

Exercice 4 (8 points)
Les panneaux photovoltaïques permettent de produire de l’électricité à partir du rayonnement solaire.
Une unité courante pour mesurer l’énergie électrique est le kilowatt-heure, abrégé en kWh.
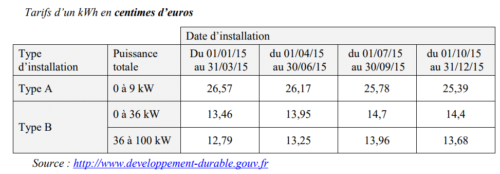
1. Le plus souvent, l’électricité produite n’est pas utilisée directement, mais vendue pour être distribuée dans le réseau électrique collectif. Le prix d’achat du kWh, donné en centimes d’euros, dépend du type
d’installation et de sa puissance totale, ainsi que de la date d’installation des panneaux photovoltaïques. Ce prix d’achat du kWh est donné dans le tableau ci-dessous.

En mai 2015, on installe une centrale solaire du type B, d’une puissance de 28 kW.
Vérifier que le prix d’achat de 31 420 kWh est d’environ 4 383 €.

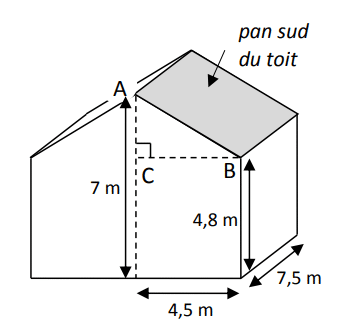
2. Une personne souhaite installer des panneaux photovoltaïques sur la partie du toit de sa maison orientée au sud. Cette partie est grisée sur la figure ci-contre. Elle est appelée pan sud du toit.
La production d’électricité des panneaux solaires dépend de l’inclinaison du toit.
Déterminer, au degré près, l’angle $\widehat{ABC}$ que forme ce pan sud du toit avec l’horizontale.

3. a. Montrer que la longueur AB est environ égale à 5 m.
b. Les panneaux photovoltaïques ont la forme d’un carré de 1 m de côté.
Le propriétaire prévoit d’installer 20 panneaux.
Quel pourcentage de la surface totale du pan sud du toit sera alors couvert par les panneaux solaires ? On donnera une valeur approchée du résultat à 1% près.
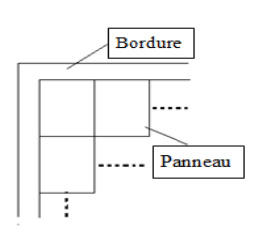
c. La notice d’installation indique que les panneaux doivent être accolés les uns aux autres et qu’une bordure d’au moins 30 cm de large doit être laissée libre pour le système de fixation tout autour de l’ensemble des panneaux.
Le propriétaire peut-il installer les 20 panneaux prévus ?

Exercice 5 (8 points)
1. Lors des Jeux Olympiques de Rio en 2016, la danoise Pernille Blume a remporté le 50 m nage libre en 24,07 secondes.
A-t-elle nagé plus rapidement qu’une personne qui se déplace en marchant vite, c’est-à-dire à 6 km/h ?
2. On donne l’expression
a. Développer E.
b. Montrer que E peut s’écrire sous forme factorisée :.
c. Résoudre l’équation
3. La distance de freinage d’un véhicule dépend de sa vitesse et de l’état de la route.
On peut la calculer à l’aide de la formule suivante :
$d=k\times ,V^2$ avec d : distance de freinage en m , V: vitesse du véhicule en m/s, k: coefficient dépendant de l’état de la route.
k= 0,14 sur route mouillée
k = 0,08 sur route sèche.
Quelle est la vitesse d’un véhicule dont la distance de freinage sur route mouillée est égale à 15 m ?

Exercice 6 (8 points)

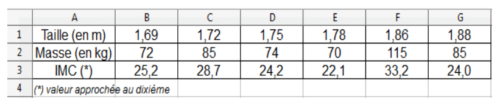
1. Dans une entreprise, lors d’une visite médicale, un médecin calcule l’IMC de six des employés.
Il utilise pour cela une feuille de tableur dont voici un extrait :

a. Combien d’employés sont en situation de surpoids ou d’obésité dans cette entreprise ?
b. Laquelle de ces formules a-t-on écrite dans la cellule B3, puis recopiée à droite, pour calculer l’IMC ?
Recopier la formule correcte sur la copie.

2. Le médecin a fait le bilan de l’IMC de chacun des 41 employés de cette entreprise. Il a reporté les
informations recueillies dans le tableau suivant dans lequel les IMC ont été arrondis à l’unité près.

a. Calculer une valeur approchée, arrondie à l’entier près, de l’IMC moyen des employés de cette
entreprise.
b. Quel est l’IMC médian ? Interpréter ce résultat.
c. On lit sur certains magazines : « On estime qu’au moins 5 % de la population mondiale est en surpoids
ou est obèse ». Est-ce le cas pour les employés de cette entreprise ?

Exercice 7 (7 points)
Léo a ramassé des fraises pour faire de la confiture.
1. Il utilise les proportions de sa grand-mère : 700 g de sucre pour 1 kg de fraises.
Il a ramassé 1,8 kg de fraises. De quelle quantité de sucre a-t-il besoin ?
2. Après cuisson, Léo a obtenu 2,7 litres de confiture.
Il verse la confiture dans des pots cylindriques de 6 cm de diamètre et de 12 cm de haut, qu’il remplit jusqu’à 1 cm du bord supérieur.
Combien pourra-t-il remplir de pots ?

Rappels : 1 litre = 1000

Volume d’un cylindre = $\pi\times ,R^2\times ,h$
3. Il colle ensuite sur ses pots une étiquette rectangulaire de fond blanc qui recouvre toute la surface latérale du
pot.
a. Montrer que la longueur de l’étiquette est d’environ 18,8 cm.
b. Dessiner l’étiquette à l’échelle $\frac{1}{3}$ .

Corrigé gratuit du sujet du brevet 2017 en France

Vous pouvez télécharger le sujet du brevet de maths 2017 en France au format PDF.

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «france 2017 : sujet du brevet de maths avec son corrigé» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 081 120 cours et exercices de maths téléchargés en PDF.