Le produit scalaire : cours de maths en terminale en PDF.

Mis à jour le 29 juin 2025

Sommaire

🧮Cours de Mathématiques

Terminale • Lycée

Le produit scalaire

📖 Temps de lecture : 5 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Le produit scalaire dans le plan dans un cours de maths en terminale et dans l’espace.
Cette leçon sur le produit scalaire est à télécharger en PDF gratuitement afin de progresser et développer vos compétences en classe de terminale.

I. Différentes expressions du produit scalaire :

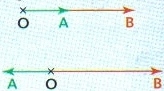
1. Vecteurs colinéaires :

Définition :

soient $\vec{u}$ et $\vec{v}$ deux vecteurs colinéaires non nuls, tels que

$\vec{u}=\vec{OA}$ et $\vec{v}=\vec{OB}$ .

• Si $\vec{u}$ et $\vec{v}$ sont de même sens : $\vec{u}.\vec{v}=OA\times OB$ .

• Si $\vec{u}$ et $\vec{u}$ sont de sens contraires : $\vec{u}.\vec{v}=OA\times OB$ .

• Si $\vec{u}=\vec{0}$ ou $\vec{v}=\vec{0}$ alors $\vec{u}.\vec{v}=0$ .

• $\vec{u}.\vec{u}=||\vec{u}||$ est le carré scalaire du vecteur $\vec{u}$

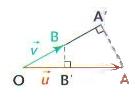
2. Vecteurs quelconques :

Propriété 1 :

Soient $\vec{u}$ et $\vec{v}$ deux vecteurs non nuls tels que

$\vec{u}=\vec{OA}$ et $\vec{v}=\vec{OB}$ .

Alors :

$\fbox{\vec{u}.\vec{v}=OA'\times OB=OA\times OB'}$ .

A’ et B’ sont respectivement les projetés orthogonaux de A sur (OB) et de B sur (OA).

3. Propriétés :

Propriété 2 :

Soient (x;y) et (x’;y’) les coordonnées respectives des vecteurs $\vec{u}$ et $\vec{v}$ dans un repere orthonormé quelconque.
$\fbox{\vec{u}.\vec{v}\,=\,x.x'+y.y'}$ .

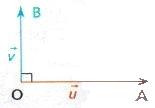
II. Produit scalaire et orthogonalité :

Définition :

Dire que $\vec{u}$ et $\vec{v}$ sont deux vecteurs orthogonaux signifie que :

• Soit $\vec{u}=\vec{0}$ ou $\vec{v}=\vec{0}$ ;

• Soit (OA) $\perp$ (OB), avec $\vec{u}=\vec{OA}$ et $\vec{v}=\vec{OB}$ non nuls.

2. Propriété :

Propriété :

$\fbox{\vec{u}\perp\vec{v}\,\,\Longleftrightarrow\,\,\vec{u}.\vec{v}=0}$

III. Propriétés du produit scalaire :

Propriétés :

Soient $,\vec{u}\,,\,\vec{v},\,\vec{w}$ trois vecteurs et k un nombre réel.

• $\vec{u}.\vec{v}=\vec{v}.\vec{u}$ (symétrie).

• $(k\vec{u}).\vec{v}=\vec{u}.(k\vec{v})=k(\vec{u}.\vec{v})$ (linéarité)

• $(\vec{u}+\vec{v}).\vec{w}=\vec{u}.\vec{w}+\vec{v}.\vec{w}$ (linéarité)

• $\vec{u}.(\vec{v}+\vec{w})=\vec{u}.\vec{v}+\vec{u}.\vec{w}$ (linéarité)

• $(\vec{u}+\vec{v})^2=\vec{u}^2+2\vec{u}.\vec{v}+\vec{v}^2$ (identité remarquable)

• $(\vec{u}-\vec{v})^2=\vec{u}^2-2\vec{u}.\vec{v}+\vec{v}^2$ (identité remarquable)

• $(\vec{u}-\vec{v})(\vec{u}+\vec{v})=\vec{u}^2-\vec{v}^2$ (identité remarquable)

IV. Applications du produit scalaire :

1. produit scalaire et cosinus :

Propriété :

Soit $\vec{u}$ et $\vec{v}$ non nuls.

$\vec{u}.\vec{v}=||\vec{u}||\times ||\vec{v}||\times cos(\vec{u},\vec{v})$

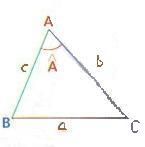
2. Théorème d’Al-Kashi :

Théorème :

Soit ABC un triangle tel que AB=c, AC=b et BC=a.

On a :

• $a^2\,=\,b^2+c^2-2bc\times cosA$

• $b^2\,=\,a^2+c^2-2ac\times cosB$

• $c^2\,=\,a^2+b^2-2ab\times cosC$

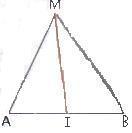
3. Théorème de la médiane :

Théorème :

Soient A et B deux points distincts et I le milieu du segment [AB] .

Pour tout point M, :

$\fbox{ MA^2\,+MB^2\,=\,2MI^2\,+\,\frac{AB^2}{2}}$

4.6/5 - (28990 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «le produit scalaire : cours de maths en terminale en PDF.» au format PDF.

Ressources de terminale

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.