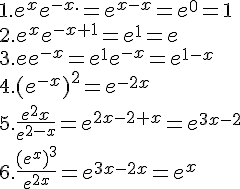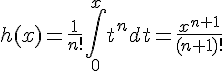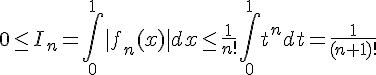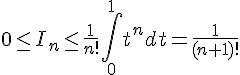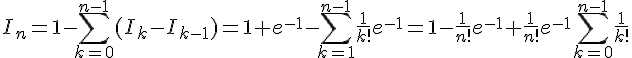Fonction exponentielle : corrigé des exercices de maths en terminale en PDF.
Mis à jour le 18 septembre 2025
Exercice 1 :
Soit la fonction f définie par
1. Donner le domaine de définition de la fonction f.
nous avons
donc pour que f soit définie, il faut que x-3>0 soit x>3.
ainsi :
2. Donner une primitive de la fonction.
les primitives de f sont de la forme :
Exercice 2 :
soit la fonction f tel que :
1. Indiquer le domaine de définition de f et transformer l’écriture du réel f(x).
donc
2. Donner un prolongement par continuité de f au point 0.
3. Etudier la dérivabilité de f au point 0.
4. Calculer la dérivée de f et étudier son signe. Etablir le tableau de variations.
5. Décrire comment se présente la tangente en ce point.
6. Construire la courbe dans un repère approprié.
Exercice 3 :
1. Démontrer que pour tout réel x, .
d’après la formule ci-dessus :
donc
car
2. Démontrer que pour tout réel x et pour tout entier naturel n,
Exercice 4:
Résoudre les inéquations suivantes :
1.
La fonction logarithme népérien est strictement croissante sur .
2.
( car ln 3 > 0)
Exercice 5 :
Déterminer les primitives des fonctions suivantes :
1. .
une primitive est de la forme .
2.
une primitive est de la forme .
Exercice 6 :
Soit pour x ∈ R.
1. Déterminez les limites de f aux bornes du domaine de définition.
et
2. Etudiez les variations de f.
sur
donc f est croissante sur
.
3. Construisez la courbe C représentant f.
Exercice 7 :
Résoudre les équations et inéquations proposées.
Calculons la valeur du discriminant :
Le discriminant est strictement positif, il existe donc deux racines réelles distinctes.
Exercice 8 :
1.a) Pour calculer la dérivée de , on utilise la formule pour la dérivée d’un quotient :
En simplifiant, on obtient :
b) Le dénominateur est toujours positif car x est dans l’intervalle [10, 100].
Le numérateur est positif pour x > 30 et négatif pour x < 30.
Donc, le signe de dépend du signe de (x-30)(x+30). On peut établir le tableau de signes suivant :
x | 10 | 30 | 100
—-|—–|—–|—–
| – | 0 | +
En utilisant ce tableau, on peut établir le tableau de variation de :
x | 10 | 30 | 100
—-|—–|—–|—–
| + | mín | +
c) Le coût unitaire est le plus bas lorsque est minimal.
Comme la fonction est décroissante sur [10,30] et croissante sur [30,100], son minimum est atteint en x = 30. Le coût unitaire minimal est donc
.
Le bénéfice de l’entreprise par objet vendu est la différence entre le prix de vente et le coût unitaire, soit :
2. Le bénéfice global de l’entreprise est donné par la formule , car l’entreprise fabrique et vend x objets par jour.
En remplaçant par son expression en fonction de x, on obtient :
3. Pour trouver le maximum de la fonction B sur [10,100], on peut calculer sa dérivée :
La dérivée est nulle en x = 55, ce qui est bien dans l’intervalle [10,100]. Pour déterminer que cette valeur est un maximum, on peut regarder le signe de la dérivée dans les intervalles [10,55] et [55,100]. On peut établir le tableau de signes suivant :
x | 10 | 55 | 100
—-|—–|—–|—–
B^'(x) | – | + | –
Donc, la fonction B est décroissante sur [10,55] et croissante sur [55,100], avec un maximum en x = 55. Le bénéfice maximal est donc .
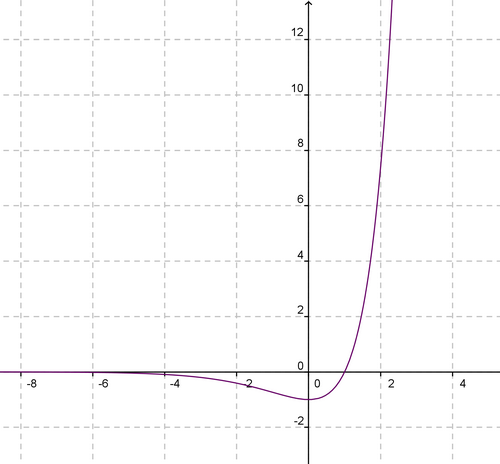
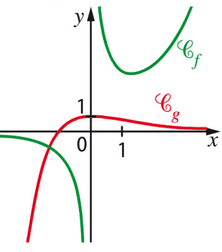
Exercice 9 :
La courbe représente une fonction f définie par .
Elle passe par les points de coordonnées (o;2) et (-2;0).
1) Calculer a et b .
Conclusion :
2) Déterminer les coordonnées du maximum après avoir étudié les variations de f.
f est dérivable sur en tant que produit de fonctions dérivables sur cet intervalle .
Le signe de f ‘ est celui de -x-1 puisque l’exponentielle est strictement positive sur R .
Conclusion : f est croissante sur .
Exercice 10 :
Simplifier au maximum :
Exercice 11 :
Exercice 12 :
Exercice 13 :
1. On peut remarquer que l’équation peut être mise sous la forme d’une équation du second degré en en posant
:
On peut résoudre cette équation en utilisant la méthode habituelle pour résoudre une équation quadratique :
Donc, ou
. En remplaçant par
, on trouve que les solutions de l’équation sont :
(pas de solution réelle) ou
2. On factorise par :
Donc, (pas de solution réelle) ou
3. On peut remarquer que l’équation est similaire à , qui est équivalente à
.
En utilisant la définition de la fonction cosinus hyperbolique inverse (aussi appelée arccosh), on a :
ou
donc les solutions de l’équation sont .
4. On peut diviser les deux membres de l’inéquation par pour obtenir :
En utilisant la même astuce que précédemment, on remarque que cette inéquation équivaut à .
Or, on sait que pour tout
, donc il n’y a pas de solution à cette inéquation.
5. On peut réécrire l’inéquation sous la forme , ce qui peut être factorisé en
.
On peut résoudre cette inéquation en utilisant le tableau de signes suivant :
|
|
|
— | — | — | —
| | |
| | |
Produit | | |
Donc, les solutions sont .
6. On peut appliquer la fonction exponentielle des deux côtés de l’inéquation, en prenant soin de conserver le sens de l’inégalité :
En utilisant la propriété de la fonction exponentielle , on peut appliquer le logarithme naturel des deux côtés de l’inégalité :
En multipliant par le dénominateur (qui est toujours positif puisque
), on obtient :
On peut résoudre cette inéquation en utilisant la méthode habituelle pour résoudre une inéquation quadratique :
ou
Mais on doit également vérifier que le dénominateur de la fraction initiale est toujours positif dans l’intervalle des solutions (c’est-à-dire ),
sinon nous aurions une solution qui ne fonctionne pas.
Le dénominateur est toujours positif dans cet intervalle, donc l’ensemble des solutions de l’inéquation initiale est
.
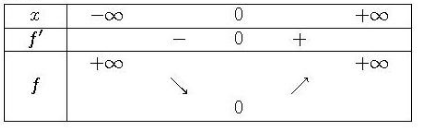
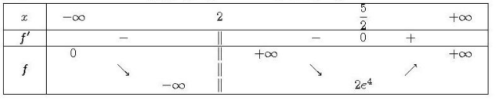
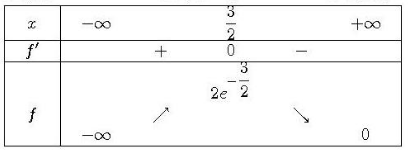
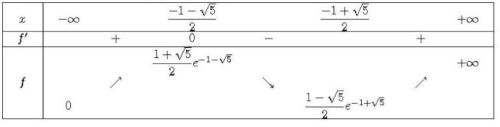
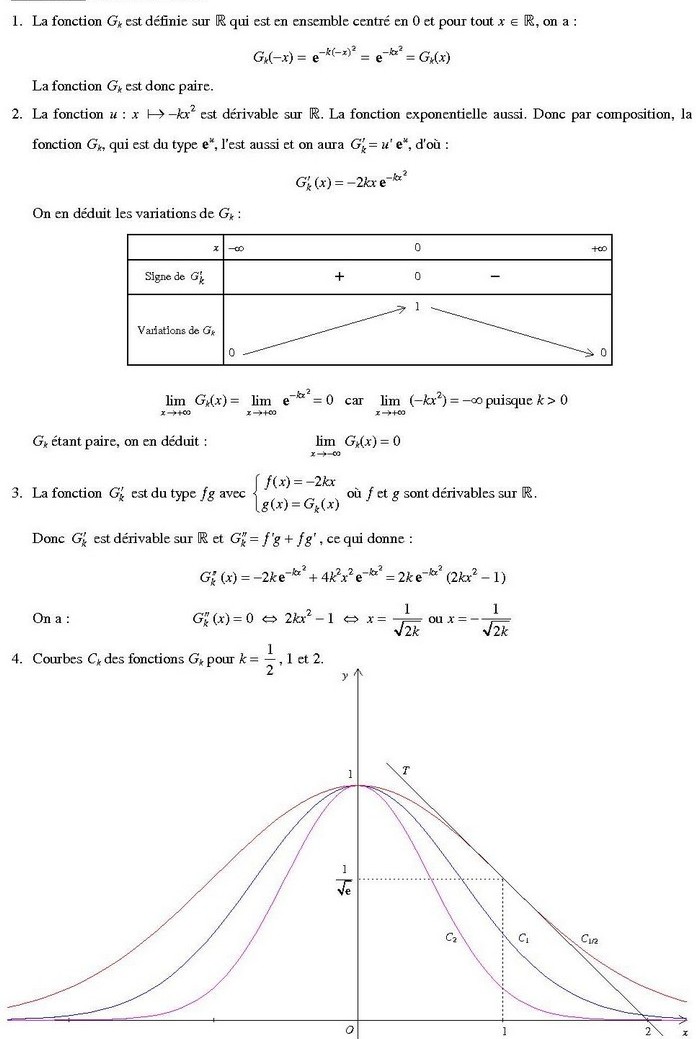
1. Pour tout , on a :
Donc, la fonction est paire.
2. La fonction est bien dérivable sur
car elle est la composée de fonctions dérivables. Pour tout
, on a :
En utilisant le signe de et le tableau de variations de
, on peut établir le tableau de variation de
:
x |-\infty | 0 |\infty
———|————–|——–|——
G_k(x) |+\infty reste | 1 |+\infty reste
G’_k(x) | – | 0 |+
3. Pour résoudre , on doit chercher les valeurs de
pour lesquelles
. Cette équation est vraie si et seulement si
ou
. La valeur
n’est pas une solution car ce point correspond à un maximum local de la fonction
. Donc, les solutions doivent vérifier
, c’est-à-dire
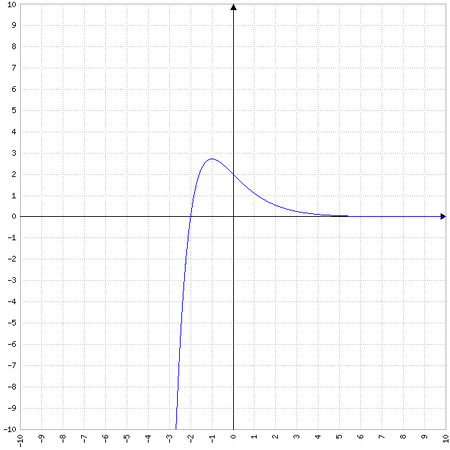
. Mais cette équation n’a pas de solution réelle car l’exponentielle est toujours strictement positive.
4. Voici les courbes de pour
:

5. Pour tout et pour tout
, on a :
Cela s’explique par le fait que le coefficient est plus petit (ou égal) que le coefficient
, donc l’exponentielle décroît moins rapidement pour
que pour
, ce qui fait que la fonction
est plus grande (ou égale) que la fonction
pour tout
.
6. L’équation équivaut à
, qui a pour solution positive
.
7. La tangente à la courbe de au point d’abscisse
est la droite affine de coefficient directeur
et passant par le point
. On a donc :
soit :
8. Voici le graphique de la fonction ainsi que de sa tangente en
:
Exercice 16 :
Partie A
1a. Soit une fonction définie et dérivable sur
telle que
pour tout
. En dérivant cette égalité par rapport à
, on a :
Pour que soit solution de l’équation différentielle
donnée, il faut que
pour tout
. En utilisant l’expression de
en fonction de
, on a :
Donc est solution de
si et seulement si
pour tout
.
1b. En intégrant par rapport à
, on obtient :
D’après la question précédente, la fonction correspondante est donnée par :
2a. Soit une fonction définie et dérivable sur
. Alors
est solution de
si et seulement si
est solution de l’équation différentielle
. En effet, en substituant
à
dans l’équation
, on obtient :
Pour que soit solution de
, il faut et il suffit que
pour tout
, c’est-à-dire que
pour tout
. On obtient ainsi que
est solution de
.
2b. L’équation est une équation différentielle linéaire d’ordre 1 à coefficients constants. Sa solution générale est donnée par
pour une constante
fixée en fonction des conditions initiales. Ici, on cherche à résoudre
avec la condition initiale
. En substituant
dans cette condition initiale, on obtient
, donc la solution de cette équation avec cette condition initiale est
.
2c. Pour tout entier , notons
la solution de
avec la condition initiale
. On peut écrire :
donc pour une certaine constante
. En utilisant la condition initiale
, on a
, donc :
Ainsi, pour tout , la solution de
avec la condition initiale
est donnée par :
2d. En particulier, la solution de avec la condition initiale
est donnée par
, donc d’après la question précédente, la solution de
avec la condition initiale
est donnée par
pour tout
.
Partie B
1a. On a :
et , donc
est solution de
.
Soit un entier strictement positif. Supposons que
est solution de
. Alors la solution
de
telle que
est donnée par la formule de la partie A :
En effet, la solution générale de est de la forme
pour une constante
, et la condition
donne
. On obtient ainsi que la solution
de
telle que
est donnée par :
Ce résultat est vrai pour tout entier , donc
est la solution de
avec la condition initiale
.
1b. Pour tout réel , on a
, donc par récurrence sur
et par la question 1a, on obtient :
En intégrant ces inégalités sur l’intervalle , on obtient :
On en déduit que pour tout entier
. En utilisant le théorème des croissances comparées, on obtient que
, donc la suite
converge vers 0.
1c. Pour tout réel , on a
, donc en intégrant ces inégalités sur l’intervalle
, on obtient :
D’après la question précédente, la suite converge vers 0. En utilisant la question 2b, on a :
Donc la série 
. D’après la question précédente, on a :
Ainsi, » 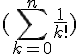
1d. Par définition, , donc la solution de
avec la condition initiale
est
. D’après la question 2c de la partie A, la solution de
avec la condition initiale
est
pour tout entier
.
Exercice 17 :
a. On a .
b. On a .
Exercice 18 :
On a , donc
.
On a , donc
.
En utilisant , on trouve que
.
Exercice 19 :
1.
a. .
b. .
c. .
2.
a. .
b. .
c. .
Exercice 20 :
1. On a , donc l’équation de
est
, ou
.
2. On cherche les valeurs de a pour lesquelles la droite passe par l’origine,
c’est-à-dire pour lesquelles ,
c’est-à-dire pour lesquelles a=1, puisque et que, pour
et
.
Donc il y a deux solutions : a=1 ou a=-2.
Exercice 21 :
1.
a. Avant la mise en marche, t=0, donc °C.
b. Après une journée de fonctionnement, , donc
°C.
2. On a, donc la température moyenne tend vers -10,5°C quand le temps tend vers l’infini.
Exercice 22 :
1.
a. .
b. .
c. .
d. .
e. .
f. .
g. .
h. .
i. .
j. .
k. .
l. .
m. .
n. .
o. .
p. .
Exercice 23 :
1.
a. On a .
b. On a .
c. .
d. .
e. .
f. .
g. .
h. .
i. .
j. .
k. .
l. .
Exercice 24 :
1.
a. On a .
b. On a .
c. On a .
2.
a. On a pour
, donc f est décroissante sur
.
b. On a pour
, donc f est décroissante sur
.
c. On a pour tout x, donc f est croissante sur
.
Exercice 25 :
1. On a , donc la limite de f en
est 0.
2. On a , qui est strictement négative sur
, donc f est décroissante sur cet intervalle.
3. La conjecture est que la fonction f est décroissante sur , ce qui est effectivement vrai d’après 2.
En effet, la dérivée est strictement négative sur tout l’intervalle de définition de f, donc f est décroissante sur cet intervalle.
Exercice 26 :
1. On a .
2. On a pour tout
, donc f est décroissante sur cet intervalle.
3. On sait que f est décroissante sur , donc son maximum est atteint en x=0 et son minimum en
.
On peut calculer f(0)=2 et.
On a également (car
tends vers 0 plus vite que x tend vers -∞) et f est décroissante sur
.
Donc le tableau de variation de f est :
x | | 0 |
f'(x) | + | 0 | –
f(x) | | 2 |
Exercice 27 :
1.
a. On a .
b. On a .
c. On a 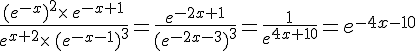
Exercice 28 :
1.
On a .
2.
On a .
3.
On a .
Exercice 29 :
1) En posant , on peut réécrire l’équation
sous la forme
.
Cette dernière équation correspond à une équation du second degré se factorisant en .
Donc, on a ou
, c’est-à-dire
ou
.
Or, est toujours strictement positif, donc on ne peut pas avoir
.
Ainsi, l’équation est équivalente à l’équation
.
2) On vient de montrer que est équivalente à
.
On peut donc résoudre l’équation .
En posant , on a
, qui correspond à une équation du second degré se factorisant en
.
Ainsi, on a ou y+2=0, c’est-à-dire
ou
.
Or, e^x ne peut pas être négatif, donc on ne peut pas avoir .
D’où la solution de l’équation est
.
Exercice 30 :
1) On peut réécrire l’inéquation sous la forme
, c’est-à-dire
. Ainsi, on a deux cas à étudier :
– Si , alors l’inéquation équivaut à
, c’est-à-dire
, d’où x<0.
– Si , alors l’inéquation équivaut à
, c’est-à-dire
, d’où
.
Finalement, la solution de l’inéquation est x<0.
2) On peut réécrire sous la forme
.
On vient de montrer que pour tout
, donc le numérateur est négatif dans cette intervalle.
De plus, le dénominateur est toujours positif.
Ainsi, est négatif sur
.
Exercice 31 :
Conjecture : On a et
.
Démonstration :
– Pour la limite en 0, on peut utiliser le développement limité de au premier ordre au voisinage de 0 :
.
Ainsi, on a , d’où
.
– Pour la limite en , on a
, qui tend vers 0 quand x tend vers
.
– Pour la limite en , on peut réécrire
sous la forme
, qui tend vers 0 quand x tend vers
.
En effet, on a et
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonction exponentielle : corrigé des exercices de maths en terminale en PDF.» au format PDF.
Ressources de première
Cours de première
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.