Dérivée d’une fonction : exercices de maths en 1ère corrigés en PDF.

Mis à jour le 29 mai 2025

Sommaire

✏️Exercices

1ère • Lycée

Dérivée d’une fonction

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

La dérivée d’une fonction et l’interprétation graphique du nombre dérivée à travers des exercices de maths en 1ère corrigés. L’élève devra être capable d’étudier l’a taux d’accroissement d’une fonction en un point et déterminer le nombre dérivé. Connaître toutes les formulés de dérivation afin d’étudier le sens de variation de la fonction et de tracer sa courbe. Savoir déterminer l’équation de la tangente en un point de la courbe représentative en première.

Exercice 1 :

Dériver la fonction f dans les cas suivants :

2. $f(x)=\frac{3x^2-4x+2}{2} .$

3. $f(x)=(\sqrt{x+1})\times (x^2-2) .$

4. $f(x)=(2x-\sqrt{x})\times (x+4) .$

5. $f(x)=\frac{1}{1-4x} .$

6. $f(x)=\frac{-3}{2x-1} .$

7. $f(x)=\frac{2x-1}{3x+2} .$

8. $f(x)=\frac{3x^2-4x+1}{2x-3} .$

10.

11. $f(x)=\sqrt{3x-4}.$

12. $f(x)=2x\sqrt{-3x+2}.$

Exercice 2 :

Déterminer une équation de la tangente T à la courbe représentative de la fonction f au point d’abscisse a dans les cas suivants :

1. f(x)= 3x²-x+1 avec a= -1.

2. $f(x)=\frac{2x-1}{x-2}$ avec a= 3.

3. $f(x)=\frac{\sqrt{x}}{x}$ avec a= 9.

Exercice 3 :

Soit f la fonction définie sur $\mathbb{R^*}$ par :

$f(x)=\frac{-x^2+2x-1}{x}$ .

On note C sa courbe représentative dans un repère orthonormé .
1. Déterminer les abscisses des points de la courbe C où la tangente est horizontale .
2. Existe-t-il des points de la courbe C où la tangente admet un coefficient directeur égal à – 2 ?

3 Déterminer les abscisses des points de la courbe C où la tangente est parallèle à la droite d’équation $y=- \frac{2}{3}x-5$ .

Exercice 4 – Equation de la tangente à une courbe représentative

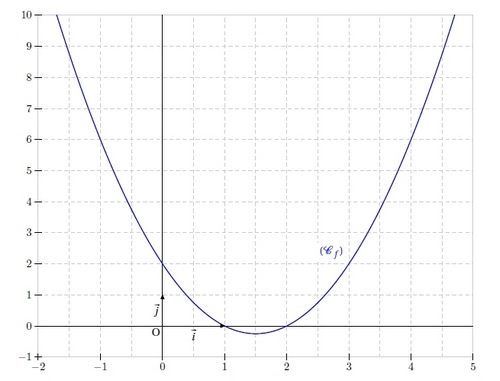
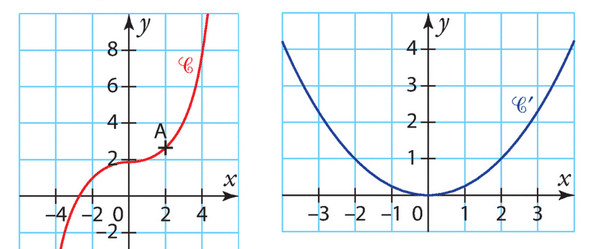
Soit f la fonction définie sur R par .
Soit (Cf ) sa courbe représentative.

1. Donner, en justifiant, l’équation de la tangente (T) à la courbe (Cf ) au point A d’abscisse 0.

2. Tracer dans un même repère la courbe (Cf ) et la tangente (T) sur l’intervalle [- 1 ; 1,5].

Exercice 5 – Calculer une limite

Le but de cet exercice est de calculer la limite suivante :

$\lim_{h \to 0}\frac{(1+h)^{2005}-1}{h}$ .

Pour cela on considère la fonction définie sur $\mathbb{R}$ par $f(x)=(1+x)^{2005}$ .

1. Calculer la dérivée f’ de la fonction f. Calculer f ‘ (0).

2. Calculer l’accroissement moyen de la fonction f entre 0 et h. En déduire la limite ci-dessus.

Exercice 6 – Prix de revient et vitesse d’un camion

Un camion doit faire un trajet de 150 km.
Sa consommation de gasoil est de $6+\frac{v^2}{300}$ litres par heure, où désigne sa vitesse en km/h .
Le prix du gasoil est de 0,9 € le litre et on paie le chauffeur 12 € par heure.

1. Soit t la durée du trajet en heure. Exprimer t en fonction de la vitesse .

2. Calculer le prix de revient P(v) du trajet en fonction de v.

3. Quel doit être la vitesse v du camion pour que le prix de revient P(v) de la course soit minimal ?

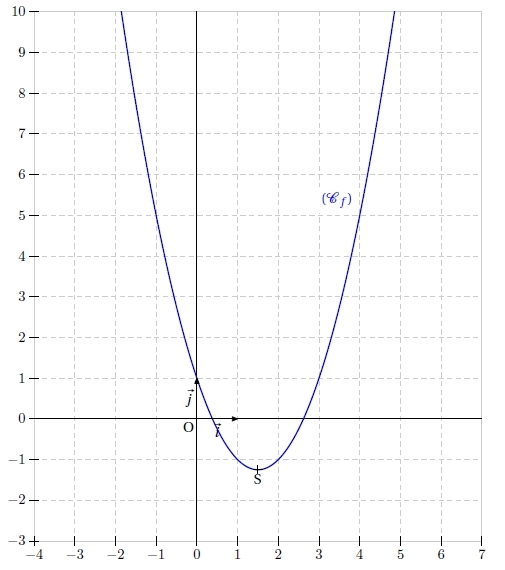
Exercice 7 – Sommet d’une parabole

Soit (P) la parabole définie par la fonction .
Calculer les coordonnées de son sommet S.

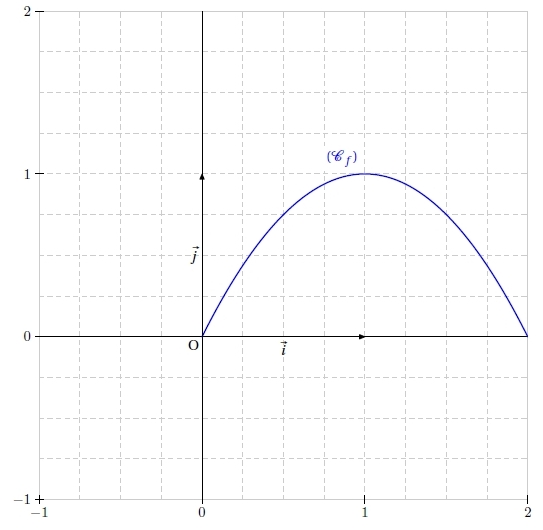
Exercice 8 – Etude d’un rectangle

On considère un rectangle dont le périmètre P est égal à 4 cm.

1. Déterminer ses dimensions (longueur L et largeur l) sachant que son aire S est égale à $\frac{3}{4}$ cm².

2. On recherche maintenant les dimensions du rectangle de façon que son aire S soit maximale.

a. Exprimer S en fonction de la largeur l.

b. On considère la fonction f définie sur $\mathbb{R}$ par .

Calculer la dérivée f’ de f puis étudier son signe.

Dresser le tableau de variations de la fonction f.

Tracer la représentation graphique (Cf ) de la fonction f sur [0 ; 2].

c. En déduire les dimensions du rectangle dont le périmètre P est égal à 4 m et l’aire S est maximale.

Exercice 9 – Fonction numérique et racine

On considère la fonction f définie sur R par : .
On note (Cf ) sa représentation graphique.

1.Calculer la dérivée f ‘ de f puis étudier son signe.

2. Dresser le tableau de variations de la fonction f.

3. Déterminer une équation de la tangente (T) à (Cf ) au point d’abscisse 0.

4. Tracer (T) et (Cf ) dans un même repère.

5. Démontrer que l’équation f(x) = 0 admet une solution unique $\alpha$ dans l’intervalle [2 ; 3].

6. Donner une valeur approchée de $\alpha$ , par défaut, à $10^{-1}$ près.

Exercice 10 – Tableau de variation et équation

1. Dresser le tableau de variations de la fonction f définie sur R par :
2. Résoudre l’équation f(x) = 0.

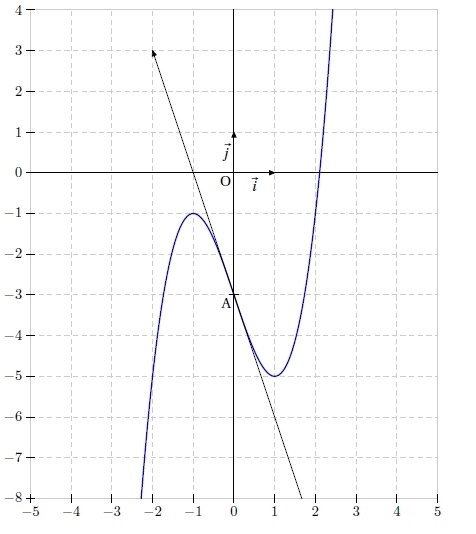
Exercice 11 – Etude de deux fonctions et des tangentes

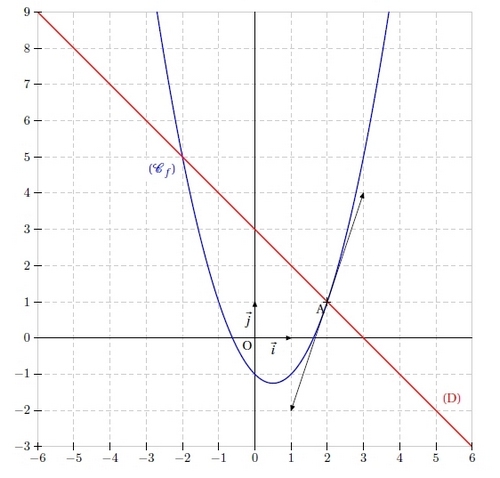
On considère la fonction définie par .
On note (Cf ) sa courbe représentative.
On considère également la fonction g définie par g(x) = 3 – x.
On note (D) sa représentation graphique.

1. Calculer la dérivée f’ de f.

2. Déterminer une équation de la tangente (T) à la courbe (Cf ) au point d’abscisse x_0=2 .

3. Résoudre par le calcul l’équation g(x) = f(x).

4. Préciser les coordonnées des points d’intersections de (Cf ) et (D).

5. Tracer sur un même repère les droites (T), (D) et la courbe (Cf ).

Exercice 12 – Déterminer la dérivée de fonctions numériques

Dériver les fonctions suivantes :

$f(x)=4x^2-3x+1\\g(x)=(2x+3)(3x-7)\\h(x)=\frac{2x+4}{3x-1}\,pour\,x\neq\frac{1}{3}\\k(x)=(2x^2+3x+1)^2$

Exercice 13 – Dérivée de plusieurs fonctions

Dériver les fonctions suivantes :

$f(x)=x^2\\g(x)=3x^4-2x^3+5x-4\\h(x)=\sqrt{x}(1-\frac{1}{x})\\k(x)=\frac{x+5}{x^2+1}$

Exercice 14 – Valeur absolue et dérivabilité

Soit une fonction définie sur $\mathbb{R}$ par .

Etudier la dérivabilité de sur $\mathbb{R}$ .

Exercice 15 – Dérivée d’une fonction puissance

Démontrez que si u est une fonction dérivable sur un intervalle I, alors:

a) u² est dérivable sur I et (u²)’=2uu’.

b) u³ est dérivable sur I et (u³)’=3u²u’.

Exercice 16 – Sens de variation

On considère la fonction f définie par sur $\mathbb{R}$ .

1. Démontrer que $f(x)\leq\,,\frac{1}{4}$ pour tout x appartenant à $\mathbb{R}$ .

2. En déduire que la fonction f admet un maximum en $x=\frac{1}{2}$ .

3. Démontrer que $f(x)=\frac{1}{4}-,(,x-\frac{1}{2},,)^2$ .

4. En déduire que la fonction f est croissante sur l’intervalle $]-\infty;\frac{1}{2}[$ et décroissante sur $]\frac{1}{2};+\infty[$ .

Exercice 17

Soit la fonction définie sur $\mathbb{R}$ par

1. Etudier les variations de sur $\mathbb{R}$ .

2. Déterminer les coordonnées des points d’intersection entre la courbe représentative de et la droite d’équation $y=\frac{1}{2}x-2$ .

Exercice 18

Etudier les variations sur $\mathbb{R}$ de la fonction f définie par .

Exercice 19

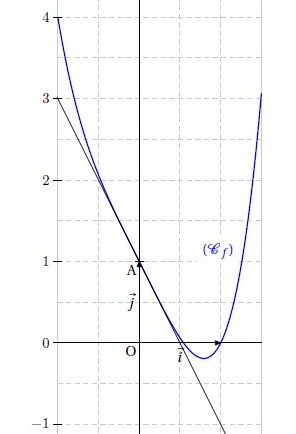
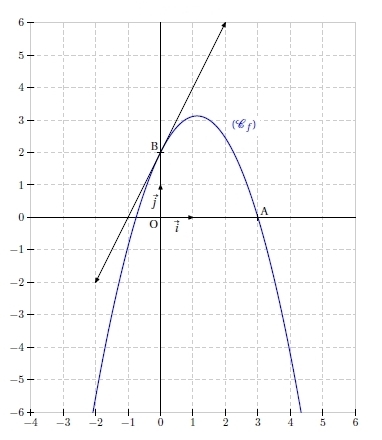
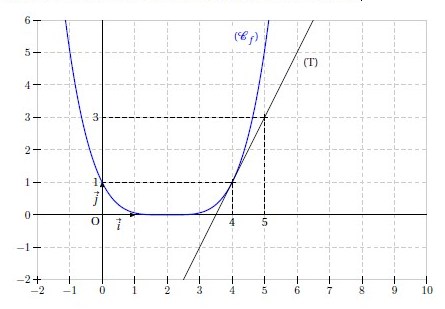
Soit f la fonction définie sur $\mathbb{R}$ par :

$f(x)=\frac{-4x-4}{x^2+2x+5}$ .

1. Etudier les variations de f sur $\mathbb{R}$ .

2. Déterminer les coordonnées du point A, intersection entre la courbe représentative de f et l’axe des abscisses .

3. Déterminer une équation de la tangente T à la courbe représentative de au point A.

Exercice 20

Etudier les variations sur ]-2 ; 1[ de la fonction définie par :

$f(x)=\frac{-5x^2+4x-8}{x^2+x-2}$ .

Exercice 21 – Courbe représentative, dérivée et tangente

Soit la fonction définie sur $\mathbb{R}$ par $f(x) = \frac{1}{4}x^4 -2x^2 + 3$

On appelle C_f sa représentation graphique dans un repère orthonormal.

1) a) Etudier la parité de . Que peut-on en déduire pour C_f ?

b) Déterminer l’expression de la fonction dérivée de et en déduire le tableau de variation de

2) a) Déterminer une équation de la tangente à C_f au point d’abscisse 1.

b) Cette tangente recoupe C_f en deux autres points.

b.1) Montrez que les abscisses de ces points sont les solutions de l’équation :

b.2) Vérifiez que l’on a :

b.3) En déduire les abscisses de ces points.

Exercice 22 – Parabole et tangentes

Soit (P) la parabole d’équation $y=x^2-3x+\frac{5}{4}$

et (H) l’hyperbole d’équation $y=\frac{3(3x+5)}{4(x+3)}$ .

Le plan est ramené à un repère orthonormal.

1) Montrer que (P) et (H) rencontrent l’axe (Oy) en un même point A.

2) Montrer que les tangentes en A aux courbes (P) et (H) sont perpendiculaires.

Rappel : Dans un r.o.n deux droites sont perpendiculaires si et seulement si le produit de leur coefficient directeur est égal à –1 .

Exercice 23 – Tangente et déterminer un réel

Déterminer le réel m pour que la courbe d’équation

admette au point d’abscisse –1 une tangente de coefficient directeur 6.

Exercice 24 – Déterminer l’abscisse d’une tangente

Soit la fonction $f:x \mapsto \frac{-x^2 +2x-1}{x}$ définie sur $\mathbb{R}^*$ et soit (C) sa courbe représentative.

Déterminer les abscisses des points de (C) où la tangente :

1) est horizontale

2) est parallèle à la droite d’équation $y=-\frac{2}{3}x-5$ .

Exercice 25 – Retrouver l’expression d’une fonction carrée

Une parabole (P) admet dans un repère $(O;\vec{i},\vec{j})$ une équation du type :

$y=ax^2+bx+c\,(a\neq0)$
1. Déterminer les coefficients a, b et c sachant que (P) coupe l’axe des abscisses au point A d’abscisse 3, l’axe des ordonnées au point B d’ordonnée 2 et qu’elle admet en ce point la droite d’équation y = 2x + 2 pour tangente.

2. Indiquer l’abscisse du second point d’intersection de (P) avec (Ox).

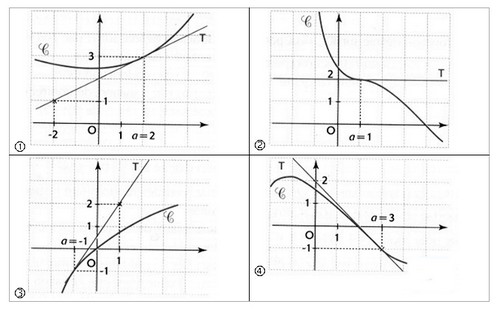
Exercice 26 – Nombre dérivée et tangente à une courbe

Dans chaque cas détermine f'(a) et donner une équation de la tangente T.

Exercice 27 – Equation de tangente à une parabole
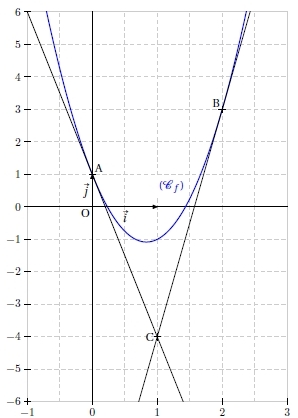
On considère la fonction f définie par :

dont la parabole (Cf ) passe par les points A (0 ; 1) et B (2 ; 3).

Les tangentes en A et B se coupent au point C (1 ; – 4).

1. Déterminer une équation des tangentes à (Cf ).

En déduire f ‘ (0) et f ‘ (2).

2. Exprimer f ‘ (x) en fonction de a, b et c.

3. A l’aide des valeurs de f ‘ (0), f ‘ (2) et f(0), trouver trois équations vérifiées par a, b et c puis déterminer l’expression algébrique de la fonction f.

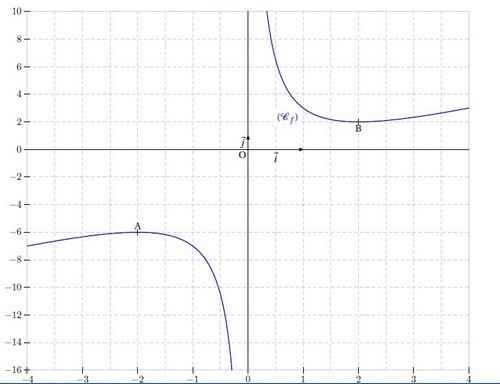
Exercice 28 – Limite en l’infini et tableau de variation
On considère la fonction définie sur $\mathbb{R}$ par $f(x)=\frac{x}{x^2+1}$ .

1. Calculer les limites de f en $+\infty$ et en $-\infty$ .

2. Calculer la dérivée f » de f et étudier son signe.

3. Dresser le tableau de variation de la fonction f.

Exercice 29 – Lecture graphique
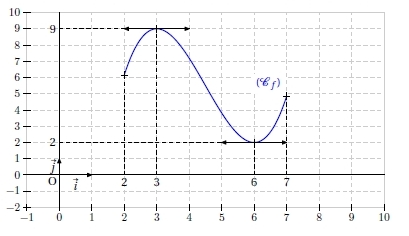
Ci-dessous est donnée la courbe (Cf ) représentant une fonction f définie et dérivable sur l’intervalle [2 ; 7].

1. Par lecture graphique, donner sans justifier la valeur de :

f(3) ; f ‘ (3) ; f(6) ; f ‘ (6).

2. Le graphique ne permet pas la lecture de f ‘ (4).
Préciser néanmoins son signe. Expliquer.

Exercice 30 – Calcul d’une dérivée et tableau de variation
Soit la fonction définie sur $\mathbb{R}$ par .

1. Calculer la dérivée et étudier son signe.

2. Dresser le tableau de variations de la fonction f.

Exercice 31 – Lecture graphique du nombre dérivé

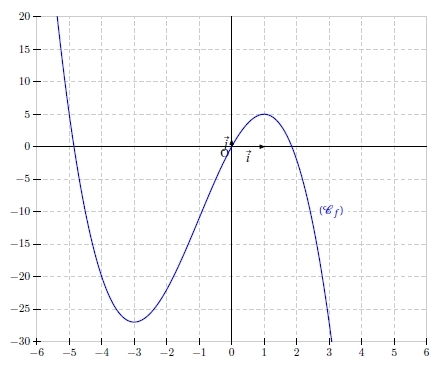
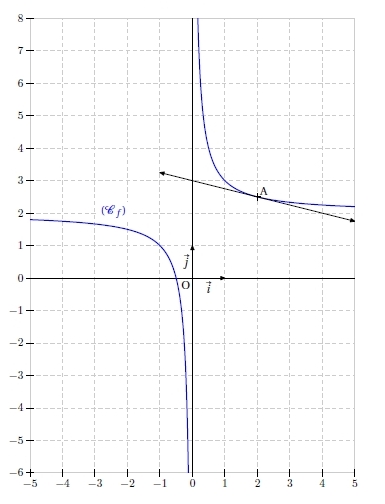
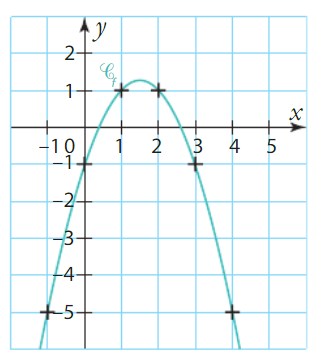
Sur le graphique ci-dessous sont représentées la courbe (Cf ) de la fonction f définie sur $\mathbb{R}$ par :

$f(x)=(1-\frac{x}{2})^4$ ainsi que la tangente (T) à (Cf ) au point d’abscisse x_0=4 .

1. Donner, par lecture graphique, et sans justifications, la valeur du nombre f ‘ (4).

2. Déterminer, à l’aide du calcul de la dérivée de f, la valeur du nombre f ‘ (3).

Exercice 32 – Dérivabilité en un point

Soit la fonction définie sur $\mathbb{R}^*$ par $f(x)=\frac{1}{x}+2$ .

1. Montrer que f est dérivable en 2.

2. Déterminer une équation de la tangente (T) à la courbe (Cf ) représentant f au point d’abscisse 2.

Exercice 33 – Calcul de dérivée et du nombre dérivé

1. Dériver les fonctions f et g définies ci-dessous :

$f(x)=\frac{x}{x+\sqrt{x}}\,sur\,]0;+\infty[$

$g(x)=(\frac{1}{1+x})^3\,sur\,\mathbb{R}-\{-1}$

2. Calculer f ‘ (16) et g ‘ (2).

Exercice 34 – Sens de variation et encadrement
1. Etudier le sens de variation de la fonction définie sur $\mathbb{R}$ par :.

2. En déduire un encadrement de f(x) sur [0 ; 2].

Exercice 35 – Etude d’une fonction numérique
On considère la fonction définie sur $\mathbb{R}^*$ par $f(x)=x-2+\frac{4}{x}$ .

1. Calculer la dérivée f ‘ et étudier son signe.

2. Dresser le tableau de variations de la fonction f.

3. Tracer la représentation graphique (Cf ) de la fonction f sur $[-4 ; 0[\cup ]0 ; 4]$ .

Exercice 36 :

Déterminer sur quel ensemble est dérivable chacune des fonctions suivantes, puis déterminer sa dérivée.

a) $f:\,x\,\mapsto \,5x^2-\,3x+\,2$ définie sur $\mathbb{R}$ .

b) $g:x\,\mapsto \,100+\frac{1}{x}$ définie sur $\mathbb{R}^*$ .
c) $h:x\,\mapsto \,x\sqrt{x}$ définie sur $[0;+\infty[$ .

d) $j:x\,\mapsto \,\frac{12-5x}{9x+2}$ définie sur $\mathbb{R} - \{-\frac{2}{9} \}$ .

Exercice 37 :

Soit g la fonction définie sur $\mathbb{R}$ par $g:x\mapsto (-9x+ 1)^5$ .

Déterminer sur quel ensemble elle est dérivable puis déterminer sa dérivée.
Exercice 38 :

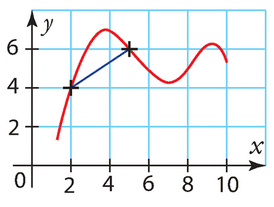
La fonction f est représentée par la courbe rouge ci-dessous.

Quel est le taux de variation de f entre 2 et 5 ?

Exercice 39 :

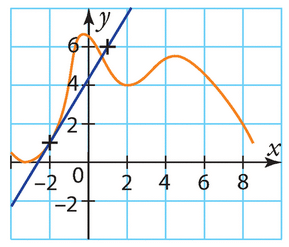
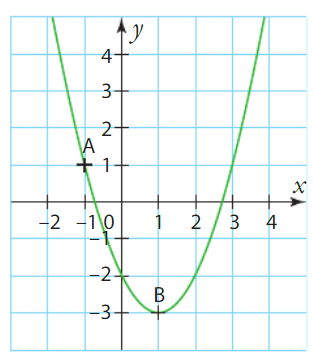
Sur le graphique ci-dessous la tangente en A(-2; 1) à la courbe

représentative d’une fonction f définie sur [-4 ; 9] passe par le point B(1 ; 6).
Déterminer f ‘ (-2).

Exercice 40 :

Soit f la fonction définie sur $[0;+\infty[$ par $f:x\,\mapsto \,\sqrt{x}-3$
et h un nombre réel non nul.
1. Montrer, à l’aide de l’identité remarquable
(a – b)(a + b) = a² – b², que le taux de variation de f entre 9 et 9 + h est égal à
$\frac{1}{\sqrt{9+h}+3}$ .

2. En déduire que la fonction est dérivable en 9 et déterminer f ‘ (9).
Exercice 41 :

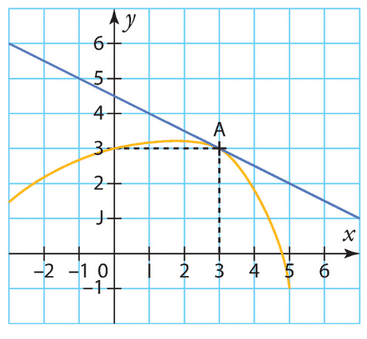
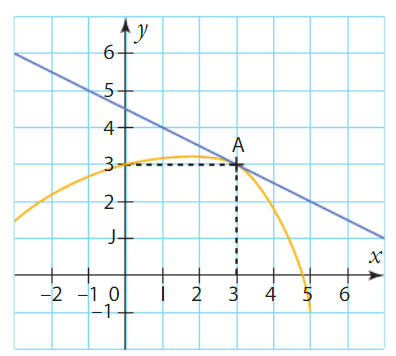
La courbe d’une fonction g définie sur [-3 ; 5] est représentée ci-dessous.

La tangente à cette courbe au point A d’abscisse 3 passe par le point de coordonnées (-3 ; 6).
Que vaut g(3) ? Que vaut g ‘ (3) ?

Exercice 42 :

Chacune des fonctions suivantes est de la forme d’une somme de deux fonctions u + v.

Dans chaque cas, identifier les fonctions u et v, et donner leurs ensembles de dérivabilité.

En déduire sur quel ensemble la fonction « somme » est dérivable,

puis déterminer l’expression de sa fonction dérivée.

$f:x\,\mapsto \,\frac{1}{x}+x$ $g:x\,\mapsto \,-5+\frac{1}{x^2}$ $h:x\,\mapsto \,x^4+x^2$

Exercice 43 :

Utiliser Geogebra pour répondre aux questions suivantes

portant sur la fonction $f:x\,\mapsto \,\frac{-9}{2x^2-4x+3}$ .

1. Saisir l’équation de la courbe représentative de f:
«y=-9/(22-4x+ 3)».

2. Placer un point sur la courbe.

3. Tracer la tangente à la courbe en ce point.

4. Afficher le coefficient directeur de la tangente.

5. En sélectionnant le point et en le plaçant à la bonne abscisse,

déterminer une valeur approchée de f ‘ (-2) ; f ‘ (-1); f ‘(0) ; f ‘ (1) et f ‘(2).

Exercice 44 :

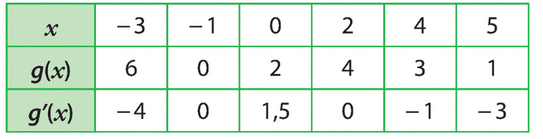
Soit g une fonction dérivable sur R. On a le tableau de valeurs suivant.

1. Dans un repère orthonormé placer les points de coordonnées (x; g(x)).

2. Construire en chacun de ces points les tangentes à la courbe C_g représentative de la fonction g.

3. Représenter une allure possible de C_g .
Exercice 45 :

On a représenté la courbe d’une fonction f en rouge et la courbe de sa fonction dérivée f ‘ en bleue.
Déterminer une valeur approchée du coefficient directeur de la tangente à 6 au point A d’abscisse 2.

Exercice 46 :

Déterminer pour chacune des fonctions suivantes, l’ensemble I sur lequel elle est dérivable,

puis sa fonction dérivée sur I.

$a)f(x)=\frac{5}{2x}+\frac{3}{4}-\frac{7x^2}{4}$ $b)g(x)=\frac{-4}{5x}(x-11)$

$c)h(x)=\frac{5x^2-8x+1}{21-7x}$ $d)j(x)=\frac{-5}{3x^2+2}$

$e)k(x)=\frac{9x}{x^2-6x+5}$ $f)m(x)=\sqrt{10-x}$

Exercice 47 :

La courbe représentative d’une fonction f définie sur R passe par les points A et B.

Quel est le taux de variation de f entre —1 et 1 ?

Soit fla fonction définie sur $\mathbb{R}$ par $f:\,x\,\mapsto \,11x-\,7$ et h un nombre réel non nul.
Déterminer le taux de variation de f entre 3 et 3 + h.

Exercice 48 :

Soit f une fonction définie sur $\mathbb{R}$ et h un nombre réel non nul.
On sait que $\frac{f(-7+h)-f(-7)}{h}=\frac{5}{3}(4h+9)$ .
Peut-on dire que la fonction f est dérivable en -7 ? Si oui, déterminer $f'(-\,7).$

Exercice 49 :

Soit g une fonction définie sur $\mathbb{R}$ et x un nombre réel proche de 3 mais différent de 3.

On sait que $\frac{g(x)\,-\,g(3)}{x-3}=2x+3$ .
Peut-on dire que la fonction g est dérivable en 3 ? Si oui, déterminer g'(3).

Exercice 50 :

La courbe d’une fonction g définie sur [- 3 ; 5] est représentée ci-dessous.
La tangente à cette courbe au point A d’abscisse 3 passe par le point de coordonnées (- 3 ; 6).
Que vaut g(3) ? Que vaut g'(3) ?

Exercice 51 :

Soit f une fonction dérivable sur $\mathbb{R}$ telle que $f'(2)\,=-1$ et $f\,'(0)\,=\,2$ .

Soit C_f sa courbe représentative dans le repère ci-dessous.
Reproduire la courbe C_f (en plaçant quelques points importants et en respectant l’allure) et tracer la tangente à C_f au point d’abscisse 2 et la tangente à C_f au point d’abscisse 0.

Exercice 52 :

Pour chacune des fonctions suivantes, dire sur quel ensemble elle est dérivable, puis déterminer l’expression de sa fonction dérivée.
$f:x\,\mapsto \,x^4;\,g:x\,\mapsto \,x^{12};h:x\,\mapsto \,x^{-1};$

Chacune des fonctions suivantes est de la forme d’une somme de deux fonctions u + v.

Dans chaque cas, identifier les fonctions u et v, et donner leurs ensembles de dérivabilité.

En déduire sur quel ensemble la fonction « somme» est dérivable, puis déterminer l’expression de sa fonction dérivée.

$f:x\,\mapsto \,\frac{1}{x}+x\,;\,g:x\,\mapsto \,-5+\frac{1}{x^2};h:x\,\mapsto \,x^4+x^2;$

Exercice 53 :

Chacune des fonctions suivantes est de la forme d’un produit de deux fonctions $u\,\times \,v$ .

Dans chaque cas, identifier les fonctions u et v, et donner leurs ensembles de dérivabilité.
En déduire sur quel ensemble la fonction « produit » est dérivable, puis déterminer l’expression de sa fonction dérivée.

$f:x\,\mapsto \frac{1}{x}(9-6x);\,g:x\,\mapsto \,x^2\sqrt{x};h:x\,\mapsto \,(x^5+x^3)(x^2-4);$

Exercice 54 :

Soit f la fonction définie sur $I=]-4;+\infty[$ par $f:x\,\mapsto \,\frac{1}{2x+8}$ .

1.f est de la forme $\frac{1}{v}$ .
Donner l’expression de la fonction v et résoudre l’équation v(x)=0.

2. En utilisant le théorème de la dérivée de l’inverse d’une fonction, démontrer que la fonction f est dérivable sur I et donner l’expression de sa dérivée .

Exercice 55 :

Soit h la fonction définie sur $I=]-4;+\infty[$ par $h:x\,\mapsto \,\sqrt{-3x+12}$ .
1. h est une fonction composée de deux fonctions g et f dans cet ordre.
Donner l’expression des fonctions g et f.
2. En utilisant le théorème de la dérivée d’une fonction composée, démontrer que la fonction h est dérivable sur l.
3. Déterminer l’expression de f'(x) pour tout réel strictement positif x et celle de g'(x) pour tout réel x de I.
4. En déduire l’expression de la dérivée .

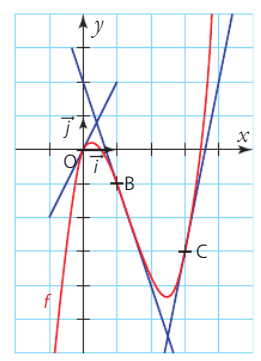
Exercice 56 :

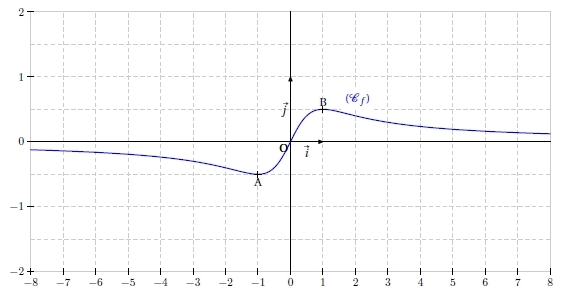
Dans le repère orthonormé (O ; i, J) ci-dessous, la courbe rouge C_f représente une
fonction f définie et dérivable sur $\mathbb{R}$ , les droites tracées en bleu représentent les
tangentes à C_f respectivement au point O, au point B d’abscisse 1 et au point C d’abscisse
3.

1. Déterminer graphiquement f'(0) , f'(l) et $f\,'(3).$
2. Déterminer l’équation réduite de la tangente à C_f au point C.
3. La courbe C_f est la représentation graphique de la fonction $f:\,x\,\mapsto \,x^3-4x^2\,+2x$ .
Retrouver par le calcul les résultats des questions 1. et 2.

5/5 - (20572 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «dérivée d’une fonction : exercices de maths en 1ère corrigés en PDF.» au format PDF.