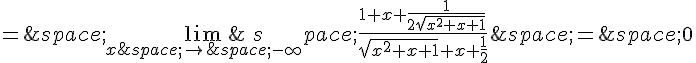Dérivée d’une fonction : corrigé des exercices de maths en terminale en PDF.
Mis à jour le 17 septembre 2025
Exercice 1 :
Etudier la fonction f définie sur
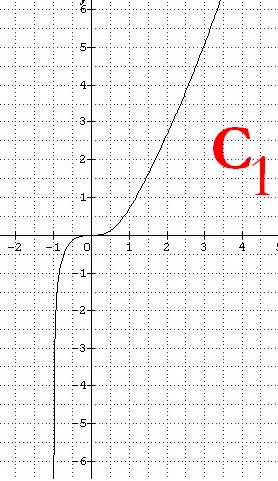
a.
f est une fonction polynomiale donc dérivable sur
Donc f est croissante sur
b.
f est une fonction rationnelle dérivable sur
f ‘ est négative sur D donc f est décroissante sur
c.
f est une fonction inverse dérivable sur
f ‘ est positive sur D donc f est croissante sur
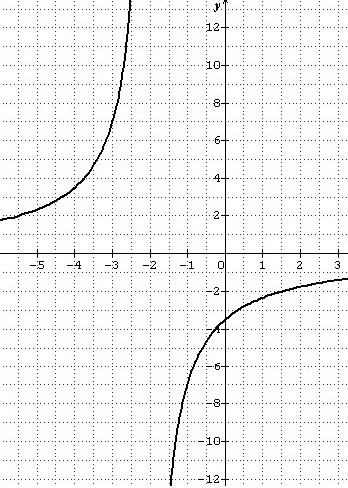
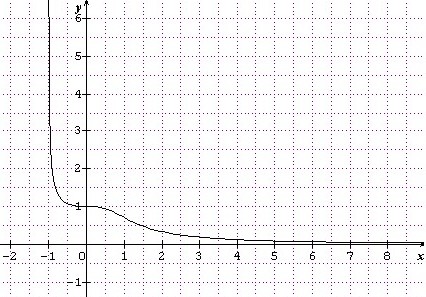
d.
f est une fonction racine carrée , définie et dérivable sur
f ‘ est négative sur D donc f est décroissante sur
e.
f ‘ est positive donc f est croissante sur
Exercice 2 :
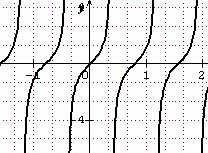
La fonction est dérivable sur
, strictement croissante sur ]
; -1] et sur [0 ;
[ et strictement décroissante sur [-1;0].
De plus,
Déterminer le nombre de solutions de l’équation
En utilisant la continuité de f sur et le théorème des valeurs intermédiaires (T.V.I), montrer que l’équation f(x)=1 admet deux solutions sur
Exercice 3 :
Etudier la fonction f définie sur .
a.
c’est une fonction polynomiale donc dérivable sur
donc f est croissante sur
b.
f est une fonction rationnelle dérivable sur
f ‘ est du signe du numérateur
f ‘ est donc négative et f décroissante sur
Exercice 4 :
Pour chacune des fonctions f suivantes :
• Indiquer l’ensemble de dérivabilité de la fonction .
• ,Calculer sa dérivée .
a. .
f est dérivable sur
b. .
f est dérivable sur
c. .
f est dérivable sur
d. .
f est dérivable sur
e. .
f est dérivable sur
f. .
f est dérivable sur
g. .
f est dérivable sur
h. .
f est dérivable sur
Exercice 5 :
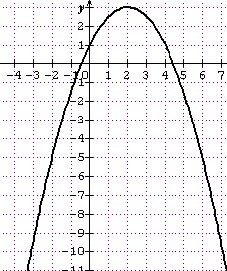
1. Déterminer les limites de aux bornes de son ensemble de définition.
Etudier le sens de variation de et construire
dans le repère
.
Soit
f ‘ est négative et f est donc croissante sur
2. Soit n un entier naturel non nul.
a. désignant la fonction dérivée de
, montrer que :
A montrer par récurrence…..
b. Etudier le sens de variation des fonctions et
puis dresser leur tableau de variation .
c. Tracer et
dans le repère
.
Exercice 6 :
1. Continuité de f en 0:
On doit démontrer que .
On a f(0) = 0 par définition de f(0).
Pour montrer que , on peut utiliser les deux inégalités suivantes:
pour tout x≠0, car |sin(1/x)| ≤ 1.
Pour tout ε>0, il existe tel que
implique
, en utilisant la majoration de
par 1 et le fait que x^2 → 0 lorsque x → 0.
Ainsi, on a:
Donc, , ce qui montre que f est continue en 0.
2. Dérivabilité de f en 0:
On doit déterminer si la limite existe.
On a f(0) = 0 par définition de f(0), et pour x≠0 on a:
.
Le facteur x sin(1/x) est borné (par -1 et 1), donc il tend vers 0 lorsque x tend vers 0. Ainsi, la limite f ‘(0) existe et vaut 0.
3. Non-continuité de f ‘ en 0:
On doit démontrer que la limite n’existe pas.
On peut calculer la dérivée f ‘(x) de f en x≠0 en utilisant la formule de dérivation d’un produit:
.
On remarque que pour tout entier n>0, on a et
, donc f ‘(x) prend des valeurs positives et négatives arbitrairement grandes près de 0.
En effet, pour tout M>0, on peut trouver un entier n>0 tel que 1/(nπ) < δ, où δ = min{1/(2Mπ), π/2}, et on a:
f ‘(1/(nπ)) = 0
.
Ainsi, la limite n’existe pas, ce qui montre que f ‘ n’est pas continue en 0.
Exercice 7 :
Pour démontrer que est dérivable sur I et calculer sa dérivée, on peut utiliser la formule de dérivation d’une composition de fonctions.
On a pour tout x de I, et u et v sont dérivables sur leurs intervalles respectifs. En appliquant la formule de dérivation d’une composition de fonctions, on obtient:
,
car la dérivée de v en u(x) est v'(u(x)), et la dérivée de u en x est u'(x).
On peut également réécrire cette formule en utilisant la notation fonctionnelle u(x) = y pour obtenir:
.
En remplaçant y par u(x), on obtient la formule souhaitée:
.
Ainsi, la fonction vou est dérivable sur I, et sa dérivée en tout point x de I est donnée par la formule .
Exercice 8 :
Pour démontrer que les fonctions sinus et cosinus sont dérivables sur et préciser leur fonction dérivée, on peut utiliser la définition de la dérivée d’une fonction en un point ainsi que les propriétés des fonctions trigonométriques.
1. Dérivabilité de la fonction cosinus:
On doit montrer que la limite existe pour tout x de
.
En utilisant la formule de l’addition pour le cosinus, on peut écrire:
.
Ainsi, on a:
|cos(x+h) – cos(x)| ≤ 2|h|.
En divisant par h, on obtient:
pour tout h≠0.
En utilisant le théorème des gendarmes, on en déduit que la limite du quotient est nulle:
.
Ceci montre que la fonction cosinus est dérivable sur , et que sa fonction dérivée est
.
2. Dérivabilité de la fonction sinus:
On doit montrer que la limite existe pour tout x de
.
En utilisant la formule de l’addition pour le sinus, on peut écrire:
.
Ainsi, on a:
.
En divisant par h, on obtient:
pour tout h≠0.
En utilisant le théorème des gendarmes, on en déduit que la limite du quotient est nulle:
.
Ceci montre que la fonction sinus est dérivable sur , et que sa fonction dérivée est
.
Ainsi, les fonctions sinus et cosinus sont dérivables sur , et leur fonction dérivée est respectivement -sin(x) et cos(x).
Exercice 9 :
1. Pour démontrer que la fonction f est bornée sur , il suffit de trouver une constante M > 0 telle que |f(x)| ≤ M pour tout x de
.
Remarquons que |x|+1 est toujours strictement supérieur à 1, donc f sera bornée si et seulement si est bornée.
Pour x>0, on a: , car
.
De même, pour x<0, on a: , car
.
Ainsi, f est bornée sur par 1/2.
2. Pour étudier la parité de la fonction f, on doit vérifier si pour tout x de
.
On a: .
Ainsi, la fonction f est impaire.
3. Pour étudier la dérivabilité de la fonction f en 0, on doit calculer la limite du taux d’accroissement de f en 0.
On a:
,
donc
,
car 1+|x| est toujours supérieur ou égal à 1.
En divisant par |x| (qui est non nul), on obtient:
.
En utilisant le théorème des gendarmes, on en déduit que la limite du taux d’accroissement de f en 0 est égale à 0 :
.
Ainsi, f est dérivable en 0 et sa dérivée est f ‘(0) = 0.
4. Pour démontrer que f définit une bijection de sur ]-1;1[, on doit montrer que f est injective et surjective.
– Pour montrer l’injectivité, supposons que f(x) = f(y) pour deux réels x et y quelconques. Alors, on a:
.
En notant a = |x| et b = |y|, on peut réécrire l’équation précédente sous la forme :
x(1+b) = y(1+a),
et, comme x et y ont le même signe (sinon f(x) et f(y) seraient de signes opposés), on peut diviser les deux membres de l’équation par xy pour obtenir :
.
Remarquons maintenant que (1+b)/(1+a) est strictement positif (car x et y sont de meme signe).
Donc, pour que l’équation précédente soit vraie, il faut que y/x soit également positif, c’est-à-dire que x et y soient du même signe.
On peut alors diviser les deux membres de l’équation précédente par y/x, pour obtenir :
(1+b)/(1+a) = 1
soit encore
|y| = |x|.
Mais dans ce cas, on a nécessairement x = y (parce que x et y sont de même signe). Ainsi, on a bien montré que f est injective.
– Pour montrer la surjectivité, il suffit de montrer que tout réel z appartenant à ]-1,1[ est atteint par la fonction f, c’est-à-dire qu’il existe x dans tel que f(x) = z.
Comme f est impaire, on peut supposer sans perte de généralité que z est positif. Alors si on prend , on a :
.
Ainsi, f est surjective de sur ]-1;1[, et on a bien montré que f est une bijection entre ces deux ensembles.
Exercice 10 :
1. Pour étudier la limite de f en , on doit vérifier que l’on est en présence d’une forme indéterminée de la forme
ou
.
En effet, en , le dénominateur de f s’annule, donc on ne peut pas évaluer la limite directement.
Pour déterminer la limite, on peut utiliser l’accroissement moyen de cos(x) en .
On a:
,
donc
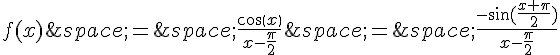
En effectuant le changement de variable , on peut réécrire f sous la forme:
,
avec lorsque
. Alors, on a :
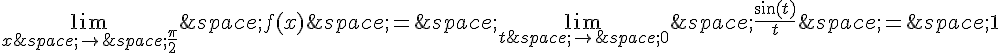
ce qui est une limite connue.
2. Pour la fonction , en a=0, on est également en présence d’une forme indéterminée de la forme 0/0.
En appliquant la formule avec
et b = 1, on peut réécrire f sous la forme :
.
Alors, on a :
.
Pour la fonction , en
, on est également en présence d’une forme indéterminée de la forme 0/0.
En appliquant la formule de l’arc tangente pour exprimer en fonction de
, on peut réécrire f sous la forme :
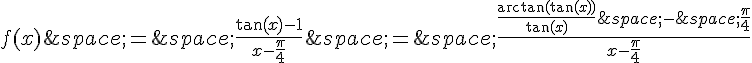
Alors, on a :
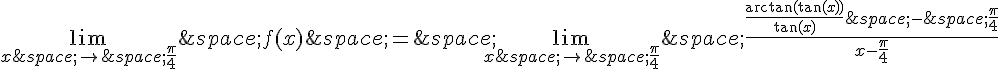
qui est également une forme indéterminée.
On peut utiliser la règle de L’Hôpital:
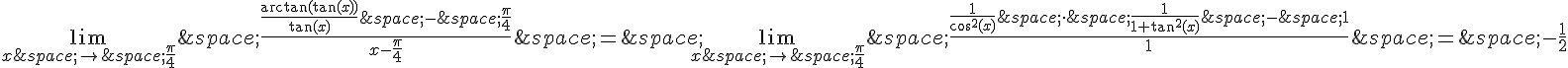
car et
.
Exercice 11 :
Soit la fonction f définie par :
f est dérivable sur en tant que polynôme .
Etudier la dérivée seconde puis la dérivée première et déduisez-en que f reste toujours strictement positive.
Exercice 12 :
1. Pour déterminer les limites de la fonction f en ,
et en
et
, on peut utiliser la forme asymptotique de f en
et
qui est la droite
Ainsi :
.
.
(car le dénominateur de la fraction tend vers 0-).
(car le dénominateur de la fraction tend vers 0+).
2. Pour démontrer que la droite d’équation y=x+3 est une asymptote oblique à Cf en
et
, on peut calculer la limite de la différence f(x) – (x+3) lorsque x tend vers
ou
.
On a :
Ainsi, on peut dire que la droite \Delta d’est une asymptote oblique de en
et
.
3. Pour calculer la fonction dérivée f’, on peut utiliser les règles de dérivation et la formule de dérivation d’une fraction. On a :
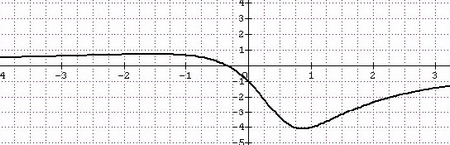
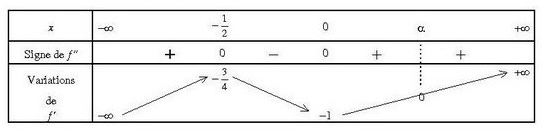
4. Pour dresser le tableau de variations de f, on peut utiliser le signe de la fonction dérivée f'(x) ainsi que les limites que l’on a déterminées précédemment. On obtient :
| x | – | 1^- | 1^+ | 4 | +
|
|——–|———|———–|———-|————|————–|
| f'(x) | + | – | + | + | + |
| f(x) | – | – | +
| 7 |
|
5. Pour déterminer l’équation de la tangente T à Cf au point d’abscisse , on peut utiliser la formule de la tangente T en un point d’une courbe y=f(x) :
Ainsi, avec , on a :
Or et
.
Ainsi, on a :
y + 6 = 8x
On peut réécrire cette équation sous la forme .
Ainsi, l’équation de la tangente T est .
Exercice 13 :
1. .
2. Donc f est croissante sur décroissante sur
et croissante sur
.
Exercice 14 :
Nous avons
Conclusion :
La fonction recherchée est telle que .
Exercice 15 :
1. La dérivée de est:
D’abord, appliquons la règle de la somme et de la différence pour les dérivées:
Ensuite, rassemblons les termes:
2. La dérivée de est:
D’abord, appliquons la règle de la fraction pour les dérivées:
Ensuite, rassemblons les termes:
3. La dérivée de est:
D’abord, appliquons la règle de la somme et de la différence pour les dérivées:
Ensuite, rassemblons les termes:
4. La dérivée de est:
D’abord, appliquons la règle de la chaîne pour les dérivées (en utilisant la fonction composite et
):
Ensuite, rassemblons les termes:
5. La dérivée de est:
D’abord, appliquons la règle de la chaîne pour les dérivées (en utilisant la fonction composite et
:
Ensuite, rassemblons les termes:
6. La dérivée de est:
D’abord, appliquons la règle de la chaîne pour les dérivées (en utilisant la fonction composée) et
:
Ensuite, rassemblons les termes:
Exercice 16 :
Pour démontrer qu’il existe deux réels R et tels que pour tout x de
:
,
on peut utiliser la méthode de la projection orthogonale.
La fonction est une fonction continue et périodique de période
.
On peut donc considérer le cercle trigonométrique et la projection orthogonale de f(x) sur l’axe des abscisses.
Cette projection est une fonction de la forme , où R est la longueur de la projection et
est l’angle entre la projection et l’axe des abscisses.
Pour trouver R et , on peut utiliser les propriétés trigonométriques.
La longueur de la projection est donnée par :
.
L’angle est donné par :
Pour résoudre l’équation , on remarque que cette équation peut être mise sous la forme
, où a = 1, b = 1 et
.
On a donc :
Les solutions de l’équation sont donc
ou
pour k
.
Exercice 17 :
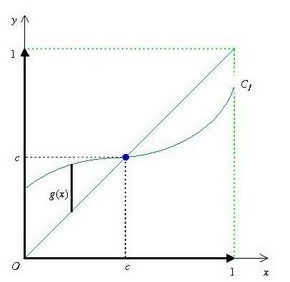
On peut démontrer que toute fonction continue de [0,1] dans [0,1] admet au moins un point fixe en utilisant le théorème du point fixe de Banach.
Soit f une fonction continue de [0,1] dans [0,1].
On pose g(x) = f(x) – x.
On remarque que et
, donc
.
Par conséquent, il existe un tel que
, c’est-à-dire
.
Ainsi, on a démontré que f admet au moins un point fixe dans [0,1].
Exercice 18 :
Pour démontrer que l’équation n’a pas de solution réelle, on peut utiliser différentes méthodes comme le théorème de Descartes, la règle des signes de Sturm ou le calcul de la dérivée de la fonction associée.
Voici une méthode utilisant la dérivée :
Soit .
Si f(x) avait une solution réelle, cette solution serait un zéro de f(x) et donc, f(x) = 0.
Considérons la dérivée de f(x) : .
Si x est une solution de f(x) = 0, alors x est également une solution de la fonction .
Supposons maintenant que x est une solution réelle de f(x) = 0.
Alors x est également une solution de g(x) = 0.
Or, il a été démontré en utilisant la règle des signes de Sturm que l’équation n’a pas de solution réelle.
Ceci est en contradiction avec notre supposition que x est une solution réelle de f(x) = 0.
Par conséquent, nous pouvons conclure que l’équation n’a pas de solution sur
.
Exercice 19 :
1. Pour démontrer que la somme de deux fonctions dérivables est dérivable, on utilise la définition de la dérivée en a :
= lim_{x->a} [f(x) – f(a)] / (x-a) + [g(x) – g(a)] / (x-a)
= f'(a) + g'(a)
Puisque les limites individuelles f'(a) et g'(a) existent, la limite de la somme existe également.
Donc, la fonction f+g est dérivable en a.
2. Pour démontrer que le produit de deux fonctions dérivables est dérivable, on utilise la formule du produit :
Puisque les limites individuelles et
existent, la limite de la somme existe également.
Donc, la fonction fg est dérivable en a.
3. Supposons que g est nulle au voisinage de a, c’est-à-dire qu’il existe un rayon tel que g(x) = 0 pour tout x dans l’intervalle ouvert
. Alors, pour x différent de a, on a :
Puisque g(x) est non nulle dans l’intervalle ouvert , on a que |g(x)| > 0 pour x dans cet intervalle, donc |g(a)| et |g(x)| sont bornés et non nuls, donc leur produit est borné et non nul également. Alors :
où M est une borne supérieure de .
Donc, en appliquant le critère de comparaison des suites à la limite de la dérivée, on a :
Donc, la fonction 1/g est dérivable en a.
Exercice 20 :
1. Pour étudier les limites de f en et en
, on peut utiliser la règle de l’hospital ou factoriser l’expression sous la racine :
La courbe n’a pas d’asymptotes horizontales car les limites en
et en
sont différentes.
2. Pour déterminer s’il existe une asymptote oblique à en
, on peut vérifier si la différence entre f(x) et la droite
tend vers zéro quand x tend vers
:
Donc, la droite est asymptote oblique à Cf en
.
Exercice 21 :
Pour chacune des fonctions f suivantes :
• Indiquer l’ensemble de dérivabilité de la fonction .
• ,Calculer sa dérivée .
a. .
f est dérivable sur
b. .
f est dérivable sur
c. .
f est dérivable sur
d. .
f est dérivable sur
e. .
f est dérivable sur
f. .
f est dérivable sur
g. .
f est dérivable sur
h. .
f est dérivable sur
Exercice 22 :
Pour tout entier naturel n, on considère la fonction définie sur
par :
• pour n=0,
• pour
On Désignera par la courbe représentative de
dans un repère orthonormal
ayant comme unité graphique 4 cm.
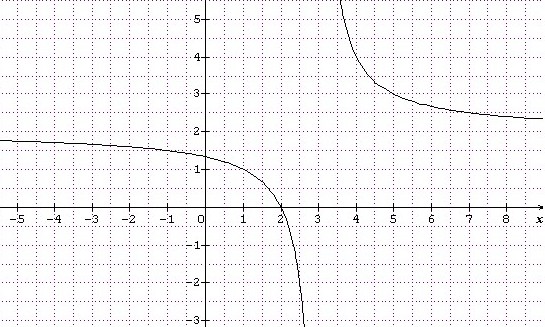
1. Déterminer les limites de aux bornes de son ensemble de définition.
Etudier le sens de variation de et construire
dans le repère
.
Soit
f ‘ est négative et f est donc croissante sur
2. Soit n un entier naturel non nul.
a. désignant la fonction dérivée de
, montrer que :
A montrer par récurrence.
b. Etudier le sens de variation des fonctions et
puis dresser leur tableau de variation .
c. Tracer et
dans le repère
.
Exercice 23 :
Calculer les limites suivantes, dont on admettra l’existence.
a. .
b. .
c. .
d. .
e. .
f. .
Exercice 24 :
Pour chacune des fonctions f suivantes :
• Déterminer son ensemble de définition.
• Calculer les limites aux bornes de son domaine de définition.
• En déduire l’existence d’asymptote à la courbes représentative de la fonction f et indiquer leur équation .
a. .
f est définie sur
Il y a une asymptote verticale d’équation x=3 et une horizontale d’équation y=2 .
b. .
f est définie
donc f est définie sur .
Il y a deux asymptotes verticales d’équation x=-3 et x=4 et une horizontale d’équation y=4 .
Exercice 25 :
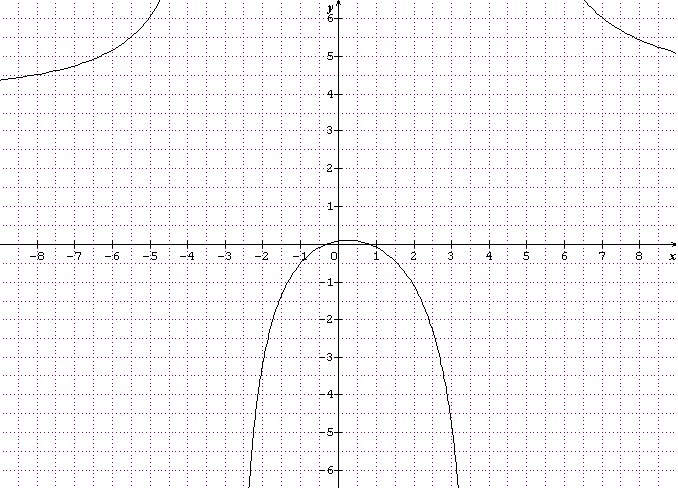
1. Etudier la restriction de f à l’intervalle [0;2] et construire la courbe représentative de
.
est dérivable sur [0;2[ en tant que fonction polynomiale.
donc f ‘ est positive et f est croissante sur
Comment peut-on en déduire la courbe représentative de la restriction de f à l’intervalle où n est élément de
.
f est 2-périodique donc il suffit de translater la courbe de f de 2 unités horizontalement.
2. Démontrer que :
Si
Utilisons le principe de récurrence :
soit la propriété :
Initialisation :
donc P(0) est vraie.
Supposons qu’il existe
Montrons que P(n+1) reste vraie.
Soit
Posons x=X+2
alors
et
Donc P(n+1) reste vraie.
Conclusion :
3. Est-ce que f est continue sur ?
Oui elle est continue sur R et on peut poser f(2n)=0 en prolongement par continuité.
4. Est-ce que f est dérivable sur ?
Elle est dérivable également sur R.
Exercice 26 :
1.
2.
Donc f est strictement croissante sur
3. L’équation de la tangente en est donnée par :
et
donc
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «dérivée d’une fonction : corrigé des exercices de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.



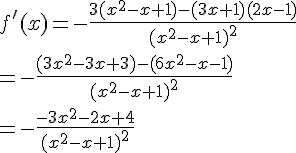
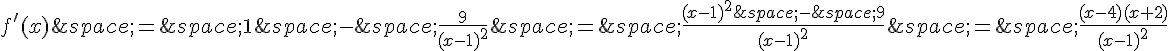
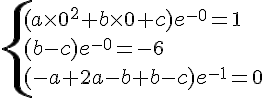
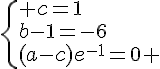
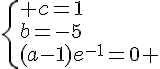
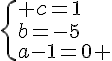
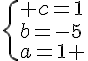
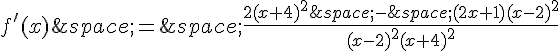
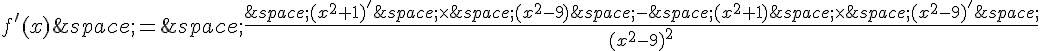
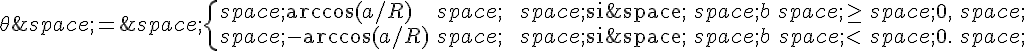
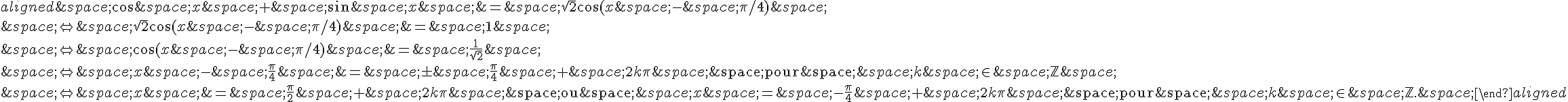
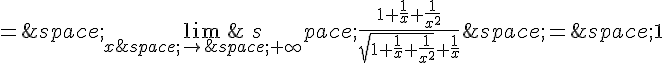
![\lim_{x\,\to\,-\infty}\,[f(x)\,-\,(-2x-\frac{1}{2})]\\,=\,\lim_{x\to-\infty}\,(\sqrt{x^2+x+1}-x+2x+\frac{1}{2})\,\=\,\lim_{x\to-\infty}\,(\sqrt{x^2+x+1}+x+\frac{1}{2})](https://mathovore.fr/latex-images/5f512b2b788580c6355681bdda5e3187.png)