Probabilités : exercices de maths en 3ème corrigés en PDF.

Mis à jour le 28 mai 2025

---

Exercice 1 – Arbre de probabilité

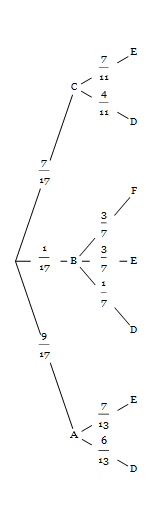
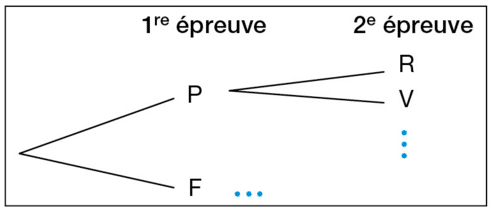
L’arbre ci-dessous donne les probabilités associées à une expérience aléatoire à deux épreuves.
A, B, C, D, E, F sont six événements susceptibles d’être réalisés lors d’une des deux épreuves.

Déterminez la probabilité p que l’événement D soit réalisé à la deuxième épreuve sachant que l’événement A est réalisé à la première épreuve.

Exercice 2 – Tirer une boule de couleur

Une urne contient 3 boules de couleur noire, 9 boules de couleur blanche, 2 boules de couleur rouge, 1 boule de couleur verte, indiscernables au toucher.
On tire au hasard une boule de cette urne.

La probabilité de tirer une boule de couleur verte est ?

Exercice 3 – Problème d’une urne

Dans une urne, il y a deux boules vertes (V) , 5 boules oranges (O)

et trois boules bleues (B) , indiscernables au toucher.

On tire successivement et sans remise deux boules.

1. Quelle est la probabilité de tirer une boule orange au premier tirage ?

2. Construire un arbre des probabilités décrivant l’expérience aléatoire.

3. Quelle est la probabilité que la première boule soit bleue et la deuxième soit orange ?

4. Quelle est la probabilité que la deuxième soit verte ?

Exercice 4 – Tourner une roue

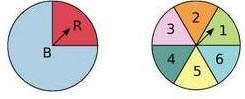
Dans un jeu, on doit tourner deux roues. La première roue donne une couleur : bleu, avec la probabilité , ou rouge.

La deuxième roue donne un chiffre entre 1 et 6 avec la même probabilité.

a. Si après avoir tourné les roues, les aiguilles se trouvent comme sur le schéma, on note (R,1) le résultat obtenu.

a. Quelle est la probabilité d’obtenir << Rouge>> avec la première roue ?

b. Quelle est la probabilité d’obtenir chacun des chiffres avec la deuxième roue ?

c. Construire et compléter un arbre représentant les différents résultats possibles.

d. quelle est la probabilité du résultat (R,1) ?

e. Quelle est la probabilité du résultat (B,4) ?

f. Quelle est la probabilité d’obtenir << et un chiffre pair ?

g. Quelle est la probabilité d’obtenir <> ou un chiffre pair ?

Exercice 5 – Boules indiscernables

Une urne contient 7 boules indiscernables au toucher : 4 boules bleues et 3 boules rouges .
a)On tire successivement et avec remise 2 boules de l’urne .

Calculer les probabilités que :
la première boule soit bleue et la seconde soit rouge
les deux boules aient la même couleur
b)Reprendre la question précédente en supposant que le tirage est sans remise.
c) Reprendre les questions précédentes en supposant que l’urne contienne aussi 2 boules noires.

Exercice 6 – Résidence de vacances

Une résidence de vacance propose deux types d’appartements ( studio et deux-pièces ) à louer. L’appartement doit-être restitué parfaitement propre en fin de séjour.
Le locataire peut décider de nettoyer lui- même ou peut choisir l’une des deux formules suivantes : la formule  » simple  » ( nettoyage de l’appartement en fin de séjour par le personnel d’entretien) ou la formule  » confort » ( nettoyage quotidien du logement et nettoyage complet en fin de séjour par le personnel d’entretien).
Le gestionnaire a constaté que :
– 60% des locataires optent pour un studio et, parmi ceux-ci, 20% ne souscrivent aucune formule d’entretien.
– La formule  » simple  » a beaucoup de succès : elle est choisit par 45% des locataires de studio et par 55% des locataires de deux pièces.
On rencontre un résident au hasard.
1) Traduire l’énoncé à l’aide d’un arbre pondéré.
2) La personne rencontré a loué un studio ? Quelle est la probabilité qu’elle ait souscrit la formule  » confort  » ?
3)a) Calculer la probabilité que la personne rencontrée loue un studio et n’ait souscrit aucune formule ?
b) On sait de plus que 18% des locataires ne souscrivent aucune formule. Le résident rencontré loue un deux pièces. Montrer que la probabilité qu’il assure lui-même le nettoyage de son appartement est 0.15 !

Exercice 7 – Billet de loterie

120 spectateurs assistent a une séance de cinéma. A l’entrée on a distribue
*3 de ces billets donnent droits a 4 places gratuites
*6 donnent droit a 3 places gratuites
*18 donnent droit a 2 places gratuites
*42 donnent droit a 1 place gratuite
* les autres billets ne gagnent rien
on donnera les réponses sous formes de fractions irréductibles.
1-Quelle est la probabilité pour 1 spectateur.
a)de gagner exactement 2 places gratuites.
b)de ne rien gagner.

2-dessiner l’arbre des possibilités pondérées par les probabilités .

3-a)Quelle est la probabilités pour un spectateur de gagner 3 ou 4 places gratuites?
b)Calculer de 2 façons différents la probabilités pour un spectateur de gagner au moins 2 places gratuites.

Exercice 8 – Une urne contenant quatre boules

Une urne contient quatre boules numérotées de 1 à 4 , On tire une boule au hasard, on note son numéro, et on la remet dans l’urne.

On tire a nouveau au hasard une boule de l’urne et on note a nouveau son numéro . Le résultat de l’expérience est un nombre a deux chiffres , par exemple si on tire 3 au premier tirage et 2 au second , le résultat obtenu est 32.

1a) Déterminer à l’aide d’un arbre toutes les issues possibles pour cette expérience à deux épreuves.

b-Pondérer l’arbre obtenu

2- Reprendre les questions précédentes mais cette fois on ne remet pas la boule dans l’urne après le premier tirage.

Exercice 9 – Problème de l’urne et des boules

On considère l’urne contenant les boules ci contre (l’urne contient 14 boules dont 5 boules de 1, 6 boules de 2, et 3 boules de 3)
1. on tire au hasard une boule et on regarde le numéro inscrit.
a) Citer les issues de cette expérience. ont-elles autant de chance de se réaliser?
b) déterminer la probabilité de l’événement A: « la boule porte le numéro 1″
2. On tire au hasard une boule et on regarde la couleur.
a) citer les issues de cette expérience. Ont-elles autant de chance de se réaliser?
b) Déterminer la probabilité de l’événement B: »‘la boule est grise »
3. On tire au hasard une boule et on regarde le numéro et la couleur.
a) Déterminer la probabilité de l’événement C: »la boule est verte et porte le numéro 1″
b) On sait que l’on tire une boule bleue. quelle est la probabilité qu’elle porte le numéro 2?

Exercice 10 – Sac contenant des lettres

Dans un sac contenant des lettres pour jouer au scrabble, on trouve 15 consonnes et 10 voyelles.
On effectue un premier tirage puis un second tirage  sans remettre la lettre tirée dans le sac .
1) Quelle est la probabilité d’obtenir une voyelle au premier tirage ?
2) Quelle est la probabilité d’obtenir un voyelle au second tirage quand on en a déjà eu une au premier tirage ?
3) Quelle est la probabilité d’obtenir une consonne au second tirage quand on en eu une voyelle au premier tirage ?
4) Quelle est la probabilité d’obtenir deux voyelles ?

Exercice 11 – Bouton

En appuyant sur un bouton, l’une des cases de cette grille s’allume:
1 Quelle est la probabilité que s’allume:
a)la case 1?
b)une case impaire?
c)une case portant un numéro supérieur ou égal a 6?
2. Quels sont les événements contraires de chacun des 3  événements ci-dessus?
Indiquer ensuite leurs probabilités.
3. Les cases 1 et 7 sont restées allumées.

Une 3ème case doit s’allumer.
a)Quelle est la probabilité que les 3 cases soient alignées?
b)Quelle est la probabilité que les 3 cases ne soient pas alignées?

Exercice 12 – Probabilités et statistiques

on lance un dé équilibré à dix faces (numéroté de 1 a 10) Si on obtient un nombre   premier alors on gagne 3€ , Sinon on  perd 2 € on relance le dé une 2ème fois puis une 3ème fois

a) détermine la liste des gain et des pertes possible pour ce jeu puis calcule la probabilité associée à chaque gain et à chaque perte .

b) En utilisant les réponses précédentes déterminer si on a intérêt à jouer a ce jeu.

Exercice 13 – Lancé de dés

On lance trois des a 6 faces. On calcule la somme de leur face supérieur .
A: Les trois des sont identiques
1) Déterminer tous les lancers pour lesquels on obtient une somme de 9 . (Je suppose qu’il faut faire un tableau?)
2) Déterminer tous les lancers pour lesquels on obtient une somme de 10 (pareil ?)
3) Sans tenir compte de l’ordre des des , y’a-t-il plus de façons d’obtenir une somme de 10 qu’une somme de 9 ? (je comprends pas du tout)

B: Les trois des sont des couleurs différentes
un des rouge , vert , bleu
1) Déterminer le nombre de lancers pour lesquels on obtient :
a)trois trois et trois
b)un quatre quatre
c)un deux six
(comprend pas du tout )
2) En déduire le nombre total de lancers pour lesquels on obtient une somme de 9
3) calculer de même le nombre de lancers pour lesquels on obtient une somme de 1o
4)En tenant compte de l’ordre des des y a-t-il plus de façons d’obtenir une somme de 10 q’une somme de 1O ?

Exercice 14 – Variété française

7 chansons de variété française (vf),3 titre de rap (r),4 variété international (vi) et 6 de jazz.

Dessiner l’arbre des possibilités pondérées par les probabilité écrite sous forme de fraction irréductible.

Calcule la probabilité de l’événement E : »Le titre diffusé n’est pas du jazz  »

Exercice 15 – Probabilités dans une urne

Exercice 16 – Problème de la roue et de la loterie

Exercice 17 :

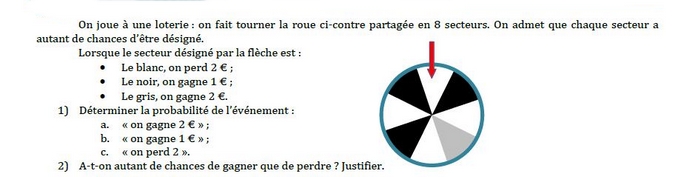
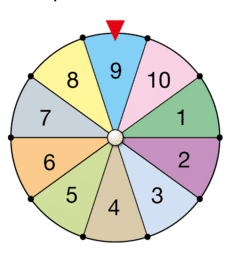
La roue de loterie ci-dessous est équilibrée et partagée en huit secteurs identiques.

On fait tourner la roue et on observe le numéro repéré.

Expliquer pourquoi l’événement E : « Le numéro repéré est divisible par 4 » et son événement
contraire ont la même probabilité.

Exercice 18 :

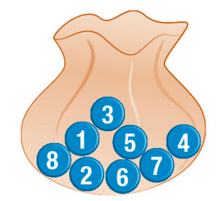
Un sac opaque contient huit jetons numérotés de 1 à 8.

On tire au hasard un jeton et on note son numéro.

1.Dans chaque cas, indiquer les issues qui réalisent
l’événement :

a. : « Obtenir un multiple de 2 »;

b.: « Obtenir un nombre supérieur ou égal à 4 »;
c.  : « Obtenir un nombre pair supérieur ou égal à 4 ».

2.Donner l’écriture décimale de chaque probabilité.
a. P() b. P() c.P()

Exercice 19 :

On tire au hasard une carte dans un jeu de 32 cartes.

1.a. Combien l’expérience compte-t-elle d’issues ?
b. Quelle est la probabilité de chaque issue ?

2.a. Indiquer les issues qui réalisent chacun des événements:

• E:« La couleur de la carte tirée est rouge (cœur ou carreau) » ;
• F:«La carte tirée est un as ».

b. Donner la probabilité de chacun de ces événements.

3.Existe-t-il des issues qui réalisent les deux événements E et F en même temps ?
Quelles sont-elles ?

Exercice 20 :

La roue équilibrée ci-dessous est partagée en dix secteurs identiques numérotés de 1 à 10.

Léa fait tourner la roue et observe le numéro repéré.
Elle s’intéresse aux événements suivants :

• E:«Le numéro repéré est pair »;
• F:«Le numéro repéré est multiple de 3»;
• G:« Le numéro repéré est multiple de 5 ».

1. Dresser la liste des issues qui réalisent chacun des événements E, F et G.

2.Dans chaque cas, dire si les événements sont incompatibles ou non. Justifier la réponse.
a. E  et  F     b. E  et  G     c. F  et  G

3.Donner la probabilité de chacun des événements E, F et G.

Exercice 21 :

Mathis lance une pièce équilibrée de 1€, note le résultat :
Pile (P) ou Face (F), puis tire au hasard une boule du sac et observe sa couleur : rouge (R), vert (V),
bleu (B), noir (N) ou jaune (J).

1. a. Recopier et compléter l’arbre ci-dessous.

b. Combien l’expérience compte-t-elle d’issues ?

2.Donner la probabilité de chacun des événements :

• : « Obtenir la couleur rouge »;
• :« Ne pas obtenir la couleur jaune ».

Exercice 22 :

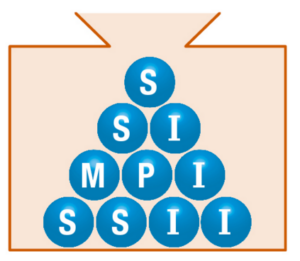
Une urne opaque contient dix boules.

Sur chacune d’elles est inscrite une des lettres du mot : MISSISSIPI.
On tire une boule au hasard de l’urne et on lit la lettre obtenue.

a. Dessiner l’arbre des issues pondéré par les probabilités écrites sous forme de fractions irréductibles.
b. Calculer la probabilité de l’événement E : « La lettre obtenue n’est pas une voyelle ».

Exercice 23 :

Un commerçant propose des boissons sur un marché.
Dans son réfrigérateur, on trouve 30 bouteilles de thé glacé (T),

32 de jus d’ananas (J), 18 de soda (S) et 40 d’eau gazeuse (E).
Ces bouteilles sont de même forme.
Le commerçant prélève au hasard une bouteille dans son réfrigérateur.
a. Dessiner l’arbre des issues pondéré par les probabilités écrites sous forme de fractions irréductibles.
b. Calculer la probabilité de l’événement E: « La bouteille n’est pas une bouteille d’eau gazeuse ».

Exercice 24 :

Tania lance au hasard un dé dont les faces sont numérotées de 1 à 6.

Elle lit le numéro sorti.
E est l’événement : « Tania lit un nombre pair ».
Citer les issues qui réalisent E, puis celles qui réalisent son événement contraire .

Exercice 25 :

On lance deux fois de suite une pièce de monnaie.
On note E l’événement : « Obtenir au moins une fois Pile ».
Énoncer l'(les) issue(s) qui réalise(nt) l’événement contraire de E.

Exercice 26 :

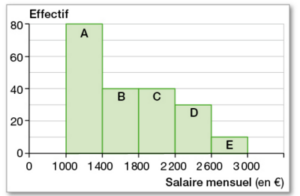
Voici la répartition des salaires dans une entreprise.
On compte cinq catégories de salaires : A, B, C, D et E.

Par exemple, un salarié de la catégorie A touche un salaire mensuel compris

entre 1 000 € inclus et 1 400 € exclu.
On rencontre au hasard un salarié de l’entreprise et
on lui demande sa catégorie de salaire.
a. Dessiner l’arbre des issues pondéré par les probabilités écrites sous forme

de fractions irréductibles.
b. Donner la probabilité de chacun des événements :
• U : « Le salarié gagne au moins 1 800 € par mois » ;
• V : « Le salarié gagne strictement moins de 2 200 €
par mois ».

Exercice 27 :

On lance deux fois de suite un dé équilibré a quatre faces numérotées de 1
à 4.
:
On repère à chaque lancer le numéro qui figure sur la face cachée du dé.

1 .a. Dessiner un arbre afin d’obtenir toutes les issues de l’expérience.
b. Quelle est la probabilité de chaque issue ?
2.a. Donner les issues qui réalisent l’événement :
E : « La somme des deux numéros est égale à 5 ».
b. Quelle est la probabilité de cet événement ?
3. Que dire de chaque événement ?
a. F : « La somme des deux numéros est égale à 1 ».
b. G : « La somme des deux numéros est inférieure à 10».

Exercice 28 :

Dans son dressing, Sarah possède quatre robes (une blanche, une noire, une rouge et une bleue) et
deux chapeaux (un rouge et un bleu).
Ce matin, elle choisit au hasard une robe et un chapeau.

a. Dessiner un arbre afin d’obtenir toutes les issues de l’expérience.
b. E est l’événement : « Sarah a choisi une robe et un chapeau de la même couleur ».
Quelle est la probabilité de cet événement ?
c. Définir l’événement contraire de E et calculer sa probabilité.

Exercice 29 :

Sur chacun des morceaux de papier représentés
ci-dessous, Antoine a écrit une lettre du mot ROSE.

Il place ces morceaux de papier dans un sac, puis il
tire au hasard un 1er morceau de papier, le remet dans
le sac et tire un 2e morceau de papier. Il lit les lettres obtenues.
1 .a. Dessiner un arbre afin d’énumérer les issues de l’expérience.
b. Quelle est la probabilité de chaque issue ?
2. Antoine s’intéresse à l’événement :
M : « J’ai tiré au moins une fois la lettre O ».
a. Définir l’événement contraire de M.
b. Donner la probabilité de l’événement .
c. En déduire la probabilité de l’événement M.
d. Retrouver la probabilité P(M) d’une autre façon.

Exercice 30 :

On écrit sur les faces d’un dé équilibré chacune des lettres du mot ARMURE.
On lance ce dé et on lit la lettre inscrite sur la face supérieure.

l. a. Quelles sont les issues de cette expérience ?
b. Donner la probabilité de chacune d’elles.
2. Déterminer la probabilité de l’événement :
a.  : « Obtenir une lettre du mot RAMEUR » ;
b.  : « Obtenir une lettre du mot COTON » ;
c. : « Obtenir une lettre du mot MALIN » ;
d.  : « Obtenir une consonne ».

Exercice 31 :

---

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «probabilités : exercices de maths en 3ème corrigés en PDF.» au format PDF.

     

---

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

---

OK

 Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.