Probabilités : cours de maths en 3ème à télécharger en PDF.

Les mathématiques sont considérées comme la matière où les élèves rencontrent le plus de difficultés. Mathovore vous permet de travailler sur probabilités : cours de maths en 3ème et réviser en ligne par le biais de milliers de ressources rédigées par une équipe d'enseignants volontaires de l'éducation nationale. Vous développerez vos connaissances autant dans le domaine de l'algébre qu'en géométrie. Les mêmes ressources que vous trouverez dans votre manuel scolaire avec des cours complets conformes aux programmes officiels de l'éducation nationale et des exercices corrigés poortant sur chaque chapitre du programme de votre niveau. Chaque document dispose, en bas de page, d'un lien vous permettant de l'exporter au format PDF. Oubliez les cours particuliers qui peuvent être très cher sur une année scolaire. Nos resssources, cours et exercices corrigés sur probabilités : cours de maths en 3ème vous permettent de vous exercer en ligne afin de combler vos lacunes en maths et d'envisager une constante progression tout au long de l'année scolaire en développant de nouvelles compétences et en comblant les différentes lacunes que vous rencontrez sur les cours de maths en 3ème . De nombreuses ressources en ligne pour les élèves de primaire (CE2, CM1 et CM1), du collège (6ème, 5ème, 4ème et 3ème) et du lycée (2de, 1ère et terminale) ainsi que de nombreux sujets du brevet des collèges et du baccalauréat afin de vous préparer dans les meileurs conditions pour ces diplômes. Les membres du site ont accès gratuitement aux différents corrigés afin de pouvoir relever les différents erreurs commises sur probabilités : cours de maths en 3ème et d'assimiler les différentes notions comme les définitions, les propriétés et les théorèmes.

Sommaire de cette fiche

1 I. Notion de probabilité
2 II.Expérience à deux épreuves

Les probabilités dans un cours de maths en 3ème où nous étudierons la définition d’une probabilité ainsi que la notion d’ensemble et d’expérience aléatoire. Nous verrons les différents événements impossible, contraires ou incompatibles. Dans cette leçon en troisième, nous tracerons des arbres de probabilités à une ou deux épreuves.

I. Notion de probabilité

1.Issues et arbre de probabilité

Définition :

Lorsqu’on effectue une expérience aléatoire, on ne peut pas prévoir à l’avance quel va être son résultat, parmi les différentes issues possibles.

Un arbre de probabilité est un schéma permettant de visualiser les différentes issues d’une expérience aléatoire..Sur chaque branche menant à une issue, on indique la probabilité de cette issue.

On dit que l’arbre est pondéré par les probabilités.

Exemple :

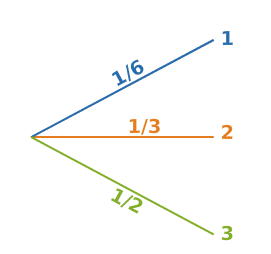
Katia lance un dé équilibré à six faces numérotées 1, 2, 2, 3, 3 et 3.On observe le nombre indiqué sur la face supérieure : les issues sont 1, 2 et 3.Le dé est équilibré, donc chaque face a autant de chance de sortir qu’une autre.

$\star\,$ Ainsi, la probabilité de sortie du nombre 1 est de $\frac{1}{6}$ , puisqu’une seule face du dé porte le numéro 1.

$\star\,$ Deux faces portent le nombre 2, donc la probabilité de l’issue 2 est de $\frac{2}{6}$ soit $\frac{1}{3}$ .

$\star\,$ De même, celle de l’issue 3 est $\frac{3}{6}$ soit $\frac{1}{2}$ soit encore 0,5 ou 50 %.

On résume ces résultats sur l’arbre de probabilité ci-dessous.

Propriété :

Une probabilité est un nombre compris entre 0 et 1.Elle peut être exprimée par un nombre en écriture fractionnaire, en écriture décimale, ou bien encore sous forme d’un pourcentage.

2.Evénements

Définition :

Un événement réalisé par aucune issue est appelé événement impossible.Sa probabilité est 0.
Un événement réalisé par toute issue de l’expérience est appelé événement incertain.

Sa probabilité est 1.

$\star\,$ L’événement contraire d’un événement A est l’événement, noté $\overline{A}$ , qui est réalisé lorsque A n’est pas réalisé.

Propriété :

$\star\,$ La probabilité d’un événement est la somme des probabilités des issues qui le réalisent. $\star\,$ La somme des probabilités d’un événement et de son contraire est égale à 1.

Nous avons $P(A)+P(\overline{A})=1$ .

Exemple :

Reprenons le dé de Katia.

L’événement « obtenir un multiple de 5 » est un événement impossible.
L’événement « obtenir un nombre à un chiffre » est un événement certain.
L’événement « obtenir un nombre impair » est réalisé par les issues 1 et 3.

Sa probabilité est donc $\frac{1}{6}+\frac{1}{2}=\frac{1}{6}+\frac{3}{6}=\frac{4}{6}=\frac{2}{3}$ .

On en déduit que la probabilité de l’événement contraire « obtenir un nombre pair » est de $\frac{1}{3}$ .

Définition :

Deux événements sont dits incompatibles lorsqu’ils ne peuvent pas se réaliser simultanément.

Exemple :

Avec le dé de Katia, l’événement « obtenir un nombre pair » et l’événement « obtenir 3 » sont incompatible.

3.Des fréquences aux probabilités

Lorsque aucune considération de régularité ou de symétrie ne permet de connaître la probabilité d’une issue, on peut l’estimer en effectuant un grand nombre de fois une expérience aléatoire.

Propriété :

On considère une expérience aléatoire et un événement A dont la probabilité est notée P(A).Lorsqu’on répète un grand nombre de fois cette expérience aléatoire, la fréquence d’apparition de l’événement A a tendance à se stabiliser autour du nombre P(A).

Exemple :

En lançant un grand nombre de fois un bouchon de la même façon, on pourrait ainsi estimer la probabilité qu’il retombe dans l’une ou l’autre des positions ci-dessous.

II.Expérience à deux épreuves

Propriété :

Sur un arbre de probabilité illustrant une expérience aléatoire à deux épreuves, la probabilité d’une issue est obtenue en multipliant les probabilités rencontrées sur les branches du chemin de l’arbre menant à cette issue.

Exemple :

On lance une pièce de monnaie équilibrée, puis ensuite on lance le dé de Katia.

On note P l’événement « la pièce tombe sur pile » et F « la pièce tombe sur face ».

L’arbre de probabilité permet de visualiser les six issues de cette expérience aléatoire à deux épreuves.

La probabilité que la pièce tombe sur face, puis que le dé tombe sur 1, notée (F;1) est donnée par le chemin de l’arbre représentant cette issue.

Elle est donc égale au produit $\frac{1}{2}\times \,\frac{1}{6}$ , soit $\frac{1}{12}$ .

4.1/5 - (33 votes)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «probabilités : cours de maths en 3ème» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés.

D'autres fiches similaires à probabilités : cours de maths en 3ème.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à probabilités : cours de maths en 3ème à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème probabilités : cours de maths en 3ème, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Probabilités : exercices de maths en 3ème corrigés en PDF.
55
Des exercices sur les probabilités en troisième (3ème) à télécharger gratuitement en PDF. Exercice 1 - Arbre de probabilité L'arbre ci-dessous donne les probabilités associées à une expérience aléatoire à deux épreuves. A, B, C, D, E, F sont six événements susceptibles d'être réalisés lors d'une des deux épreuves. Déterminez…

Les dernières fiches mises à jour

Voici les dernières ressources mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 2 493 871 cours et exercices de maths téléchargés en PDF et 184 557 membres.
Rejoignez-nous : inscription gratuite.