Voici le sujet de mathématiques du brevet France 2025, donné aux élèves de troisième en série générale lors de la session de juin, suivi de sa correction complète rédigée directement sous l’énoncé. L’épreuve dure deux heures, est notée sur 100 points et comporte cinq exercices indépendants.
Le premier exercice porte sur les probabilités avec deux urnes, les nombres premiers et les multiples. Ensuite, le deuxième, consacré à un aquathlon, fait appel au théorème de Pythagore, à la réciproque du théorème de Thalès, à la trigonométrie, puis à la médiane d’une série de temps et à un calcul de vitesse. Par ailleurs, le troisième est un QCM de six questions : proportionnalité, transformations, pourcentage, aire, développement et volume d’une pyramide. Puis le quatrième compare deux programmes de calcul, dont un script Scratch, et le dernier confronte deux offres d’un garage à l’aide d’un tableur et de fonctions affines.
Pour vous entraîner dans les conditions de l’examen, traitez l’épreuve en temps limité avec la calculatrice en mode examen, puis comparez votre copie au corrigé détaillé en bas de page, où chaque réponse est justifiée. Ensuite, le sujet est aussi proposé en PDF à imprimer.
L’essentiel : Corrigé du brevet de maths France 2025, avec : chaque question est résolue avec les calculs et la méthode attendue. Idéal pour réviser l’examen en se corrigeant ; corrigé gratuit en PDF.
DIPLÔME NATIONAL DU BREVET
FRANCE SESSION 2025
MATHEMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 100 points
Exercice 1 (20 points) (brevet France 2025)
On dispose d’une urne A contenant 6 boules numérotées : 7 ; 10 ; 12 ; 15 ; 24 ; 30
et d’une urne B contenant 9 boules numérotées : 2 ; 5 ; 6 ; 8 ; 17 ; 18 ; 21 ; 22 ; 25.
Les boules sont indiscernables au toucher.
1. On tire une boule dans l’urne A, quelle est la probabilité d’obtenir un nombre pair ?
2. On tire une boule dans l’urne B, justifier que la probabilité d’obtenir un nombre premier est de 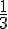\(\frac{1}{3}\).
3. Quelle urne contient le plus grand nombre de boules dont le numéro est un multiple de 6 ?
4. On tire une boule au hasard dans l’une des urnes.
Démontrer que la probabilité d’obtenir un nombre supérieur ou égal à 20 est la même quelle que soit l’urne choisie ?
5. En repartant avec la composition initiale des urnes A et B on décide d’ajouter une boule
numérotée 50 dans chacune d’entre elles. Dans ces conditions, la probabilité d’obtenir un
résultat supérieur ou égal à 20 est-elle toujours égale quelle que soit l’urne choisie ?
Exercice 2 (23 points)
Cette année, les professeurs d’EPS proposent aux élèves un aquathlon (course à pied et natation).
Partie A : La course à pied
Le parcours de la course à pied est représenté par le dessin ci-dessous (le dessin n’est pas à
l’échelle) :
Le parcours est représenté par ACDEB avec le départ au point A et l’arrivée au point B.
Les points A, C, B sont alignés.
Les points A, D, E sont alignés.
ADC est un triangle rectangle en A.
AC = 480 m CB = 120 m
AE = 250 m DE = 50 m
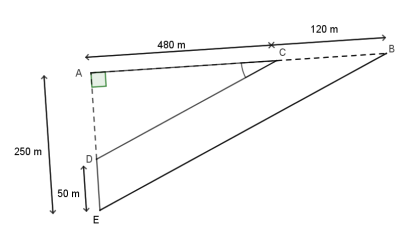
1. Justifier que AD = 200 m.
2. Calculer la longueur CD.
3. Pour que le parcours soit validé il est nécessaire que les droites (CD) et (BE) soient parallèles et
que la mesure de l’angle 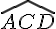\(\widehat{ACD}\) soit supérieure à 20°.
a. Les droites (CD) et (BE) sont-elles parallèles ?
b. La mesure de l’angle 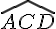\(\widehat{ACD}\) est-elle supérieure à 20° ?
c. Le parcours est-il validé ?
Partie B : La natation
Concernant l’épreuve de natation, il s’agit de nager une distance de 200 m.
Voici les temps de 9 élèves :
5 min 30 s ; 5 min 45 s ; 5 min 49 s ; 5 min 50 s ; 6 min ; 6 min 11 s ; 6 min 12 s ; 6 min 20 s ; 6 min 40 s.
4. Quel est le temps médian de cette série ?
5. Un poisson rouge nage à la vitesse de 5 km/h. Nage-t-il plus vite que l’élève le plus rapide ?
Exercice 3 (18 points) (brevet France 2025)
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n’est demandée.
Pour chaque question, quatre réponses (A, B, C ou D) sont proposées.
Une seule réponse est exacte. Recopier sur la copie le numéro de la question et la lettre
correspondant à la réponse exacte.
Question 1
Le prix de 3 melons est 8,40 €. Combien coûtent 5 melons ?
| A | B | C | D |
| 16,40 € | 42 € | 14 € | 10,40 € |
Question 2
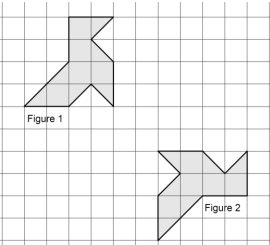
Quelle transformation permet de passer de la figure 1 à la figure 2 ?
| A | B | C | D |
| Une symétrie centrale | Une rotation | Une translation | Une symétrie axiale |
Question 3
Un article coûte 350 €. Son prix augmente de 20 %. Quel est son nouveau prix ?
| A | B | C | D |
| 420 € | 330 € | 370 € | 280 € |
Question 4
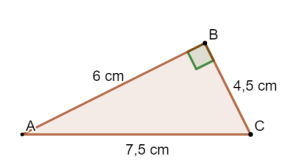
Quelle est l’aire du triangle rectangle ABC ?
| A | B | C | D |
| 27 cm² | 13,5 cm² | 18 cm² | 9 cm² |
Question 5
Quelle est la forme développée et réduite de l’expression \((2x+3)(x-4)\) ?
| A | B | C | D |
| \(2x^2-5x-12\) | \(2x^2-11x-12\) | \(2x^2-12\) | \(3x-1\) |
Question 6
Quel est le volume de cette pyramide à base rectangulaire ?
| A | B | C | D |
| 23 cm³ | 112 cm³ | 336 cm³ | 168 cm³ |
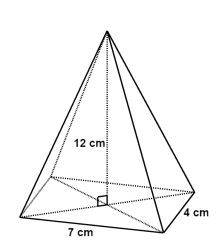
Exercice 4 (20 points)
Au club « Mathsetmagie », on s’amuse à créer des programmes de calcul plus ou moins magiques.
Partie A : Le programme de Zoé
Voici le programme de calcul de Zoé :
Programme de Zoé :
- Choisir un nombre
- Soustraire 4
- Multiplier par 2
- Ajouter 8.
1. Vérifier que si on choisit 10 comme nombre de départ, on obtient 20 avec ce programme.
2. Quel résultat obtient-on avec ce programme si on choisit −7 comme nombre de départ ?
3. Zoé prétend que son programme est « magique » car, quel que soit le nombre choisi, le résultat est toujours le double du nombre de départ.
A-t-elle raison ?
Partie B : Le programme de Fred
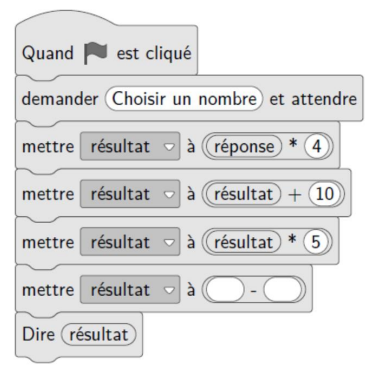
Fred décide de faire son programme de calcul sur Scratch :
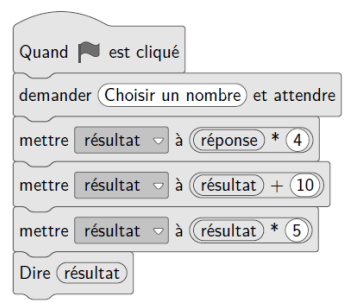
4. Démontrer que si le nombre de départ est x, le résultat obtenu avec le programme de Fred est 20x + 50.
5. Quel nombre faut-il choisir au départ pour obtenir 75 avec le programme de Fred ?
6. Constatant que son programme n’a rien de magique, Fred souhaite le modifier afin que le résultat soit toujours 20 fois plus grand que le nombre de départ.
Recopier et compléter sur la copie la sixième ligne du programme pour que ce soit le cas.
Exercice 5 (19 points) (brevet France 2025)
Un garage propose 2 options au client :
– Option Achat : prix d’achat de la voiture 22 400 €. Assurance obligatoire 75 € par mois.
– Option Location : 425 € par mois, assurance comprise.
L’objectif de cet exercice est de comparer ces deux options.
Partie A
1. Montrer qu’avec l’option Achat la dépense à la fin de la première année est de 23 300 €.
2. Après 36 mois, calculer l’économie réalisée par le client s’il choisit l’option Location ?
3. Afin de comparer les dépenses correspondantes à ces options le client a réalisé le tableau
suivant à l’aide d’un tableur :
| A | B | C | D | E | F | |
| 1 | Nombre de mois | 12 | 24 | 36 | 48 | 60 |
| 2 | Dépense en € Option Achat | 23300 | 24200 | 25100 | 26000 | 26900 |
| 3 | Dépense en € Option Location |
Quelle formule doit être saisie dans la cellule B3 qui, étendue jusqu’à la cellule F3, permet de compléter le tableau ?
Partie B
On souhaite maintenant modéliser les deux options précédentes par des fonctions.
On note \(x\) la durée écoulée en mois depuis la livraison de la voiture.
La fonction \(g\), permettant de calculer la dépense correspondant à l’option Location, peut s’écrire sous la forme : \(g(x)=425x\).
4. Déterminer l’expression de \(f(x)\) permettant de calculer la dépense correspondant à l’option Achat.
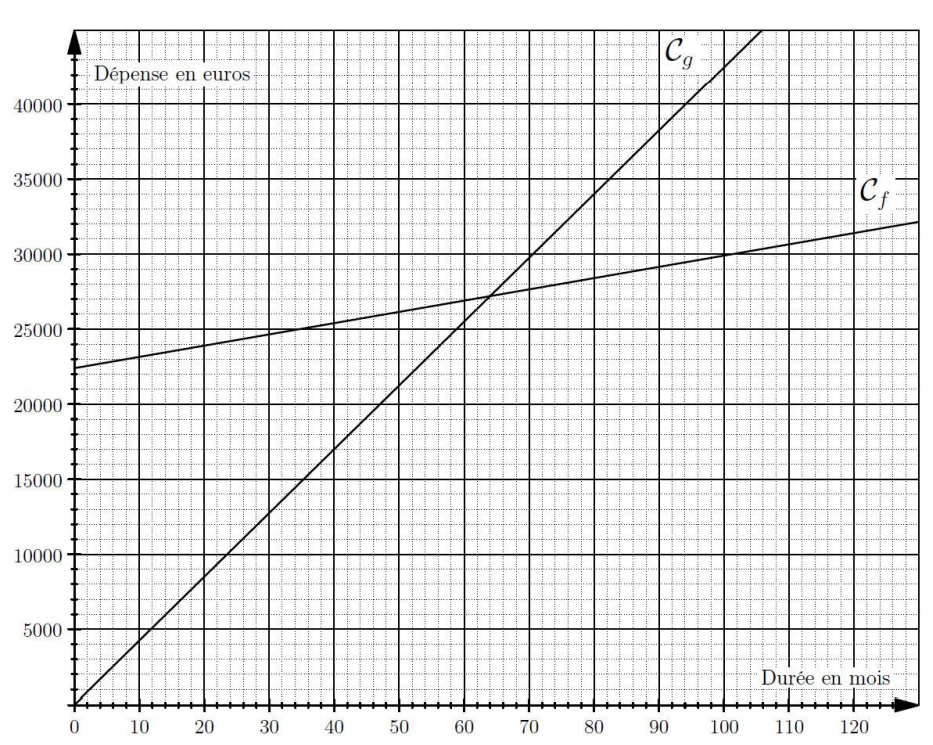
5. Sur le graphique ci-dessous, on a tracé les courbes représentatives \(\mathcal{C}_f\) et \(\mathcal{C}_g\) des fonctions \(f\) et \(g\).
Par lecture graphique, déterminer à partir de combien de mois, l’option Achat est la plus avantageuse.
Voir le corrigé détaillé : Corrigé du brevet de maths 2025 en France
Bien travailler avec brevet France 2025
Tout d’abord, fais l’exercice sans regarder la solution. Ensuite, vérifie chaque résultat avec soin. Ainsi, chaque erreur devient une occasion de progresser. Par ailleurs, en outre, quelques minutes par jour suffisent pour retenir l’essentiel.
Par exemple, refais un exercice raté deux jours plus tard. Enfin, le programme officiel de mathématiques est détaillé sur le site Éduscol. Également, tu peux continuer avec brevet de maths 2021 : sujet blanc n° 3 en PDF.
