DIPLÔME NATIONAL DU BREVET
BREVET BLANC 2024
MATHEMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 100 points.
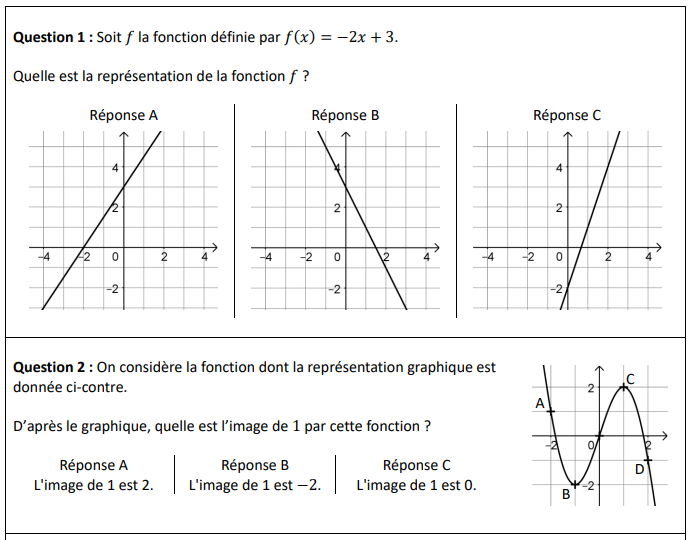
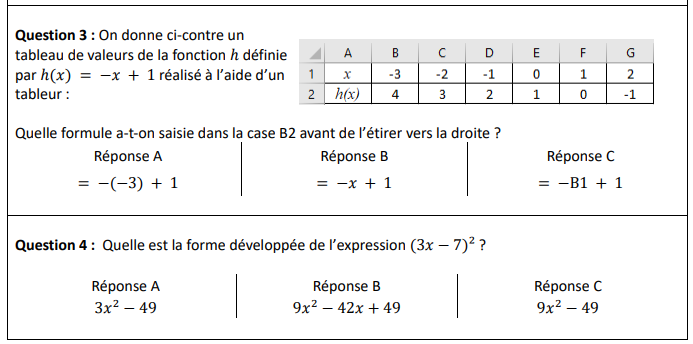
Exercice 1 (16 points)
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n’est ici demandée.
Pour chaque question, trois réponses sont proposées, une seule est exacte. Écrire sur votre copie le
numéro de la question et la réponse correspondante.
Exercice 2 (22 points)
Olivia a décidé d’installer, sur le sol plat de son jardin, quatre panneaux photovoltaïques pour produire
une partie de l’électricité qu’elle consomme.
Pour incliner ses panneaux et obtenir un fonctionnement optimal, Olivia choisit de fabriquer elle-même
un support.
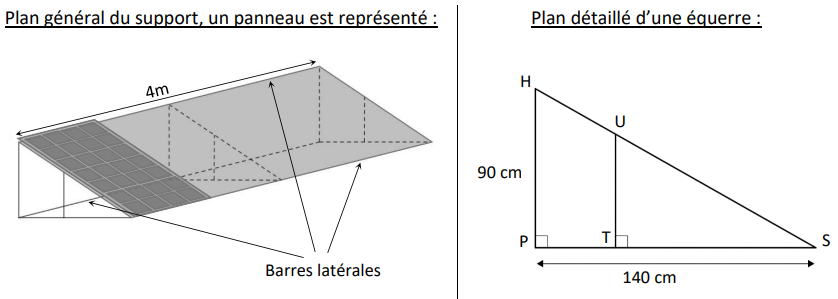
Pour cela, elle réalise les schémas suivants du support qui sera constitué de 3 équerres
identiques, reliées entre elles par 3 barres latérales de 4m de long.
Chaque support est prévu pour accueillir quatre panneaux.
1) a) Vérifier que la distance HS arrondie au millimètre est égale à 166,4 cm.
b) Pour que le panneau soit bien tenu, le fabricant conseille que la distance HS du support mesure
au moins 95% de la longueur du panneau. On rappelle que cette longueur mesure 1 700 mm.
Ce support sera-t-il conforme au conseil du fabricant ?
2) L’angle d’inclinaison 
permettra-t-il un fonctionnement optimal des panneaux ?
3) Pour consolider l’ensemble, Olivia fixe, à l’intérieur de ses équerres, une barre de renfort de 50 cm
de longueur. Sur le plan détaillé d’une équerre, cette barre est représentée par le segment [UT]
perpendiculaire au segment [PS].
Calculer la longueur ST. On arrondira au millimètre.
4) Olivia achète des tubes en acier inoxydable de longueur 4,5 m à 37 € l’unité pour fabriquer le
support composé des trois équerres et des trois barres latérales.
Montrer qu’elle doit prévoir un budget minimum de 222 € pour l’achat des tubes en acier inoxydable.
Exercice 3 (18 points)
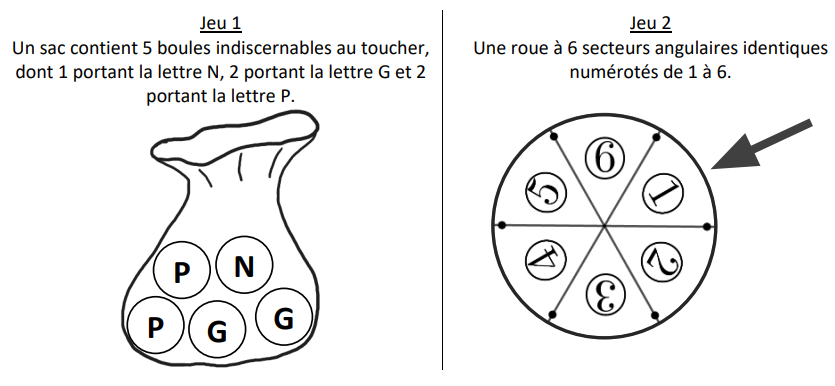
Dans cet exercice, on étudie la probabilité de gain des deux jeux ci-dessous.
Partie A :
1) On considère le jeu 1.
On pioche une boule au hasard dans ce sac et on note la lettre inscrite sur la boule choisie.
On considère qu’on a gagné si on pioche la lettre G.
Montrer que la probabilité de gagner avec ce jeu est de .
2) On considère le jeu 2.
On fait tourner la roue et on note le nombre inscrit sur le secteur pointé par la flèche.
On considère qu’on a gagné si on s’arrête sur un nombre premier.
Quelle est la probabilité de gagner à ce jeu ?
3) a) Quel est le jeu qui présente la plus faible probabilité de gagner ?
b) Proposer une liste de boules à rajouter pour que la probabilité de gagner avec le jeu 1 soit de .
Partie B :
Dans cette partie, toute trace de recherche sera valorisée.
On choisit finalement de combiner les deux jeux.
Dans un premier temps, le joueur doit tirer une boule dans le sac du jeu 1.
On doit ensuite faire tourner la roue du jeu 2.
Le joueur gagne un lot s’il a tiré une boule portant la lettre G et si la roue s’arrête sur un secteur angulaire
dont le numéro est un nombre premier.
Quelle est la probabilité de gagner à cette combinaison des deux jeux ?
Exercice 4 (22 points)
On considère le programme de calcul suivant :
- Choisir un nombre
- Prendre le carré de ce nombre
- Multiplier le résultat par 2
- Ajouter le nombre de départ
- Soustraire 66
1) a) Montrer que si le nombre choisi au départ est 4, le résultat obtenu est -30.
b) Quel résultat obtient-on si le nombre choisi au départ est -3 ?
2) a) On s’intéresse au bloc d’instruction ci-dessous intitulé « Programme de calcul ».
On souhaite le compléter pour calculer le résultat obtenu avec le programme de calcul en
fonction du nombre choisi au départ.
On précise que deux variables ont été créées : « nombre choisi » qui correspond au nombre
choisi au départ, et « Résultat ».
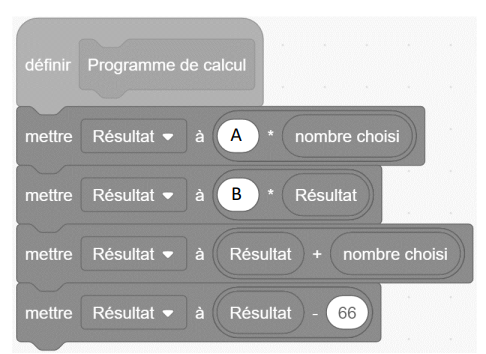
Écrire sur votre copie le contenu qui doit être inséré dans les emplacements A et B. Aucune
justification n’est attendue pour cette question.
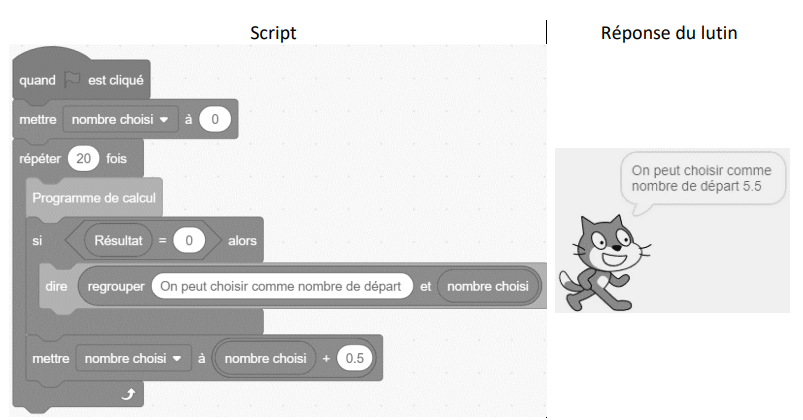
b) Lucie insère le bloc précédent dans le script ci-dessous et observe la réponse donnée par le
lutin :
À quoi correspond la valeur 5,5 donnée comme réponse par le lutin avec le programme de
Lucie ?
3) On nomme le nombre choisi au départ.
a) Déterminer l’expression obtenue par ce programme de calcul en fonction de .
b) On admet que est la forme factorisée de l’expression trouvée à la question
précédente.
Pour quelle(s) valeur(s) de , le résultat obtenu avec le programme est-il égal à 0 ?
Exercice 5 (22 points)
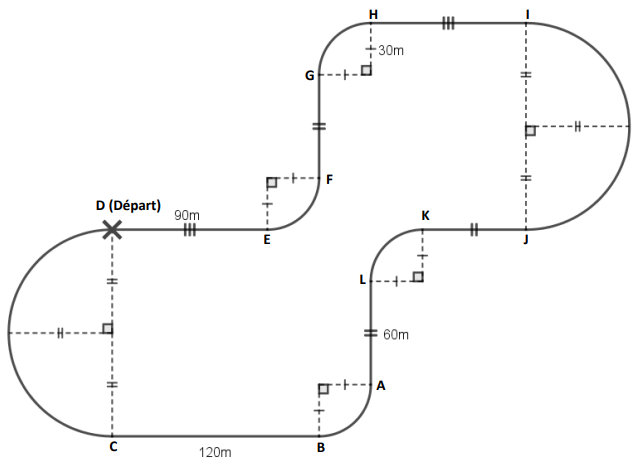
Un professionnel et un amateur vont faire une séance de karting sur la piste ci-dessous (représentée en
traits pleins).
Cette piste est constituée de segments, de demi-cercles et de quarts de cercles.
Le professionnel fait un tour de piste en 60 secondes.
L’amateur fait un tour de piste en 72 secondes.
1) Montrer que la longueur de la piste est de 1 045 m, arrondie à l’unité près.
Toute trace de recherche sera valorisée.
2) Calculer la vitesse moyenne du professionnel en m/s. On arrondira au centième près.
3) Pour des raisons de sécurité sur ce circuit, les amateurs ne doivent pas dépasser les 60 km/h de
moyenne. Cet amateur respecte-t-il les règles de sécurité ?
4) Le professionnel et l’amateur partent en même temps de la ligne de départ et font plusieurs
tours de circuit. On rappelle que le professionnel effectue un tour en 60 s et l’amateur en 72 s.
a) Décomposer 60 et 72 en produit de facteurs premiers.
b) Au bout de combien de temps se retrouveront-ils pour la première fois sur la ligne de
départ ensemble ?
c) Combien auront-ils alors effectué de tours chacun ?
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2024 blanc n° 1 : sujet et corrigé en PDF.» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
