Brevet de maths 2019 en Grèce à télécharger en PDF
Brevet des collèges Grèce
Le 18 juin 2019
EXERCICE 1 : 12 POINTS
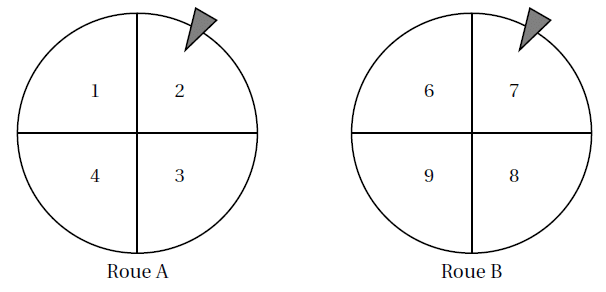
Mathilde fait tourner deux roues de loterie A et B comportant chacune quatre secteurs numérotés
comme sur le schéma ci-dessous :
La probabilité d’obtenir chacun des secteurs d’une roue est la même. Les flèches indiquent les deux
secteurs obtenus.
L’expérience de Mathilde est la suivante : elle fait tourner les deux roues pour obtenir un nombre à
deux chiffres. Le chiffre obtenu avec la roue A est le chiffre des dizaines et celui avec la roue B est le
chiffre des unités.
Dans l’exemple ci-dessus, elle obtient le nombre 27 (Roue A : 2 et Roue B : 7).
1. Écrire tous les nombres possibles issus de cette expérience.
2. Prouver que la probabilité d’obtenir un nombre supérieur à 40 est 0,25.
3. Quelle est la probabilité que Mathilde obtienne un nombre divisible par 3?
EXERCICE 2 : 20 POINTS
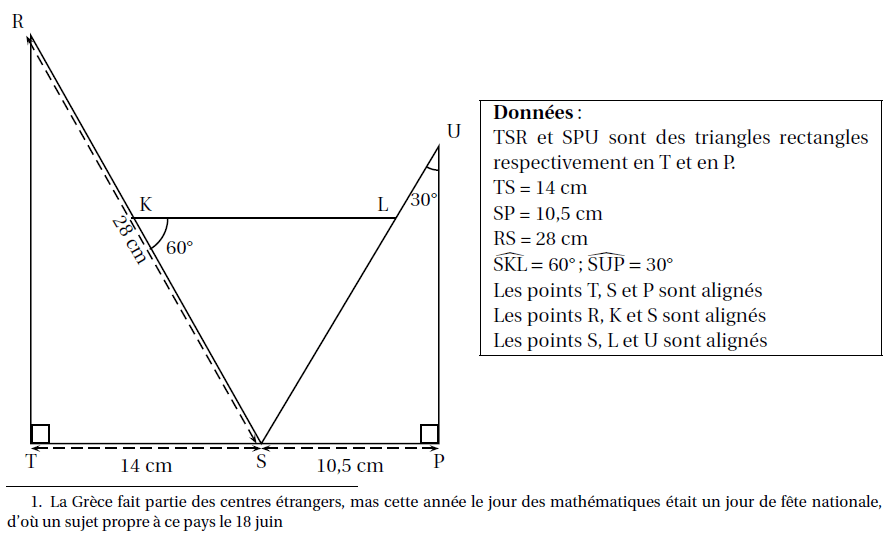
1. Montrer que la mesure de l’angle TSR est 60°.
2. Démontrer que les triangles SRT et SUP sont semblables
3. Déterminer le coefficient de réduction liant les triangles SRT et SUP.
4. Calculer la longueur SU.
5. Quelle est la nature du triangle SKL? A justifier.
EXERCICE 3 : 15 POINTS
Marc et Jim, deux amateurs de course à pied, s’entraînent sur une piste d’athlétisme dont la longueur
du tour mesure 400 m.
Marc fait un temps moyen de 2 minutes par tour.
Marc commence son entrainement par un échauffement d’une longueur d’un kilomètre.
1. Combien de temps durera l’échauffement de Marc?
2. Quelle est la vitesse moyenne de course de Marc en km/h?
À la fin de l’échauffement, Marc et Jim décident de commencer leur course au même point de départ
A et vont effectuer un certain nombre de tours.
Jim a un temps moyen de 1 minute et 40 secondes par tour.
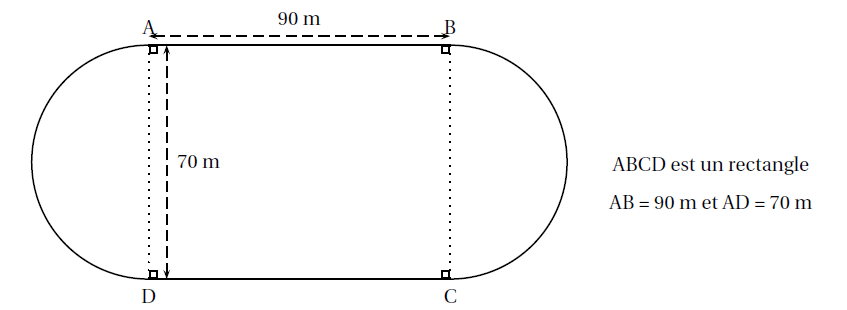
Le schéma ci-dessous représente la piste d’athlétisme de Marc et Jim constituée de deux segments
[AB] et [CD] et de deux demi-cercles de diamètre [AD] et [BC).
(Le schéma n’est pas à l’échelle et les longueurs indiquées sont arrondies à l’unité.)
3. Calculer le temps qu’il faudra pour qu’ils se retrouvent ensemble, au même moment, et pour
la première fois au point A.
Puis déterminer combien de tours de piste cela représentera pour chacun d’entre eux.
Toute trace de recherche, même non aboutie, devra apparaître sur la copie. Elle sera prise en
compte dans l’évaluation.
EXERCICE 4 : 16 POINTS
Pour occuper son petit frère, Lucie, qui aime bien l’informatique, décide de fabriquer des rosaces à
colorier. Elle décide de partir d’un motif ayant la forme d’un losange.
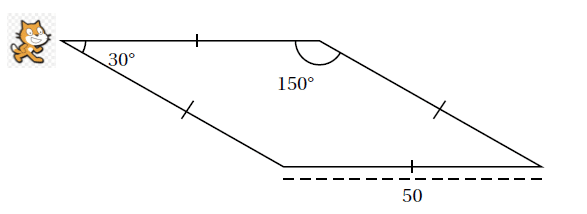
A l’aide d’un logiciel de programmation assisté (type scratch), elle a représenté le motif suivant :
Il s’agit d’un losange dont les côtés ont pour longueur 50 pixels et dont les angles aigus mesurent
30°et les angles obtus 150°.
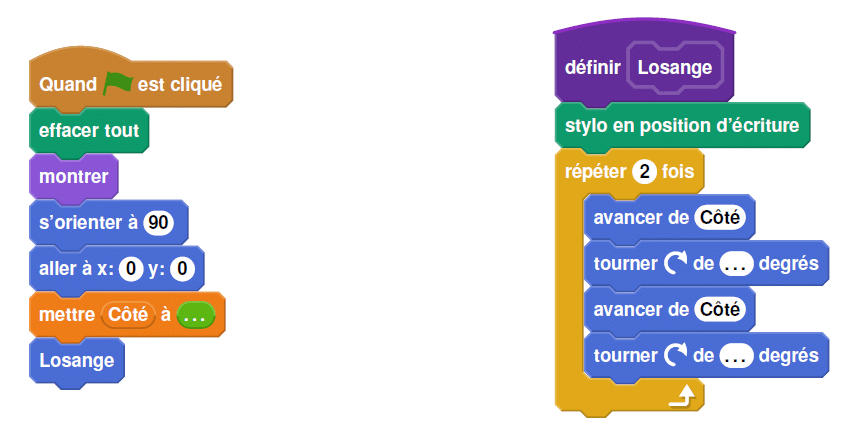
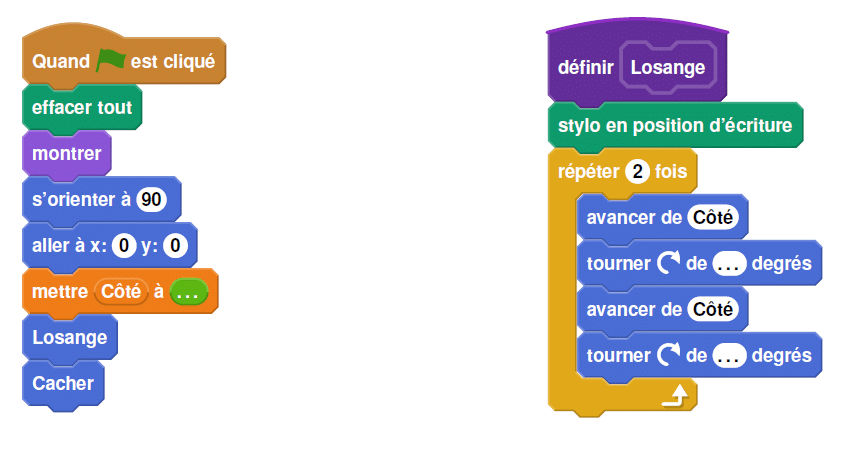
Afin de représenter ce losange, elle a écrit le programme suivant :
1. Compléter ci-dessous, le programme ci-dessus en remplaçant les pointillés par les
bonnes valeurs pour que le losange soit dessiné tel qu’il est défini.
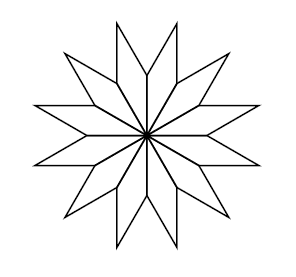
2. En utilisant le losange ci-dessus, elle obtient la rosace suivante qui n’est pas en vraie grandeur :
Quelle transformation géométrique, partant du premier losange ABCD et répétée 12 fois, a été
utilisée pour obtenir cette figure? Définir le mieux que vous pouvez cette transformation.
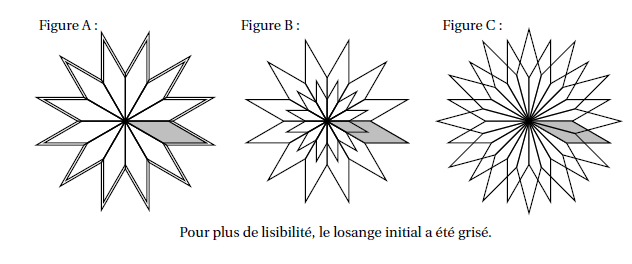
3. Pour finir, Lucie souhaite encore compléter cette rosace de trois façons différentes. Pour cela trois programmes ont été effectués.
Recopier sur votre copie le numéro des trois programmes, et pour chacun, la lettre de la figure qui lui est associée.
EXERCICE 5 : 15 POINTS
On donne le programme de calcul suivant :
1. Montrer que lorsqu’on choisit le nombre 2 au départ, on obtient le nombre 5 au final.
2. Quel résultat obtient-on lorsqu’on choisit au départ le nombre −3?
3. On définit une fonction f qui, à tout nombre x choisi à l’entrée du programme, associe le résultat
obtenu à la fin de ce programme.
Ainsi, pour tout x,on obtient f (x) = (x +1)² −x²
Montrer que f (x) = 2x +1.
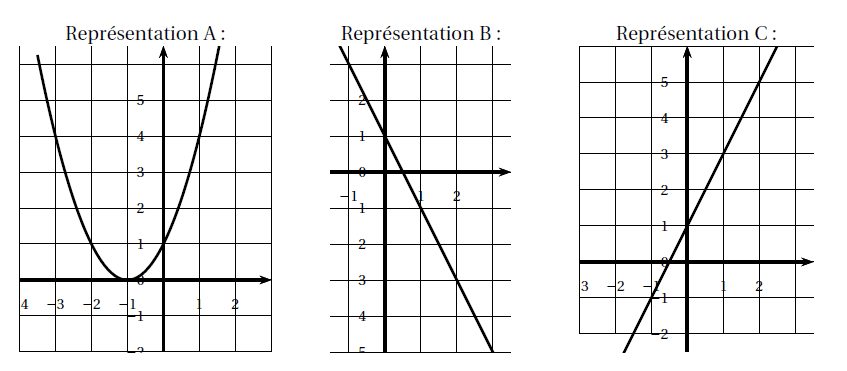
4. Cette question est un questionnaire à choix multiples (QCM).
Dans chaque cas, une seule réponse est correcte. Pour chacune des questions, écrire sur la
copie le numéro de la question et la bonne réponse.
Aucune justification n’est demandée.
EXERCICE 6 : 22 POINTS
Dans le village de Jean, une brocante est organisée chaque année lors du premier week-end de juillet.
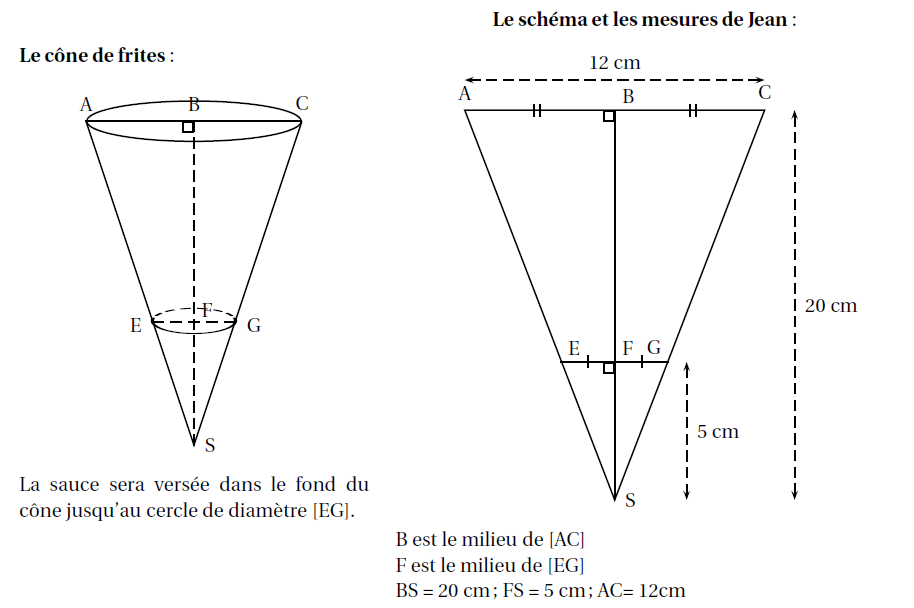
Jean s’est engagé à s’occuper du stand de vente de frites. Pour cela, il fabrique des cônes en papier
qui lui serviront de barquette pour les vendre.
Dans le fond de chaque cône, Jean versera de la sauce : soit de la mayonnaise, soit de la sauce tomate.
Il décide de fabriquer 400 cônes en papier et il doit estimer le nombre de bouteilles de mayonnaise et de sauce tomate à acheter pour ne pas en manquer.
Voici les informations dont Jean dispose pour faire ses calculs :
Les acheteurs :
80% des acheteurs prennent de la sauce tomate et tous les autres prennent de la mayonnaise.
Les sauces :
La bouteille de mayonnaise est assimilée à un cylindre de révolution dont le diamètre de base est
5 cm et la hauteur est 15 cm.
La bouteille de sauce tomate a une capacité de 500 mL.
1. Montrer que le rayon [EF] du cône de sauce a pour mesure 1,5 cm.
2. Montrer que le volume de sauce pour un cône de frites est d’environ 11,78 cm3
3. Déterminer le nombre de bouteilles de chaque sauce que Jean devra acheter.
Toute trace de recherche même non aboutie devra apparaître sur la copie.

Retrouvez chaque semaine de nouveaux cours de maths adaptés à votre niveau!
Continuez à vous exercer en consultant les exercices de mathématiques 3 ème .
Vous pouvez également retrouver de nombreuses vidéos de maths sur notre chaine Youtube!
Les mathématiques avec nous c’est facile, alors comptez sur nous !
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2019 en Grèce à télécharger en PDF» au format PDF.
D'autres cours et exercices à consulter
- Polynésie Française : brevet de maths 2022 avec sujet et corrigé
- Brevet de maths 2024 aux centres étrangers avec sujet et corrigé.
- Asie et Pacifique : brevet de maths 2022 avec sujet et corrigé
- Brevet Maths 2021 : sujet et corrigé du brevet blanc de maths
- Brevet Maths 2021 : sujet corrigé blanc pour la révision du DNB
- Brevet Maths 2021 : sujet blanc pour réviser le brevet
- Brevet de maths 2022 aux centres étrangers : sujet et corrigé du brevet.
- Brevet de maths 2017 : sujet blanc