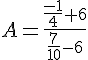Brevet de maths

Sujet du brevet de maths 2017 blanc où les exercices sont indépendants les uns des autres. Sauf indication contraire, toutes les réponses doivent être justifiées et les calculs doivent être détaillés. Le matériel de géométrie classique est autorisé.

EPREUVE DE MATHEMATIQUES de type BREVET
Durée : 2 heures
L’usage de la calculatrice est autorisé.
L’usage du dictionnaire n’est pas autorisé.

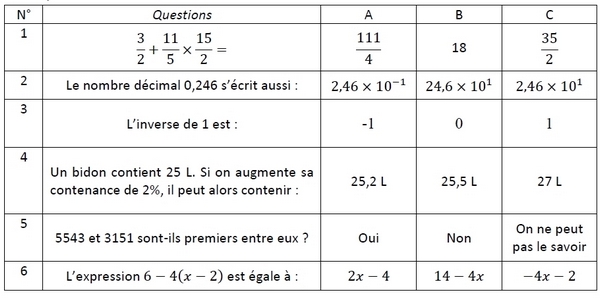
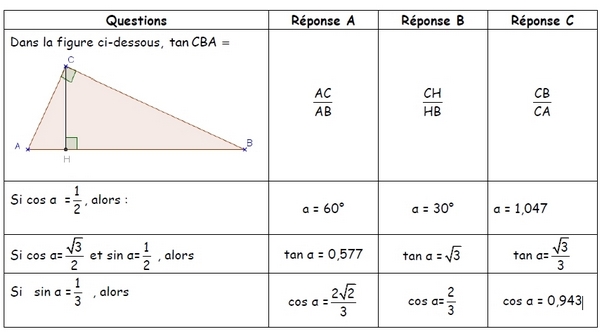
Exercice 1 : (4 points)

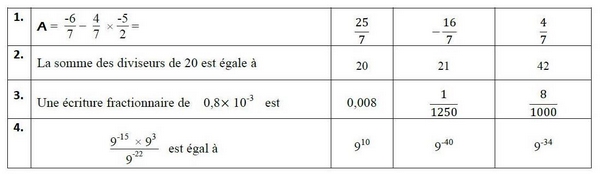
Dans ce questionnaire à choix multiple, pour chaque question, trois réponses sont proposées, et une seule est exacte. Pour chaque question indiquer sur la copie le numéro de la question et recopier la bonne réponse. Aucune justification n’est attendue.

Exercice 2 : (3 points)

Les questions 1) et 2) sont indépendantes.

1) a) Calculer en détaillant les étapes du calcul.

b) A est-il un nombre décimal ? Justifier.

2) Pour son herbier, Héloïse collectionne des feuilles jaunes, vertes et rouges :

Elle a de feuilles vertes et de feuilles rouges.

A quelle fraction de la collection correspondent les feuilles jaunes ?

Exercice 3 : (2 points)

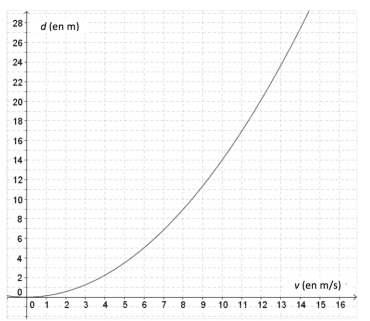
Le 14 octobre 2012, Félix Baumgartner, a effectué un saut d’une altitude de 38 969,3mètres. La première partie de son saut s’est faite en chute libre (parachute fermé).

La seconde partie, s’est faite avec un parachute ouvert. Son objectif était d’être le premier homme à « dépasser le mur du son ». « dépasser le mur du son » signifie atteindre une vitesse supérieure ou égale à la vitesse du son, c’est à dire .

La Fédération Aéronautique Internationale a établi qu’il avait atteint la vitesse maximale de  au cours de sa chute libre.

A-t-il atteint son objectif ? Justifier votre réponse.

Exercice 4: (4 points)

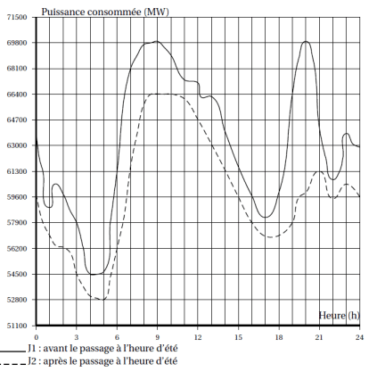
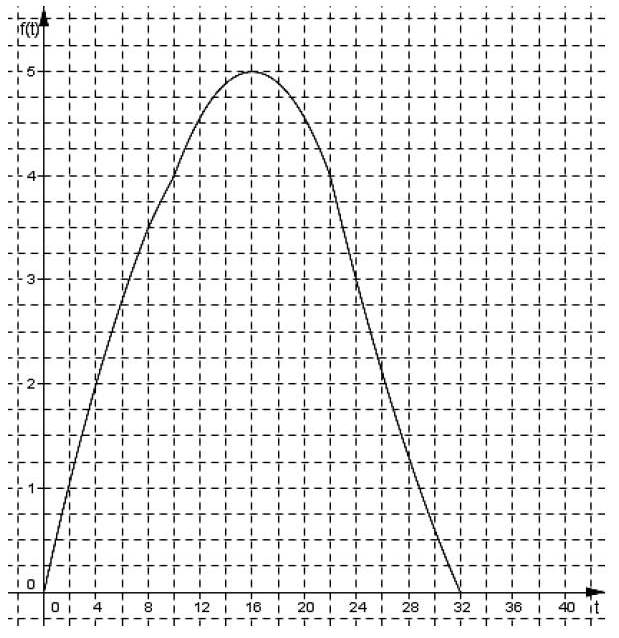
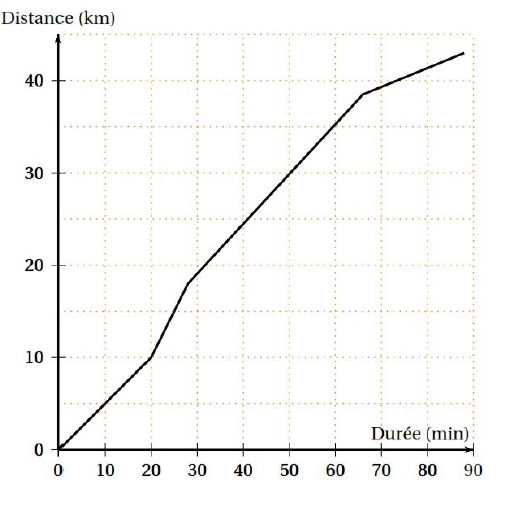
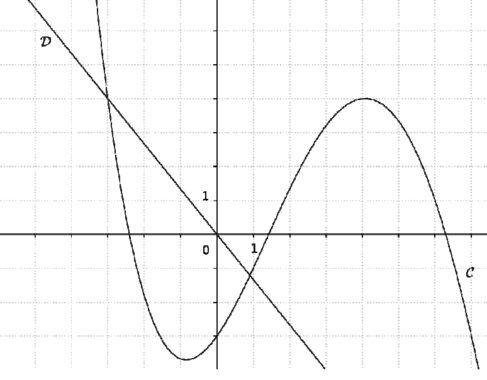
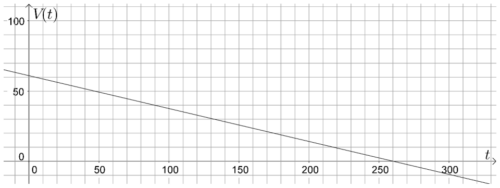
L’objectif du passage à l’heure d’été est de faire correspondre au mieux les heures d’activité avec les heures d’ensoleillement pour limiter l’utilisation de l’éclairage artificiel. Le graphique ci-dessous représente la puissance consommée en mégawatts (MW), en fonction des heures (h) de deux journées J1 et J2, J1 avant le passage à l’heure d’été et J2 après le passage à l’heure d’été.

Par lecture graphique, répondre aux questions posées.

On arrondira, si nécessaire, les résultats à la demi-heure.

1) Pour la journée J1, quelle est la puissance consommée à 7 h ?

2) Pour la journée J2, à quelle(s) heure(s) de la journée a-t-on une puissance consommée de 54 500 MW?

3) À quel moment de la journée le passage à l’heure d’été permet-il le plus d’économies ?

4) Quelle puissance consommée a-t-on économisée à 19 h30 ?

Exercice 5: (4 points)

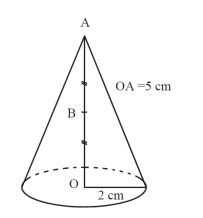
On considère un cône de révolution de hauteur [AO] mesurant 5 cm et dont la base a pour rayon 2 cm. Le point A est le sommet du cône et O est le centre de sa base.

1) Calculer le volume du cône en .

Donner la valeur exacte puis arrondir à l’unité.

Rappel : Volume d’un cône de révolution

où h désigne la hauteur et r le rayon du cône de révolution.

2) On effectue une réduction de ce cône de facteur   . On obtient un nouveau cône de sommet A dont la base a pour centre B, milieu de [AO].

Est-il vrai que le volume du petit cône est égal à la moitié du volume du cône initial ? Justifier.

Exercice 6: (4 points)

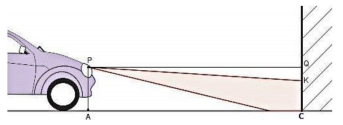
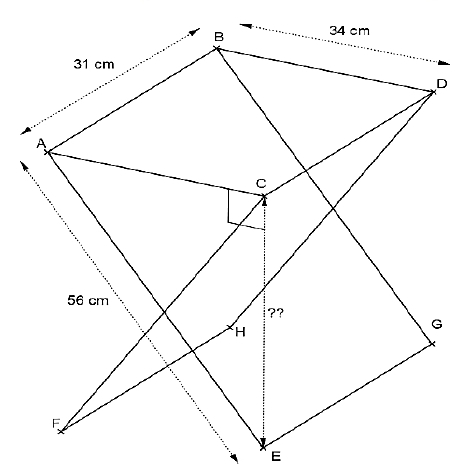
Pour construire un mur vertical, il faut parfois utiliser un coffrage et un étayage qui maintiendront la structure verticale, le temps que le béton sèche (figure 1).

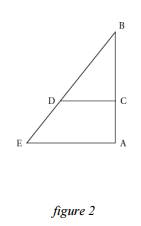
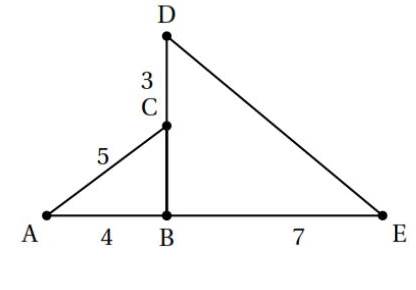
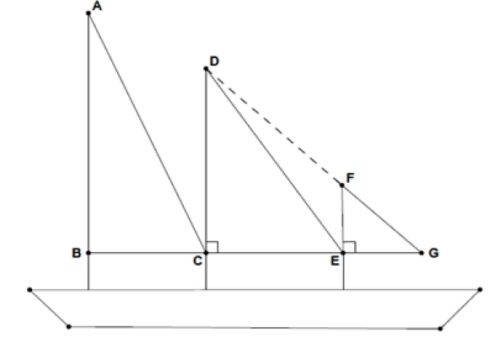
Cet étayage peut se représenter par le schéma ci-dessus (figure 2). Les poutres de fer sont coupées et fixées de façon que :

•  Les segments [AB] et [AE] sont perpendiculaires;
•  C est situé sur la barre [AB] ; D est situé sur la barre [BE] ;
•  AB = 3,5m; AE = 2,625m et CD = 1,5m.

1) Calculer BE.

2) On admet, de plus, que (CD) et (AB) sont perpendiculaires.

A quelle distance de B est situé le point C?

Exercice 7 : (3 points)

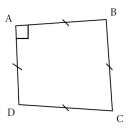
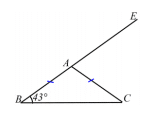
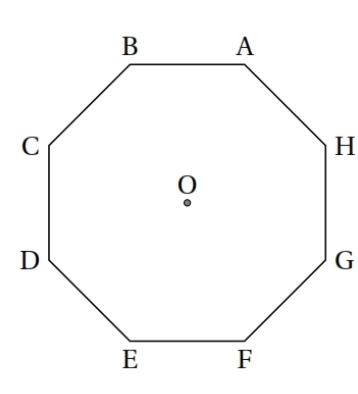
Attention les figures tracées ne respectent ni les mesures de longueur, ni les mesures d’angle. Répondre par « vrai » ou « faux » ou « on ne peut pas savoir » à chacune des affirmations suivantes et expliquer votre choix.

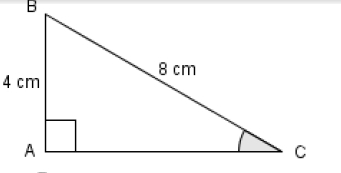
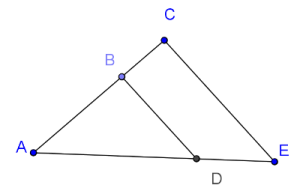
1) « Tout triangle inscrit dans un cercle est rectangle. »

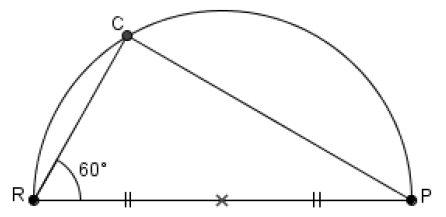
2) « Si un point M appartient à la médiatrice d’un segment [AB] alors le triangle AMB est isocèle. »

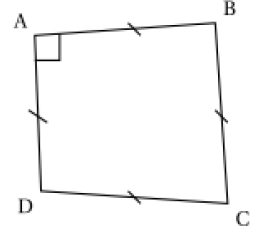
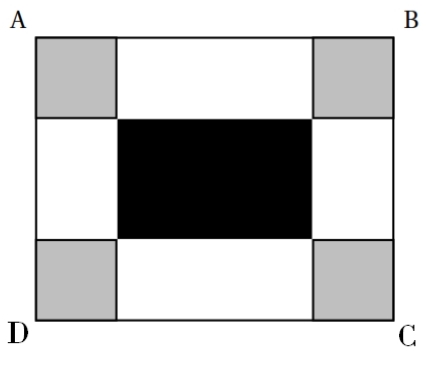
3) « Le quadrilatère ABCD ci-contre est un carré. »

Exercice 8 : (4 points)

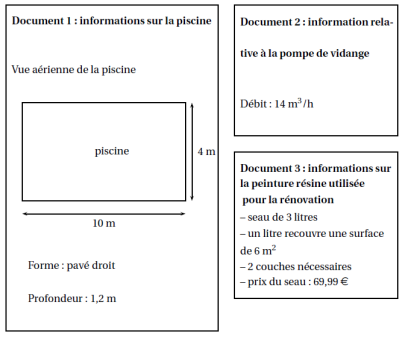
Voici les caractéristiques d’une piscine qui doit être rénovée :

1) Le propriétaire commence par vider la piscine avec la pompe de vidange.

Cette piscine est remplie à ras bord. Sera-t-elle vide en moins de 4 heures ?

2) Il repeint ensuite toute la surface intérieure de cette piscine avec de la peinture résine.

Quel est le coût de la rénovation?

Exercice 9 : (3 points)

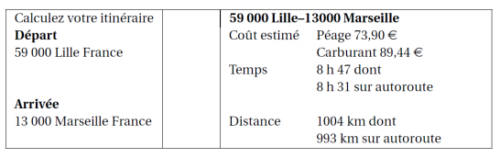
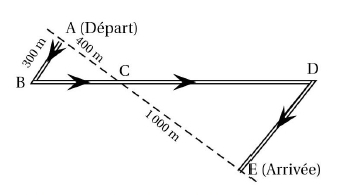
Pour préparer son voyage à Marseille, Julien utilise un site Internet pour choisir le meilleur itinéraire. Voici le résultat de sa recherche :

1) Sachant que la sécurité routière préconise au moins une pause de 10 à 20minutes toutes les deux heures de conduite, quelle doit être la durée minimale que Julien doit prévoir pour son voyage ?

2) Pour cette question, faire apparaître sur la copie la démarche utilisée. Toute trace de recherche sera prise en compte lors de l’évaluation même si le travail n’est pas complètement abouti.

Sachant que le réservoir de sa voiture a une capacité de 60 L et qu’un litre d’essence coûte 1,42€ , peut-il faire le trajet avec un seul plein d’essence en se fiant aux données du site internet ?

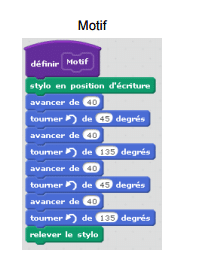
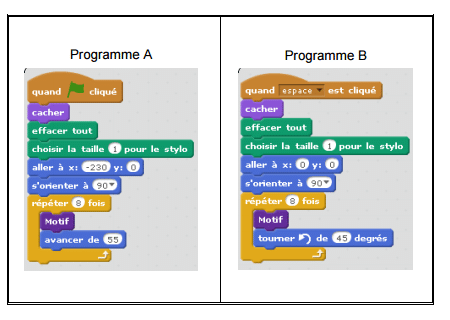
Exercice 10 : (5 points)

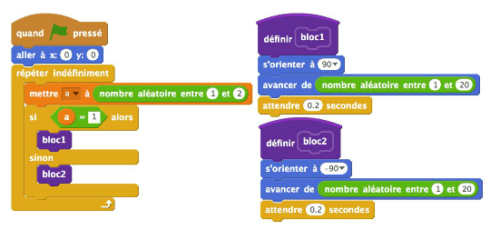
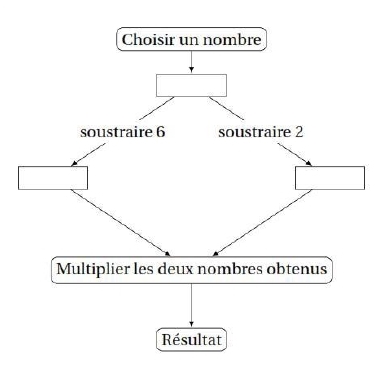
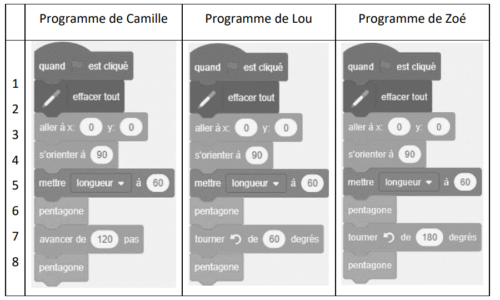
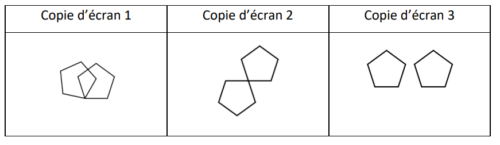
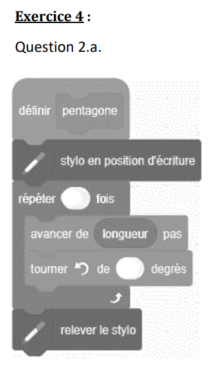
Que fait ce lutin quand le programme est exécuté ?

Ce sujet du brevet de maths 2017 a été rédigé par une équipe de l’éducation nationale.

 Consulter le corrigé en ligne

Nouveau sujet de la nouvelle épreuve de mathématiques pour la session 2017 suite à la réforme du collège.

Ce sujet officiel est tiré du site Eduscol.

Exercice 1
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant soigneusement la réponse.
1) Un sac contient 6 jetons rouges, 2 jetons jaunes et des jetons verts.
La probabilité de tirer un jeton vert vaut 0,5.
Affirmation : le sac contient 4 jetons verts.
2) En informatique, on utilise comme unités de mesure les multiples suivants de l’octet :
,  ,  , ,
où Ko est l’abréviation de kilooctet, Mo celle de mégaoctet, Go celle de gigaoctet, To celle de téraoctet.
On partage un disque dur de 1,5 To en dossiers de 60 Go chacun.
Affirmation : on obtient ainsi 25 dossiers.

3) Sur la figure codée ci-dessous, les points B, A et E sont alignés.
Affirmation : l’angle  mesure 137°.

4) Un verre de forme conique est complètement rempli.
On verse son contenu de sorte que la hauteur du liquide soit divisée par 2.
Affirmation : le volume du liquide est divisé par 6.

Exercice 2
Le marnage désigne la différence de hauteur entre la basse mer et la pleine mer qui suit.
On considère qu’à partir du moment où la mer est basse, celle-ci monte de 1/12 du marnage pendant la première heure, de 2/12 pendant la deuxième heure, de 3/12 pendant la troisième heure, de 3/12 pendant la quatrième heure, de 2/12 pendant la cinquième heure et de 1/12 pendant la sixième heure. Au cours de chacune de ces heures, la montée de la mer est supposée régulière.
1) À quel moment la montée de la mer atteint-elle le quart du marnage ?
2) À quel moment la montée de la mer atteint-elle le tiers du marnage ?

Exercice 3
Pour la fête d’un village on organise une course cycliste. Une prime totale de 320 euros sera répartie entre les trois premiers coureurs.
Le premier touchera 70 euros de plus que le deuxième et le troisième touchera 80 euros de moins que le deuxième.
Déterminer la prime de chacun des trois premiers coureurs.

Exercice 4

1) Pour réaliser la figure ci-dessus, on a défini un motif en forme de losange et on a utilisé l’un des deux programmes A et B ci-dessous.

Déterminer lequel et indiquer par une figure à main levée le résultat que l’on obtiendrait avec l’autre programme.

2) Combien mesure l’espace entre deux motifs successifs ?

3) On souhaite réaliser la figure ci-dessous :

Pour ce faire, on envisage d’insérer l’instruction dans le programme utilisé à la question 1.

Où faut-il insérer cette instruction ?

Exercice 5
Pour régler les feux de croisement d’une automobile, on la place face à un mur vertical. Le phare, identifié au point P, émet un faisceau lumineux dirigé vers le sol.
On relève les mesures suivantes :
PA = 0,7 m, AC = QP = 5 m et CK = 0,61 m.
Sur le schéma ci-contre, qui n’est pas à l’échelle, le point S représente l’endroit où
le rayon supérieur du faisceau rencontrerait le sol en l’absence du mur.
On considère que les feux de croisement sont bien réglés si le rapport  est compris entre 0,015 et 0,02.
1) Vérifier que les feux de croisement de la voiture sont bien réglés.
2) À quelle distance maximale de la voiture un obstacle se trouvant sur la route est-il éclairé par les feux de croisement ?

Exercice 6
Un panneau mural a pour dimensions 240 cm et 360 cm. On souhaite le recouvrir avec des carreaux de forme carrée, tous de même taille, posés bord à bord sans jointure.
1) Peut-on utiliser des carreaux de : 10 cm de côté ? 14 cm de côté ? 18 cm de côté ?
2) Quelles sont toutes les tailles possibles de carreaux comprises entre 10 et 20 cm ?
3) On choisit des carreaux de 15 cm de côté. On pose une rangée de carreaux bleus sur le pourtour et des carreaux blancs ailleurs.

Combien de carreaux bleus va-t-on utiliser ?

Exercice 7
La distance de freinage d’un véhicule est la distance parcourue par celui-ci entre le moment où le conducteur commence à freiner et celui où le véhicule s’arrête. Celle-ci dépend de la vitesse du véhicule. La courbe ci-dessous donne la distance de freinage d, exprimée en mètres, en fonction de la vitesse v du véhicule, en m/s,sur une route mouillée.

1) Démontrer que 10 m/s = 36 km/h.
2) a. D’après ce graphique, la distance de freinage est-elle proportionnelle à la vitesse du véhicule ?
b. Estimer la distance de freinage d’une voiture roulant à la vitesse de 36 km/h.
c. Un conducteur, apercevant un obstacle, décide de freiner. On constate qu’il a parcouru 25 mètres entre le moment où il commence à freiner et celui où il s’arrête. Déterminer, avec la précision permise par le graphique, la vitesse à laquelle il roulait en m/s.
3) On admet que la distance de freinage d, en mètres, et la vitesse v, en m/s, sont liées par la relation .
a. Retrouver par le calcul le résultat obtenu à la question 2b.
b. Un conducteur, apercevant un obstacle, freine ; il lui faut 35 mètres pour s’arrêter.

À quelle vitesse roulait-il ?
 Consulter le corrigé en ligne

Un sujet du brevet blanc de maths 2023 afin de réviser en ligne sur Mathovore et de se préparer pour les épreuves du brevet des collèges en juin 2023.

Brevet blanc de maths 2023

L’orthographe, le soin, la qualité et la précision de la rédaction seront pris en compte à hauteur de 4 points sur 40 dans l’évaluation de la copie. L’utilisation de la calculatrice est autorisée.
Aucun prêt de matériel n’est autorisé. Conserver le sujet pour correction.

Exercice 1 : ( 4 points )

Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n’est demandée.
Pour chacune des questions, trois réponses sont proposées ; une seule est exacte.
Chaque bonne réponse donne un point, une réponse fausse ou une absence de réponse n’enlève aucun point.
Pour chacune des quatre questions, indiquer sur la copie le numéro de la question et recopier la réponse exacte.

Exercice 2 : ( 4,5 points )

Voici une feuille de calcul obtenue à l’aide d’un tableur ; dans cet exercice on cherche à comprendre comment cette feuille a été remplie.

1. En observant les valeurs du tableau, proposer une formule à entrer dans la cellule C1, puis à recopier vers le bas.
2. Dans cette question, on laissera sur la copie toutes les traces de recherche : elles seront valorisées. Le tableur fournit deux fonctions MAX et MIN. À partir de deux nombres, MAX renvoie la valeur la plus grande et MIN la plus petite. (exemple : MAX(23 ;12) = 23) Quelle formule a été entrée dans la cellule A2, puis recopiée vers le bas ?
3. Que représente le nombre figurant dans la cellule C5, par rapport aux nombres 216 et 126 ?
4. La fraction 216/126 est-elle irréductible ? Si ce n’est pas le cas, la rendre irréductible en détaillant les calculs.

Exercice 3 : ( 4,5 points )

Le parcours de cyclisme est une boucle de 10 km. Le point de départ est donc aussi le point d’arrivée.
À mi-parcours, les athlètes ont droit à un ravitaillement.
Le graphique ci-dessous représente la distance f(t) exprimée en kilomètres séparant Hélène du point d’arrivée en fonction du temps t exprimé en minutes.
On appelle f la fonction ainsi représentée.
Toutes les réponses seront données à l’aide du graphique.

1) Combien de kilomètres reste-t-il à parcourir au bout de 24 minutes ?
2) Déterminer l’image du nombre 4 par la fonction f.
3) Déterminer f(8).
4) Déterminer le ou les antécédent(s) du nombre 0 par la fonction f.
5) Pour quelle(s) valeur(s) de t a-t-on f(t) = 4 ?

Exercice 4 : ( 3 points )

Il existe différentes unités de mesure de température : en France on utilise le degré Celsius (°C), aux États-Unis on utilise le degré Fahrenheit (°F).
Pour passer des degrés Celsius aux degrés Fahrenheit, on multiplie le nombre de départ par 1,8 et on ajoute 32 au résultat.
1°) Qu’indiquerait un thermomètre gradué en degrés Fahrenheit si on le plonge dans une casserole d’eau qui gèle ? On rappelle que l’eau gèle à 0°C.
2°) Qu’indiquerait un thermomètre en degrés Fahrenheit si on le plonge dans une casserole d’eau à 23°C ?
3°) Si on appelle x la température en degrés Celsius et f(x) la température en degrés fahrenheit, exprimer f(x) en fonction de x.

Exercice 5 : ( 3 points )

Pour une bonne partie de pêche au bord d’un canal, il faut un siège pliant adapté ‼
Nicolas est de taille moyenne et pour être bien assis, il est nécessaire que la hauteur de l’assise du siège soit comprise entre 44 cm et 46 cm.
L’angle   est droit et ABDC est un rectangle.
La hauteur de ce siège lui est-elle adaptée ?

Exercice 6 : ( 5 points )

Un fût de déchets radioactifs (représenté ci-contre) a la forme d’un cylindre de rayon 0,6 mètre et de hauteur 1,5 mètre.

a) Calculer le volume d’un seul fût. On donnera la valeur exacte et la valeur arrondie au dm3 près.
b) On veut stocker ces fûts au contenu dangereux dans des bassins de stockage souterrains de forme parallélépipédique (voir photo).
Si l’on dispose d’un bassin de longueur 360 mètres, de largeur 150 m et de hauteur 9 mètres,
montrer que l’on peut alors y stocker 225 000 fûts.

c) Quel est le pourcentage d’espace perdu dans le bassin de stockage ?
Le résultat sera arrondi au dixième.

Exercice 7 : ( 4 points )

Attention les figures tracées ne respectent ni les mesures de longueur, ni les mesures d’angles.
Répondre par « vrai » ou « faux » ou « on ne peut pas savoir » à chacune des affirmations suivantes et expliquer votre choix.
1. Tout triangle inscrit dans un cercle est rectangle.
2. Si un point M appartient à la médiatrice d’un segment [AB], alors le triangle AMB est isocèle.
3. Dans le triangle ABC suivant :  .

4. Le quadrilatère ABCD ci-dessous est un carré.

Exercice 8 : ( 4 points )

Voici une carte découverte par Marco qui lui permettra de déterrer le fabuleux trésor de Batmath le pirate.
Les indications sont : R est le rocher en forme de crâne ; C le cocotier sous lequel est enterré le trésor ; P est le phare ; C est situé sur le demi-cercle de diamètre [PR].

On donne PR = 3000 brasses (ancienne unité de mesure de longueur correspondant à l’envergure des bras)

a) Démontrer que le triangle PRC est un triangle rectangle.
b) Calculer la distance RC en brasses.

Exercice 9  : exercice à prise d’initiative.

Michel possède 108 billes blanches et 135 billes noires qu’il veut vendre à la brocante près de chez lui. Pour cela, il veut préparer le plus grand nombre possible de sachets identiques (même nombre de billes blanches et même nombre de billes noires dans chaque sachet) en utilisant toutes ses billes.
Combien pèse un sachet de billes ?
Combien Michel pourra – t – il gagner au maximum en vendant ses sachets ?

Laisser une trace écrite de vos recherches, même incomplètes.
Elles seront prises en compte dans la notation.

 Consulter le corrigé en ligne