Brevet de maths 2022 aux centres étrangers : sujet et corrigé.

DIPLÔME NATIONAL DU BREVET

SESSION 2022

CENTRES ETRANGERS

MATHEMATIQUES
Série générale
Durée de l’épreuve : 2 h

Exercice 1 : 19 points.
Les deux parties de cet exercice sont indépendantes.
Partie A :
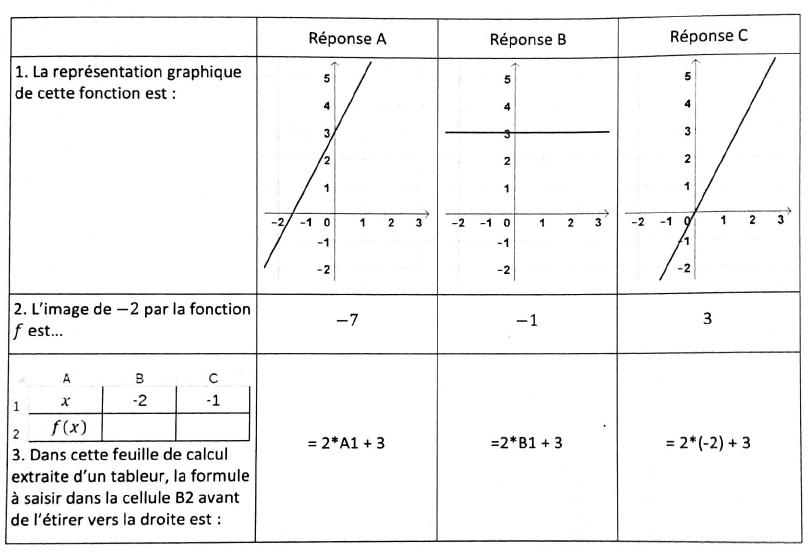
Cette partie est un questionnaire à choix multiples (QCM). Pour chaque question, trois réponses sont proposées, une seule est exacte.

Recopier le numéro de la question et indiquer, sans justifier dans cette partie seulement, la réponse choisie.
Dans toute cette partie, on considère la fonction définie par f(x) = 2x + 3.

Partie B :
1. Montrer que : $(2x-\,1)\,(3x\,+\,4)\,-2x\,=\,6x^2\,+\,3x\,-\,4$ .
2. On considère le triangle CDE tel que : CD = 3,6 cm ; CE =4,2 cm et DE = 5,5 cm.

Le triangle CDE est-il rectangle ?

Exercice 2 : 20 points.
Le Paris-Nice est une course cycliste qui se déroule chaque année et qui mène les coureurs de la région parisienne à la région niçoise. L’édition 2021 s’est déroulée en 7 étapes décrites ci-dessous :

1. On étudie la série des distances parcourues par étape.

a. Calculer la distance moyenne parcourue par étape, arrondie au dixième de km.

b. Calculer la médiane des distances parcourues par étape.

c. Calculer l’étendue de la série formée par les distances parcourues par étape.

2. Un journaliste affirme : « Environ 57 % du nombre total d’étapes de cette édition se sont déroulées sur un parcours accidenté. » A-t-il raison ? Expliquer votre réponse.

3. L’Allemand Maximilian SCHACHMANN a remporté la course en 28 h 50 min.

Le dernier au classement général a effectué l’ensemble du parcours en 30 h 12 min.

Combien de retard le dernier au classement a-t-il accumulé par rapport au vainqueur ?

4. L’Irlandais Sam BENNETT a remporté la première étape en 3 h 51 min. Déterminer sa vitesse moyenne en km/h, arrondie à l’unité, lors de cette étape.

Exercice 3 : 21 points.

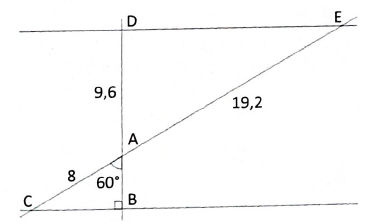
On considère la figure suivante, où toutes les longueurs sont données en centimètre.

Les points C, A et E sont alignés et les points B, A et D sont alignés.

La figure n’est pas représentée en vraie grandeur.

1. Prouver que le segment [AB] mesure 4 cm.
2. En utilisant la question précédente, démontrer que les droites (BC) et (DE) sont parallèles.
3. En déduire que la droite (DB) est perpendiculaire à la droite (DE).
4. Calculer l’aire du triangle ADE arrondie à l’unité.

Exercice 4 : 15 points.

Dans cet exercice, toutes les longueurs sont exprimées en pixel.

Partie A :

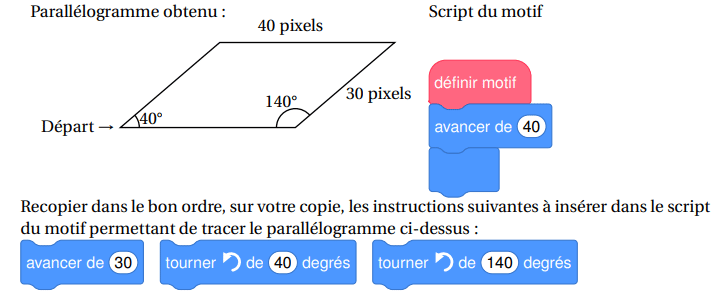
Un professeur donne à ses élèves un motif en forme de parallélogramme et le script, en partie rédigé, qui permet de tracer ce motif. On précise que le lutin est au point de départ, comme indiqué sur la figure ci-dessous, et qu’il est orienté vers la droite :

Partie B :

Le professeur demande ensuite à ses élèves d’intégrer ce script dans un programme de leur choix permettant de tracer des figures composées de plusieurs de ces motifs.

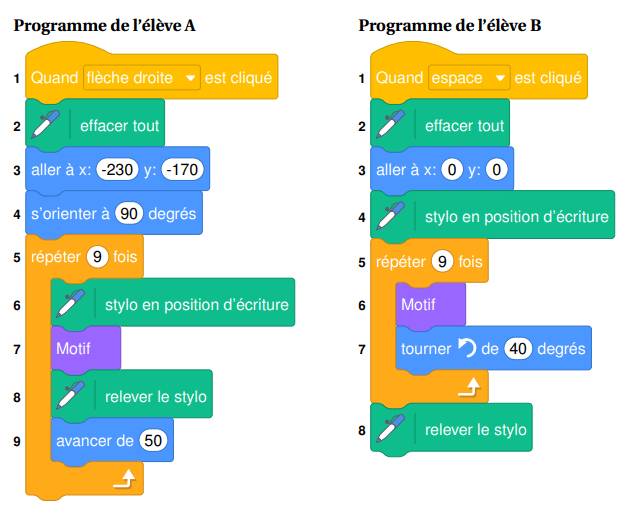
Voici les programmes écrits par deux élèves.

On rappelle que « s’orienter à 90 » signifie que l’on est orienté vers la droite.

1.Quelle action au clavier permet de lancer le programme de l’élève B ?

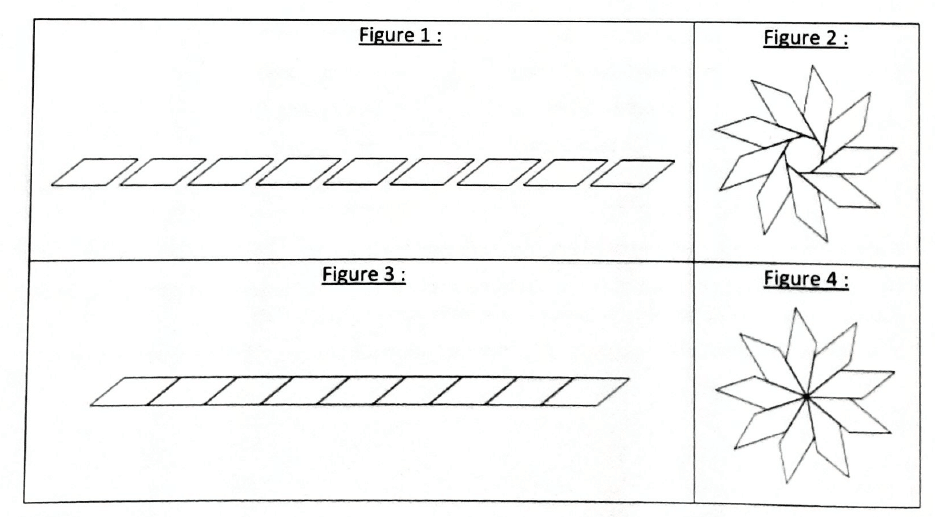
2. Parmi les figures suivantes, indiquer, ici sans justifier .

a. laquelle est obtenue avec le programme de l’élève A ?

b. laquelle est obtenue avec le programme de l’élève B ?

Exercice 5 : 25 points.

Pour fêter les 25 ans de sa boutique, un chocolatier souhaite offrir aux premiers clients de la journée une boîte contenant des truffes au chocolat.

1. Il a confectionné 300 truffes : 125 truffes parfumées au café et 175 truffes enrobées de noix de coco.

Il souhaite fabriquer ces boîtes de sorte que

Le nombre de truffes parfumées au café soit le même dans chaque boîte ;
Le nombre de truffes enrobées de noix de coco soit le même dans chaque boîte ,
Toutes les truffes soient utilisées.

a. Décomposer 125 et 175 en produit de facteurs premiers.

b. En déduire la liste des diviseurs communs à 125 et 175.

c. Quel nombre maximal de boîtes pourra-t-il réaliser ?

d. Dans ce cas, combien y aura-t-il de truffes de chaque sorte dans chaque boîte ?

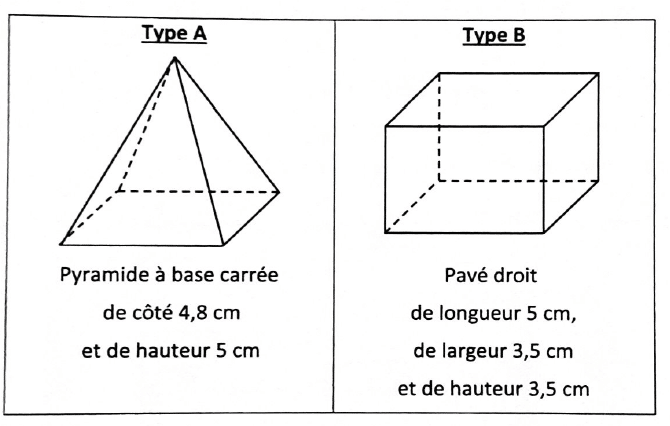
2. Le chocolatier souhaite fabriquer des boîtes contenant 12 truffes.

Pour cela, il a le choix entre deux types de boîtes qui peuvent contenir les 12 truffes, et dont les caractéristiques sont données ci-dessous :

Dans cette question, chacune des 12 truffes est assimilée à une boule de diamètre 1,5 cm.

À l’intérieur d’une boîte, pour que les truffes ne s’abîment pas pendant le transport, le volume occupé par les truffes doit être supérieur au volume non occupé par les truffes.

Quel(s) type(s) de boîte le chocolatier doit-il choisir pour que cette condition soit respectée ?

Consulter le corrigé en ligne

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2022 aux centres étrangers : sujet et corrigé du brevet.» au format PDF.

D'autres cours et exercices à consulter

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.