Algobox et algorithmes avec des exercices de programmation.

Sommaire de cette fiche

1 Initiation à l’algorithme avec le logiciel Algobox .
2 Exercices d’algorithmique : calculatrice, tableur et algobox.

Initiation à l’algorithme avec le logiciel Algobox .

Algobox est un logiciel pédagogique d’initiation à l’algorithmique simple d’emploi.

A l’aide d’un mini-langage algorithmique en français et d’une interface simple, ce logiciel permet de concevoir des mini programmes et de tester des algorithmes simples, que l’on peut rencontrer dans l’enseignement des mathématiques au secondaire (seconde, première et terminale).

Un algorithme est un programme contenant une suite d’actions permettant d’arriver è un résultat en un nombre fini d’étapes.

Le mot algorithme vient du mathématicien arabo-musulman Al-Khawarizmi, surnommé le père de l’algèbre . Le domaine qui étudie les algorithmes est appelé l’algorithmique.

Certaines épreuves du baccalauréat S de mathématiques font intervenir des algorithmes créés par Algobox.

Le code des algorithmes se construit pas è pas è l’aide de commandes déjà prédéfinies dans le logiciel (lire, afficher, affecter, instruction si alors, boucles pour de è et tant que ) : cela permet au débutant de se concentrer principalement sur la logique algorithmique, la programmation et création de boucles plutôt que sur l’apprentissage d’une syntaxe complexe.

Une fois l’algorithme terminé, il suffit d’exécuter le programme afin de voir son rendu. AlgoBox et algorithmes permet également de comprendre des algorithmes prédéfinis.

Afin de pouvoir approcher les situations mathématiques diverses que l’on peut rencontrer au lycée,

Ce logiciel inclut aussi la possibilité d’utiliser une fonction numérique ainsi que de tracer des points et des segments dans un repère préalablement défini.

Exercices d’algorithmique : calculatrice, tableur et algobox.

Algorithme de résolution des équations du second degré.

Voici un algorithme de résolution de l’équation du second degré :

$ax^2+bx+c\,(a\neq0)$

Entrées :

Saisir a,b,c (a non nul)

Traitement :

D prend la valeur

Afficher D

Si D>0 alors

X prend la valeur $\frac{-b-\sqrt{D}}{2a}$

Y prend la valeur $\frac{-b+\sqrt{D}}{2a}$

Afficher X,Y

FinSi

Si D=0 alors

X prend la valeur $-\frac{b}{2a}$

Afficher X

FinSi

Si D<0 alors

Afficher « Pas de solutions »

FinSi

1. Coder cet algorithme dans un langage de programmation avec votre calculatrice ou algobox .

2. Exécuter le programme obtenu avec a=1, b= – 5 et c= 6.

Algorithme de dichotomie.

f est la fonction sur [0;1] par :

1. Tracer la courbe représentative de f à l’écran de votre calculatrice.

2. On considère l’algorithme ci-dessous :

Initialisations :

a prend la valeur 0

b prend la valeur 1

Traitement :

Tant que b-a > 0,01

m prend la valeur $\frac{a+b}{2}$

Si f(m)>0 alors

b prend la valeur m

sinon

a prend la valeur m

FinSi

FinTantque

Sorties :

Afficher a,b

1. Expliquer le rôle de cet algorithme .

2. La condition b-a>0,01 qui gère la boucle peut-elle être modifiée ?Expliquer.

3.a. Traduire cet algorithme dans un langage de programmation avec algobox ou votre calculatrice.

b. Saisir le programme obtenu à la calculatrice ou à l’ordinateur.

c. Vérifier le fonctionnement du programme.

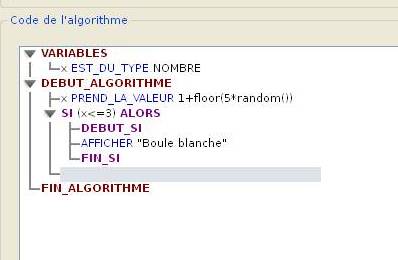
Simuler une expérience aléatoire.

Une urne contient 3 boules blanches et 2 boules noires.

On tire au hasard une boule de l’urne et on note sa couleur.

Le programme suivant, écrit avec le langage Algobox, réalise une simulation de cette expérience aléatoire.

1. Expliquer le test réalise dans ce programme.

2. Finaliser ce programme afin qu’il corresponde à l’énoncé.

3.a. Saisir ce programme à l’ordinateur.

b. Vérifier le fonctionnement du programme.

Programmer une fonction.

Soit f est la fonction polynôme de degré 2, de forme canonique

On se propose d’écrire un programme qui calcule l’image par la fonction f

d’un nombre réel donné.

1. Calculer l’image pour x=0; x=3 .

2. Ecrire ce programme avec algobox et vérifier vos résultats.

Indication :

La racine de 7.

On considère l’algorithme ci-après .

1. Faire fonctionner cet algorithme : on pourra effectuer quatre itérations.

On notera les valeurs de a et b obtenues après chaque itération.

2. Quel est le rôle de cet algorithme ?

3. Construire le programme associé avec le tableur, la calculatrice ou algobox.

4. Indiquer l’encadrement donné par le programme .

Initialisations :

a prend la valeur 2.

b prend la valeur 3.

Traitement :

Tant que $b-a>10^{-3}$

m prend la valeur $\frac{a+b}{2}$

Si alors

a prend la valeur m

sinon

b prend la valeur m

FinSi

FinTantque

Sorties :

Afficher a,b .

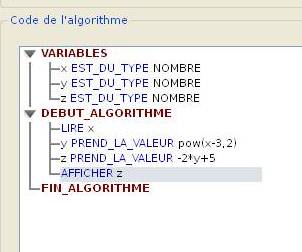
Distance entre réels.

Ecrire un algorithme

qui lit deux nombres réels x et y et

qui affiche la distance entre ces deux nombres .

Les inéquations.

a. On considère l’inéquation $6x+7\geq\, 0$ .

Résoudre cette inéquation en suivant pas à pas les instructions de l’algorithme suivant :

Retrancher 7 dans les deux membres .
Diviser par 6 les deux membres .
Ecrire l’ensemble des solutions .

b. Ecrire un algorithme de résolution de l’inéquation :

Comparer deux nombres.

Algorithme pour comparer et .

et désignent des réels.

1. On considère l’algorithme :

Entrées:

Saisir x,y

Traitement :

prend la valeur .

prend la valeur

Sortie :

Afficher .

Questions :

a. Ecrire le programme correspondant avec la calculatrice .

b. Conjecturer la comparaison de et suivant les valeurs de et .

2. Démonstration :

a. Développer et réduire .

b. En déduire la comparaison du carré de la somme de deux réels avec la somme de leurs carrés.

Définir une fonction.

Voici un algorithme :

1. Lire ( nombre non nul).

2. Donner à la valeur .

3. Donner à la valeur $\frac{1}{u}$ .

Quelle est la fonction définie par cet algorithme ?

Comparer deux réels.

Un algorithme pour comparer deux réels :

Ecrire un algorithme qui lit un nombre non nul et

qui affiche suivant les valeurs de x le plus grand des deux nombres et $\frac{1}{x}$ .

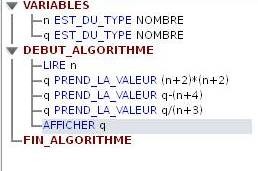
Conjecture sur un algorithme.

Voici la copie d’écran du logiciel Algobox .

1. Tester cet algorithme avec n = 4, puis n = 7.

2. Un élève a saisi n = – 3.Que se passe t’il pourquoi ?

3. Emettre une conjecture sur le résultat fourni par cet algorithme.

4. Démontrer algébriquement cette conjecture .

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «algobox et algorithmes avec des exercices.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 081 147 cours et exercices de maths téléchargés en PDF.