Probabilités : corrigé des exercices de maths en terminale en PDF.
Mis à jour le 17 septembre 2025
Exercice 2 :
Exercice 3 :
Exercice 17 :
1.
2. a. 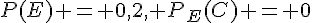
b. 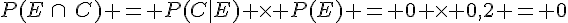 .
.
On en déduit que la probabilité d’avoir un texte connu et en espagnol est nulle.
Exercice 18 :
1.
2. P (la question porte sur la musique et Robin ne répond pas correctement) = P(B) 
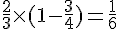 .
.
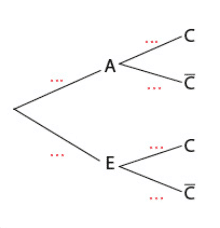
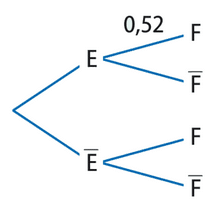
Exercice 19 :
1.
2. 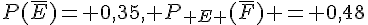 et
et 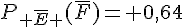 .
.
3. La probabilité d’avoir E et F en même temps est égale à  .
.
4.  ;
; 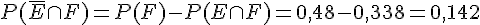 ;
; 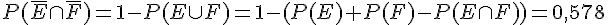 .
.
Exercice 20 :
1. a. 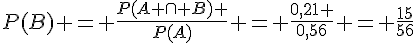 .
.
b. 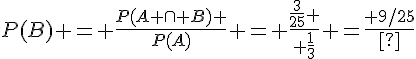 .
.
Exercice 21 :
1. P(T) = 0,84, P(O) = 0,75, 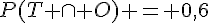 .
.
Donc, 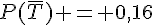 et
et 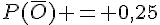 .
.
2.
| | T | 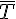 | Total |
| Total |
|——–|————|—————-|———|
| O | 0,6 | 0,15 | 0,75 |
| 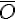 | 0,24 | 0,01 | 0,25 |
| 0,24 | 0,01 | 0,25 |
| Total | 0,84 | 0,16 | 1 |
3. 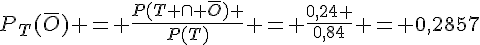 (arrondi à 4 décimales).
(arrondi à 4 décimales).
4. 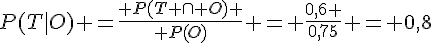 .
.
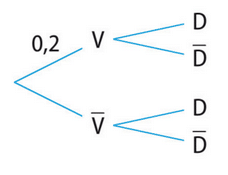
Exercice 22 :
1. P(V) = 0,2, P_V(D) = 0,96 et 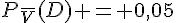 .
.
2.
3. 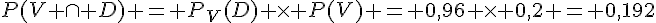 .
.
Cette probabilité représente la proportion d’ordinateurs infectés par un virus pour lesquels le logiciel antivirus détecte la présence d’un virus.
Exercice 23 :
1. 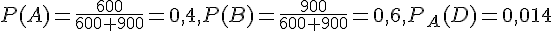 et P_B (D) = 0,024.
et P_B (D) = 0,024.
2.
3. a. 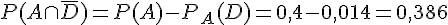 et
et 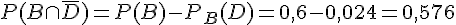 .
.
Ces probabilités représentent la proportion de composants non défectueux produits par chaque unité.
b. 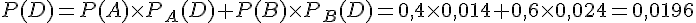 .
.
4. 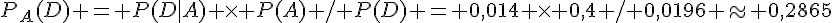 (arrondi à 4 décimales).
(arrondi à 4 décimales).
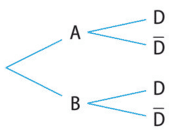
Exercice 24 :
1. P(A et B) = P(A) * P(B) = 0,8 * 0,75 = 0,6.
2. 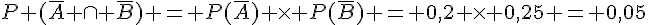 .
.
Cette probabilité correspond à la proportion de fois où ni le père ni la mère ne répondent à l’appel d’Agathe.
Exercice 25 :
1. a. 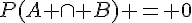 car A et B sont incompatibles.
car A et B sont incompatibles.
Donc, 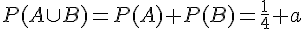 .
.
En résolvant cette équation, on trouve que 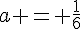 .
.
b. P(A \cap B) = P(A) * P(B) car A et B sont indépendants.
Donc,
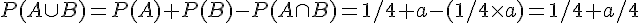 .
.
En résolvant cette équation, on trouve que a = 1/3.
c. Si A est une partie de B, alors P(A) est inférieur ou égal à P(B).
On sait que  , donc
, donc 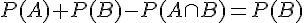 , c’est-à-dire
, c’est-à-dire 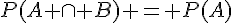 . Donc,
. Donc, 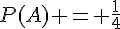 et P(B) = 1/3.
et P(B) = 1/3.
2. 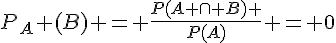 car A et B sont incompatibles dans le premier cas ;
car A et B sont incompatibles dans le premier cas ;
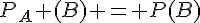 car A et B sont indépendants dans le deuxième cas ;
car A et B sont indépendants dans le deuxième cas ;
 car A est une partie de B dans le troisième cas.
car A est une partie de B dans le troisième cas.
On trouve ainsi 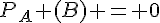 , 1/3 et 1/4 respectivement.
, 1/3 et 1/4 respectivement.
 car A et B sont incompatibles dans le premier cas ;
car A et B sont incompatibles dans le premier cas ; 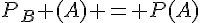 car A et B sont indépendants dans le deuxième cas ;
car A et B sont indépendants dans le deuxième cas ; 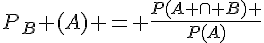 car A est une partie de B dans le troisième cas. On trouve ainsi
car A est une partie de B dans le troisième cas. On trouve ainsi 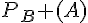 = 0, 1/4 et 1 respectivement.
= 0, 1/4 et 1 respectivement.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «probabilités : corrigé des exercices de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.