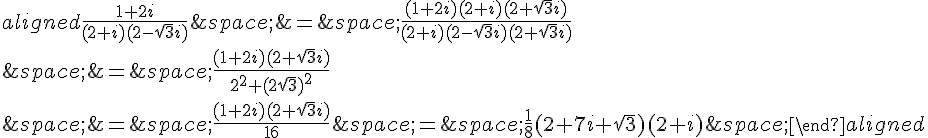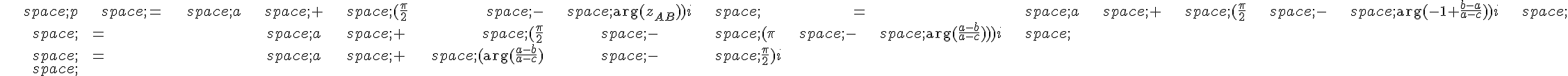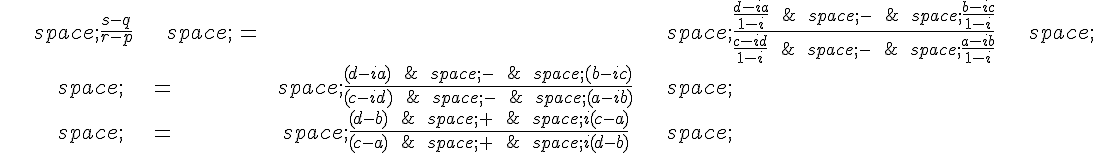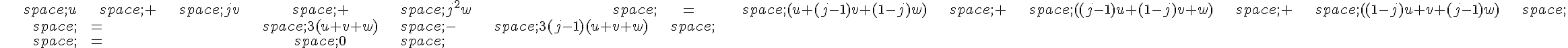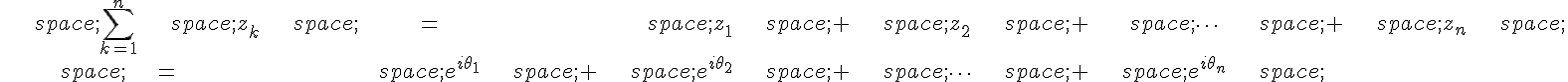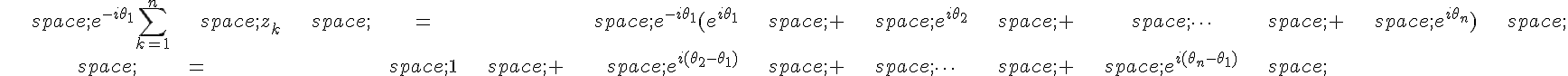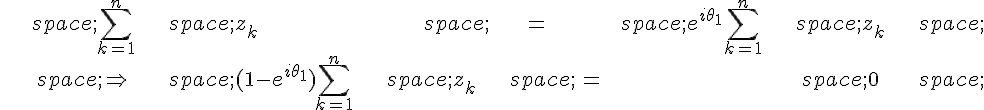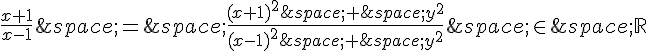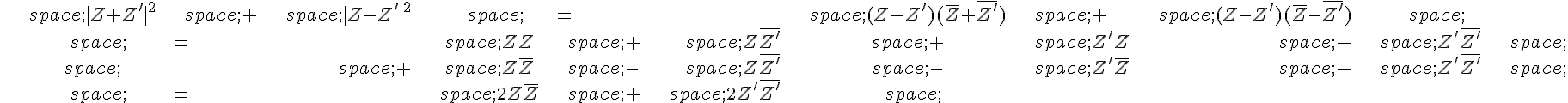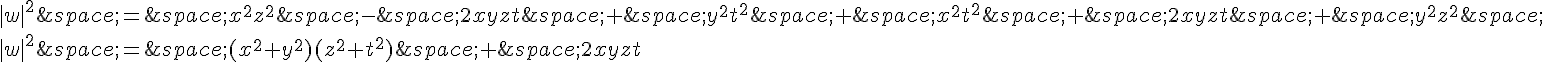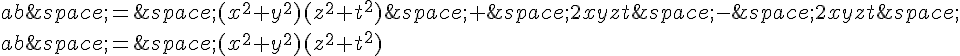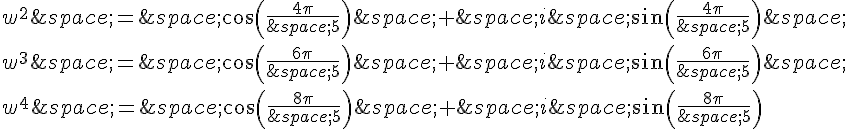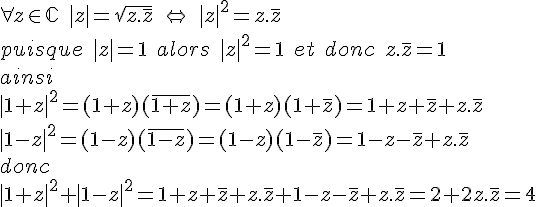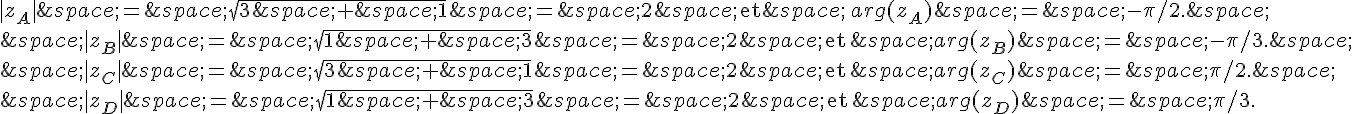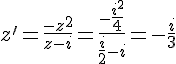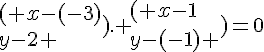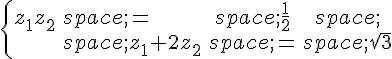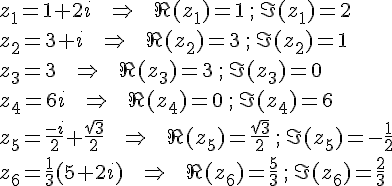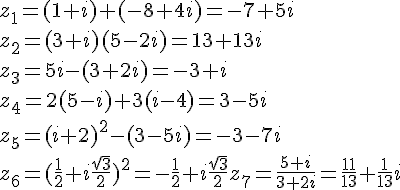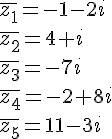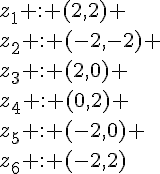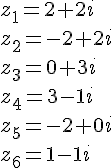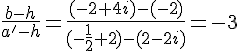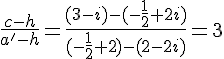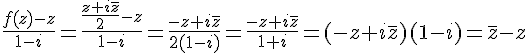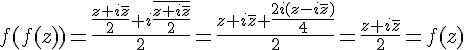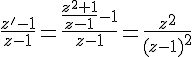Nombres complexes : corrigés des exercices de maths en terminale en PDF.
Mis à jour le 16 septembre 2025
Exercice 1 :
1.
On a , donc
.
Donc peut être mis sous la forme a + bi avec a = 11 et b = -13.
2.
On a .
Donc peut être mis sous la forme a + bi avec a = 0 et b = -1.
3.
On a
Donc peut être mis sous la forme
avec
et
.
4.
On a
Donc peut être mis sous la forme a + bi avec a = 1 et b = 1.
5.
On a
Donc peut être mis sous la forme a + bi avec a = 2 et b = 3.
6.
On a
Donc peut être mis sous la forme a + bi
avec et b = 0.
Exercice 2 :
1.
La partie réelle de z est x et la partie imaginaire de z est y.
Calculons Z avec chacune des expressions données :
La partie réelle de Z est donc
et sa partie imaginaire est
2.
La partie réelle de Z est
et sa partie imaginaire est
.
3.
La partie réelle de Z est donc
et sa partie imaginaire est
4.
Maintenant, déterminons l’ensemble des points M d’affixe z tels que Z soit réel ou imaginaire pur.
Si Z est réel pur, alors sa partie imaginaire est nulle, donc
et
La première équation donne y = 1, et la deuxième donne y = 0.
Donc si Z est réel pur, soit M a une abscisse x telle que , soit M se situe sur l’axe réel.
Si Z est imaginaire pur, alors sa partie réelle est nulle, donc
et
et
La première équation donne x = 0, la deuxième n’a pas de solution réelle, et la troisième n’a pas de solution réelle non plus.
Donc si Z est imaginaire pur, soit M a une ordonnée y telle que , soit M se situe sur l’axe imaginaire.
Exercice 3 :
On a .
Ensuite, .
Enfin, .
Exercice 4 :
On a P qui est le centre du carré de côté AB , ainsi P est situé sur la médiatrice de AB . De plus, la distance de P à AB est égale à la moitié de la longueur du côté du carré. Ainsi, on a :
où est le vecteur directeur de AB .
Comme AB est un côté du carré, on a |z_{AB}| = |a-b| .
Il reste à exprimer :
on a car les vecteurs
et a-c sont colinéaires.
Ainsi, on a :
En utilisant la formule pour l’argument d’un quotient, on obtient finalement :
De manière similaire, on obtiendra pour les autres points :
Maintenant, on calcule \frac{s-q}{r-p} :
On voit que le numérateur et le dénominateur sont les conjuguais de l’un de l’autre, donc leur quotient est de module 1.
Ainsi, les diagonales PR et QS sont de même longueur et sont perpendiculaires.
Exercice 5 :
Partie A :
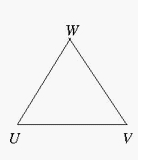
Démontrons l’équivalence UVW équilatéral de sens direct .
Supposons que UVW soit équilatéral et de sens direct.
On a alors et
.
En écrivant ces égalités en coordonnées, cela donne :
et
.
En soustrayant ces deux équations, on obtient :
ce qui prouve que UVW est bien équilatéral et de sens direct.
Supposons maintenant que .
En écrivant l’égalité en coordonnées, cela donne
.
En utilisant l’équation donnée dans l’énoncé et en simplifiant, on obtient alors :
ce qui montre l’équivalence.
Partie B :
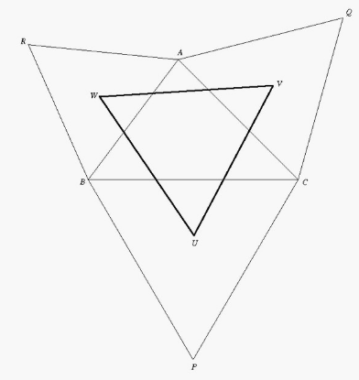
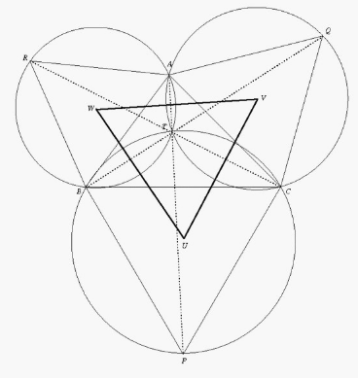
Démontrons que UVW est équilatéral avec centre de gravité G . Pour cela, notons u , v , w les affixes respectives de B , C , A dans le repère .
Alors, les affixes respectives de P , Q , R sont :
Pour trouver le centre de gravité G de UVW , on peut utiliser les formules classiques avec
où
sont les affixes de A , B , C respectivement.
Après calculs, on trouve :
Il suffit donc de démontrer que .
Or, on sait que , et de manière similaire pour q et r . Ainsi, on a :
ce qui prouve que est équilatéral avec centre de gravité G .
Finalement, il reste à montrer que G est le centre de gravité de ABC.
En utilisant les affixes de U, V, W, on peut exprimer le centre de gravité G’ de ABC :
Or, on a montré que , et on sait que j est une racine cubique de l’unité. Ainsi, en multipliant G par les racines cubiques de l’unité, on obtient G’.
Par conséquent, G est bien le centre de gravité de ABC.
Exercice 6 :
On utilise la notation où x et y sont les parties réelle et imaginaire de z , respectivement.
(1) Démontrons l’équivalence .
Si , alors Z = x et
, donc Z =
.
Réciproquement, si , alors
, donc y=0 et
.
(2) Démontrons l’équivalence .
Si , alors
si et seulement si
.
Donc si et
, alors Z = x et
.
Réciproquement, si avec r > 0 et
, alors Z n’est pas réel (sa partie imaginaire est non nulle).
Si Z = 0 , alors Z .
Sinon, si , alors Z
.
(3) Démontrons l’équivalence Z imaginaire pur .
Si Z est imaginaire pur, alors Z = iy pour un certain y , donc
.
Réciproquement, si , alors
est purement imaginaire.
Donc Z est imaginaire pur.
Exercice 7 :
1. Tout nombre complexe z vérifiant est de la forme
où
vérifie
pour un certain entier k.
Ainsi, on a pour un certain entier k.
En faisant varier k de 0 à n-1, on obtient toutes les racines nièmes de l’unité possibles, d’où .
2. Soient les racines nièmes de l’unité. On peut écrire :
où sont des réels tels que
.
On multiplie cette somme par :
Or, chaque terme de cette somme est de la forme où k varie de 2 à n.
Mais comme il y a n racines nièmes de l’unité distinctes, on en déduit que les différences sont distinctes modulo
.
Ainsi, ces termes s’annulent deux à deux, ce qui donne :
Or, le nombre est non nul car
est une racine n-ième de l’unité et donc
.
On en déduit que 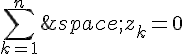
3. Chaque nombre est de la forme
, qui correspond à un angle central de mesure 2\pi/n dans le cercle trigonométrique.
Les points associés à ces nombres sont donc situés à égale distance de l’origine O, et forment un polygone régulier.
En effet, si on note l’affixe de
, alors on a :
pour tout k, où les indices sont pris modulo n.
Ainsi, les points A_k forment un polygone régulier de n côtés.
Exercice 8 :
1. On cherche les points M tels que Z soit réel.
On a Z = (z+1)/(z-1), donc Z est réel si et seulement si z+1 et z-1 sont conjugués.
Autrement dit, s’il existe un réel t tel que z+1=t(z-1).
Cela équivaut à étant réel, c’est-à-dire imaginaire pur.
En posant avec a, b réels, on obtient le système :
(t est de module 1)
.
Cela se réécrit sous la forme :
Soit où a+1 = x et b = y.
Finalement, l’ensemble E des points M tels que Z soit réel est formé par les points M d’affixes z vérifiant :
Cela équivaut à avoir y = 0 ou x = 0 (les deux cas étant exclusifs car z est différent de 1).
2. On cherche les points M tels que |Z|=1, c’est-à-dire |z+1| = |z-1|. On peut élever au carré cette égalité et obtenir :
Ce qui signifie que z est imaginaire pur.
Ainsi, les points M du plan complexes tels que |Z|=1 sont les points M d’affixe z vérifiant z = iy pour un certain réel y.
3. On cherche les points M tels que arg(Z) = π/2 [2π], c’est-à-dire les points M tels que Re(Z) = 0 et Im(Z) > 0.
On a , donc :
et
Le point M d’affixe satisfait arg(Z) = π/2 [2π] si et seulement si :
et
La première équation est équivalente à x = 0, et la seconde équation est équivalente à y > 0 (car x-1 < 0 pour x < 0). Ainsi, l’ensemble G des points M tels que arg(Z) = π/2 [2π] est la demi-droite (OM) où O est l’origine du plan complexe et M est un point du cercle trigonométrique situé au-dessus de l’axe des abscisses.
Exercice 9 :
On développe les deux côtés de l’égalité à démontrer en utilisant la formule de distributivité pour les modules :
Or, on sait que et
.
En utilisant ces formules, on obtient :
, ce qui prouve l’égalité à démontrer.
Géométriquement, cette égalité correspond à la loi des parallélogrammes dans un repère orthonormé : si Z est un vecteur, alors Z+Z’ est le vecteur somme, Z-Z’ est le vecteur différence, et les quatre termes et
représentent respectivement le carré de la norme de Z, le carré de la norme de Z’, le carré de la norme de la somme
et le carré de la norme de la différence Z-Z’.
Cette égalité montre que la somme des carrés des quatre côtés d’un parallélogramme est égale à la somme des carrés de ses deux diagonales.
Exercice 10 :
On écrit tout d’abord a et b sous forme de sommes de carrés :
On a donc et
, où x, y, z et t sont des entiers relatifs.
Par la formule de distributivité pour les modules, on a aussi :
On peut donc considérer le nombre complexe , et montrer que ab est la somme de deux carrés en montrant que
s’écrit sous cette forme.
On développe w :
On obtient donc :
En utilisant la formule de distributivité du carré, on peut développer cette expression :
On a donc :
En remplaçant par son expression, on obtient :
Cela montre que ab est bien la somme de deux carrés, à savoir et
.
Exercice 11 :
1.
a) Lorsque a = 2, la transformation f est une homothétie de rapport 2 de centre O(0,3) suivie d’une translation de vecteur 3i.
Le point O est donc l’unique point invariant de f, et la transformation conserve les droites passant par O.
Les vecteurs non nuls sont donc transformés en des vecteurs colinéaires.
b) Lorsque a = -i, la transformation f est une rotation de centre 0 et d’angle pi/2 suivie d’une translation de vecteur 3i.
Le point 0 est donc l’unique point invariant de f, et la transformation conserve les distances.
Les droites et les cercles sont donc transformés en des droites et des cercles.
2. On calcule les vecteurs et
, en utilisant les coordonnées des points donnés :
On a bien AB = A’B’.
Pour démontrer qu’il existe une unique rotation r telle que r(A) = A’ et r(B) = B’, on peut considérer la somme complexe , qui doit être nulle si les deux distances sont égales et les angles orientés sont égaux modulo pi. On a :
Comme la somme est non nulle, il n’existe pas de rotation qui puisse ramener les deux vecteurs l’un sur l’autre. Par contre, on peut effectuer une composition de homothéties et de rotations qui résolve le problème.
On peut d’abord faire une homothétie de rapport -1 qui inverse le plan :
elle transforme A en -A et B en -B.
On peut alors considérer une rotation qui envoie -A sur A’ :
elle existe et est unique car les distances AB et A’B’ sont égales.
Cette rotation envoie -B sur B’ car elle envoie la droite (AB) sur la droite (A’B’).
Enfin, on peut faire une homothétie de rapport -1 qui inverse à nouveau le plan et ramène A et A’ (ainsi que B et B’) l’un sur l’autre.
La transformation globale est donc composée de deux homothéties et une rotation, et elle envoie A sur A’ et B sur B’.
On peut calculer les coordonnées du centre et de l’angle de la rotation.
Le centre de la rotation est le milieu de AB et A’B’, soit (3/2,1/2).
On calcule le vecteur u = A’B’ / AB, qui a valeur (1-i) / (1+i) = -i.
L’angle de la rotation est arg(-i) = -pi/2.
La rotation est donc une rotation de centre (3/2,1/2) et d’angle pi/2.
Exercice 12 :
1. On cherche deux nombres complexes u et v qui vérifient le système :
u + v = -1/2
uv = -1/4
On va utiliser les relations de Viète pour déterminer les solutions.
Soient x et y les solutions de l’équation polynomiale .
Alors, d’après les relations de Viète, on a :
et
Ainsi, les solutions du système initial sont les couples (u,v) qui vérifient ces équations, c’est-à-dire qui sont de la forme (x,y) ou (y,x), où x et y sont les solutions de l’équation ci-dessus.
On peut résoudre l’équation polynomiale en utilisant la formule quadratique :
Donc les solutions sont x = (-1 + i)/2 et y = (-1 – i)/2.
Les solutions du système initial sont donc :
(u,v) = ((-1 + i)/2,(-1 – i)/2) ou ((-1 – i)/2,(-1 + i)/2)
2. On considère le polynôme .
Les racines de ce polynôme sont les puissances cinquièmes des racines de l’unité, à savoir et
.
On a donc :
En évaluant P(z) pour z=1, on obtient :
Car au moins un des facteurs et
est non nul.
On a donc :
On peut aussi utiliser les formules d’Euler pour écrire :
w = cos(2π/5) + i sin(2π/5)
Donc les autres racines de l’unité d’argument 2π/5 sont :
On a donc :
En utilisant la relation cos(-θ) = cos(θ) et les formules de trigonométrie, on peut simplifier cette expression :
Et donc :
Exercice 13 :
1.
a) On a , en utilisant les formules d’Euler.
b) On a .
c) On a .
En utilisant les formules de trigonométrie pour le cosinus et le sinus de la somme, on peut en déduire :
sin(-π/4) = (sin(-π/6)cos(-π/12) + cos(-π/6)sin(-π/12)) / √2
En utilisant que cos(-π/6) = √3/2 et sin(-π/6) = -1/2, on peut simplifier ces expressions :
cos(-π/12) = (1/2) (√6 + √2)
sin(-π/12) = (1/2) (√6 – √2)
2. On a :
(√6 + √2) cos(x) + (√6 – √2) sin(x) = 2
On peut écrire cette équation sous la forme :
cos(π/4) (√6 cos(x) + √2 sin(x)) + sin(π/4) (√6 sin(x) – √2 cos(x)) = 2/√2
On reconnaît les coefficients de cos(π/4 + x) et sin(π/4 – x) dans cette expression :
cos(π/4 + x) + sin(π/4 – x) = 2/√2
On peut simplifier cette expression en utilisant que cos(π/4) = sin(π/4) = 1/√2 :
cos(π/4) cos(x) – sin(π/4) sin(x) + sin(π/4) cos(x) – cos(π/4) sin(x) = √2
Et donc :
cos(x – π/4) = √2
Les solutions dans l’intervalle [0,2π[ sont donc :
x = π/4 ou x = 7π/4
Les points images de ces solutions sur le cercle trigonométrique sont les points d’intersection entre ce cercle et la droite d’équation y = cos(x – π/4). On a :
cos(π/4) = sin(π/4) = 1/√2
Et donc la droite d’équation y = cos(x – π/4) passe par le point (1,0) sur le cercle. Les points images des solutions sont donc :
(1/√2,1/√2) et (-1/√2,-1/√2)
Exercice 14:
On considère un nombre complexe z de module 1 (|z|=1)
Montrer que :
|1 + z|² + |1 – z|² = 4
Exercice 15 :
I.1) = i ( 1 + i) =i + i² = i-1
ou =-1+i
I.2)
II.1)Z = z²-9i² = (z+3i)(z-3i)
II.2)Z = (z-i)(z+i
)
II.3) Remarquer que -1 =i² alors
III.1) C’est une translation de vecteur d’affixe a.
Pour III.2 et III.3, de manière générale la transformation associée à la fontion z –> az (a appartenant à C) est la rotation de centre O et d’angle arg(a).
III.2) Ici arg(-1) = , donc la transformation considérée est la rotation de centre O et d’angle pi. C’est donc une symétrie de centre O.
III.3) Ici arg (i) = pi/2 donc la transformation considérée est la rotation de centre O et d’angle
Exercice 16 :
1) La rotation de centre O et d’angle 2π/3 envoie le point A sur le point B si on tourne dans le sens direct. L’affixe de B est donc obtenue en multipliant
par
:
La rotation de centre O et d’angle 2π/3 envoie le point B sur le point C si on tourne dans le sens direct. L’affixe de C est donc obtenue en multipliant
par
:
2.
a) Les points A, B et C sont situés sur le cercle (C ) de centre O et de rayon 1. De plus, d’après les calculs précédents, on a et
qui sont trois racines cubiques de l’unité distinctes.
Donc le triangle ABC est équilatéral et (C ) est son cercle circonscrit.
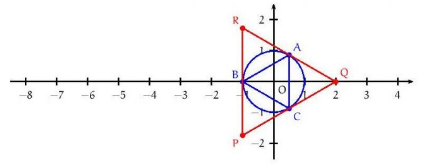
Pour construire A, B et C, on peut tracer le cercle (C ) de centre O et de rayon 1, puis repérer le point A d’affixe en tournant dans le sens trigonométrique d’un angle de π/3.
On peut ensuite construire le point B en tournant dans le sens trigonométrique d’un angle de 2π/3 à partir du point A, et le point C en tournant dans le même sens d’un angle supplémentaire de 2π/3 à partir du point B.
b) Le triangle ABC est équilatéral car ses trois côtés ont la même longueur 1.
En effet, les distances entre les points A, B et C sur la circonférence du cercle (C ) sont égales à un tiers de la longueur du cercle (C ), qui est 2π, donc égale à (2π)/3.
3.
a) L’homothétie de centre O et de rapport −2 envoie le point A sur le point P tel que OP = 2OA, donc l’affixe de P est donnée par
.
De même, elle envoie le point B sur le point Q tel que OQ = 2OB, donc l’affixe de Q est donnée par
et elle envoie le point C sur le point R tel que OR = 2OC, donc l’affixe
de R est donnée par
.
b) Le triangle PQR est équilatéral car ses trois côtés ont même longueur .
4.
a) L’homothétie de centre O et de rapport −2 est représentée par la fonction f : z ↦ -2z. Son écriture complexe est donc f(z) = -2z.
b) On a .
Soit M le milieu du segment [QR]. On a :
Donc le point M a pour affixe -1/2.
On a montré que A a pour affixe .
Comme , on en déduit que le segment [AM] est un diamètre du cercle (C ).
Donc la droite (QR), qui est la droite passant par les milieux des côtés du triangle équilatéral ABC, est perpendiculaire au diamètre [AM] et donc tangente au cercle (C ).
Exercice 17 :
Partie A.
1) Le module de z’ est donné par :
La relation entre les arguments de z et z’ est donnée par :
2) Les points O, M et M’ sont alignés si et seulement si l’argument de la différence M’ – O est égal à l’argument de la différence M – O. Or on a :
Donc l’argument de M’ – O est l’opposé de l’argument de z. Donc les points O, M et M’ sont alignés.
3) On a :
Partie B.
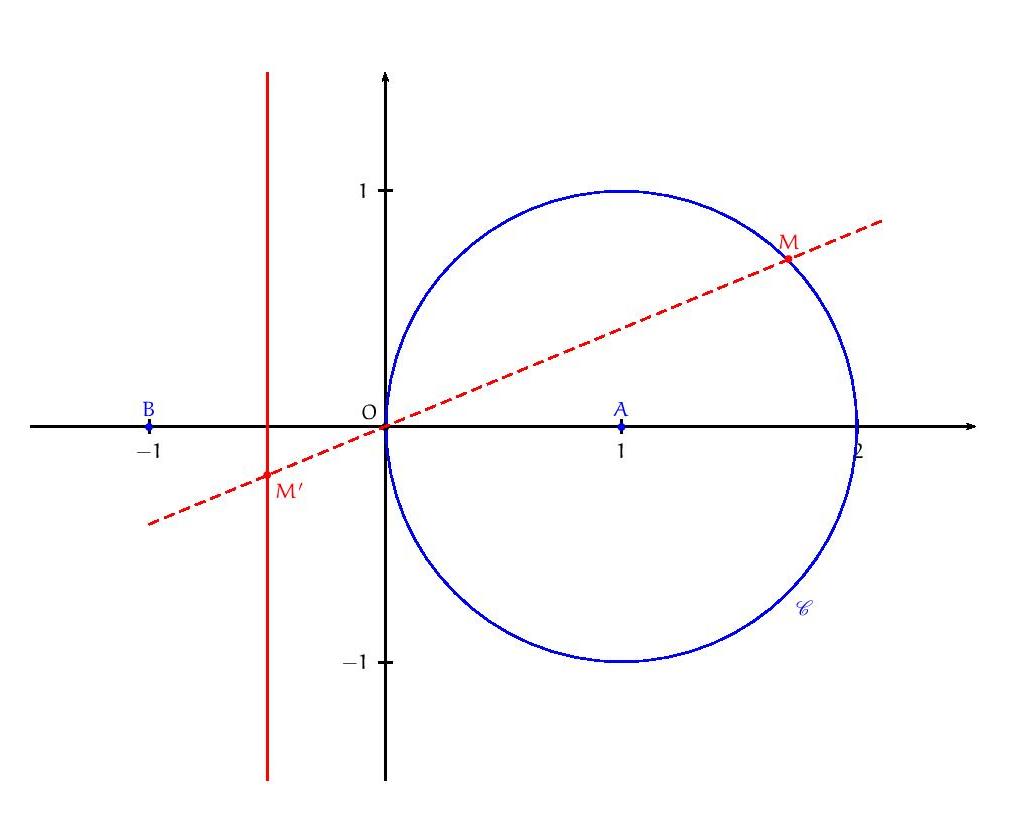
1) L’ensemble C est le cercle de centre 1 et de rayon 1.
En effet, l’équation |z – 1| = 1 signifie que le point M est à distance 1 du point 1, donc il est sur le cercle de centre 1 et de rayon 1.
2) a) On a :
D’autre part, on a :
Donc
Géométriquement, cela signifie que les points M’, O et le conjugué de M’ par rapport à O sont alignés.
b) Non, cela n’est pas vrai. Par exemple, si z = -i, alors z’ = i, et |z’ + 1| = 2 ≠ 1 = |z – 1|.
3) L’ensemble C est le cercle de centre 1 et de rayon 1. On peut le tracer en utilisant le cercle trigonométrique de centre O et de rayon 1, et en repérant le point 1 sur le cercle.
Si M est un point de C d’affixe z, alors le point M’ est le point d’intersection entre la droite (OM) et le cercle trigonométrique de centre O et de rayon 1.
On peut donc le construire en traçant la droite (OM) et en cherchant son point d’intersection avec le cercle trigonométrique, ou en utilisant la propriété géométrique énoncée dans la question 2a).
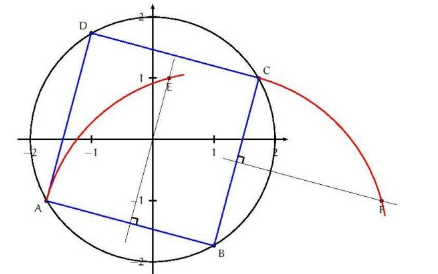
Exercice 18 :
Partie A
La démonstration demandée est la suivante : soit M un point de coordonnées (x,y) dans le repère . On note M’ le point image de M par la rotation r d’angle α et de centre Ω d’affixe ω. On a :
– Le vecteur et son image
ont la même direction car r est une rotation.
– La longueur de est la même que celle de
car r est une rotation.
– L’angle (,
) est égal à α car r est une rotation d’angle α.
– est obtenu à partir de
en multipliant cette dernière par e^{i\alpha}.
– Soit z l’affixe de M et z’ l’affixe de M’ dans le repère .
On a en identifiant les vecteurs
et
.
Ce qui donne l’écriture complexe recherchée : .
Partie B
3.
1. a. Les modules et arguments sont :
b. Pour construire A, on part du point O, on avance de unités dans la direction de -i, puis on avance d’une unité dans la direction de -1.
Pour construire B, on part du point O, on avance d’une unité dans la direction de -1, puis on avance de √3 unités dans la direction de -i.
Pour construire C, on part du point O, on avance de unités dans la direction de -i, puis on avance d’une unité dans la direction de 1.
Enfin, pour construire D, on part du point O, on avance d’une unité dans la direction de 1, puis on avance de unités dans la direction de -i.
c. Le quadrilatère ABCD est un losange car ses diagonales AC et BD ont même longueur (4) et elles sont perpendiculaires (produit scalaire nul de leurs vecteurs directeurs).
2.
a. Pour construire E, il suffit d’appliquer la rotation r d’angle -π/3 et de centre B au point A, c’est-à-dire de construire le point M d’affixe , puis de construire l’image de M par la rotation r.
On peut faire de même pour construire F à partir de C.
b. L’écriture complexe de r est , car elle envoie B sur elle-même et A sur le point d’affixe
.
c. Pour déterminer l’affixe du point E, on calcule :
Donc l’affixe du point E est .
Exercice 19 :
1. On résout l’équation par le discriminant :
Comme le discriminant est négatif, l’équation admet deux solutions complexes conjuguées :
Sous forme trigonométrique, on a :
2.
a. La rotation de centre O et d’angle π/2 envoie les vecteurs sur des vecteurs orthogonaux.
Donc l’image de B est le vecteur orthogonal à OB, c’est-à-dire OA.
Donc l’affixe de C est .
b. La rotation de centre A et d’angle π/2 envoie les vecteurs sur des vecteurs orthogonaux.
Donc l’image de C est le vecteur orthogonal à AC, c’est-à-dire AD (qui est parallèle à OB).
On a , donc l’affixe de D est
i.
c. On peut placer les points C et D sur le graphique en utilisant les informations précédentes. Le quadrilatère ABCD est un rectangle, car AB et CD ont même longueur (4) et sont perpendiculaires (produit scalaire nul).
3.
a. Soit G le barycentre de (A,1), (B,-1) et . On a :
En utilisant et en développant, on obtient :
b. G_\alpha est à l’intérieur du segment [AB] si et seulement si son coefficient de barycentre est positif, c’est-à-dire si et seulement si :
Donc l’ensemble des points est l’ensemble des points intérieurs au segment [AB] et tels que 2 < α < -1/2.
Cet ensemble est le segment de droite [FG] où F est le point d’intersection de la droite (AB) avec l’axe des ordonnées (car α = -1/2 correspond justement à l’abscisse de F).
c. On a si et seulement si
est à égale distance de A, B et C, c’est-à-dire si et seulement si c’est le centre du cercle circonscrit à ABC. Or les points A, B et C ne sont pas alignés car AB = 4 et
.
Donc il n’y a pas de tel valeur de α.
4.
On a :
où sont les coordonnées de M.
On cherche donc les points M tels que cette expression soit égale à .
On peut exprimer x et y en fonction de , puis utiliser la condition
où t’ et t » sont les longueurs des deux autres racines carrées.
On trouve une famille de droites et quelques points d’intersection avec le domaine de définition de M, qui est l’intérieur du carré d’extrémités (2,-2) et (-2,2).
Exercice 20 :
Voir la figure annexe pour les constructions.
1)
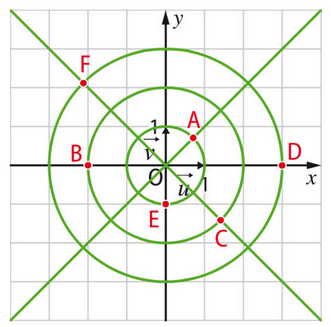
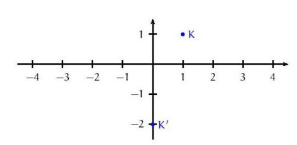
a) Le point K a pour affixe 1+i, on le place donc dans le plan complexe.
b) On calcule :
Donc l’affixe de K’ est i(1+i).
c) On place le point K’ dans le plan complexe.
2)
a) On calcule :
Donc l’affixe de L’ est -i/3. On remarque que L’ est sur la droite d’équation , perpendiculaire à la droite (OM).
b) Pour qu’un point soit invariant par f, il faut que z’ = z, c’est-à-dire :
Les solutions sont z=0 et z=1-i, donc les points d’affixes 0 et 1-i sont invariants par f.
3)
a) On sait que G est l’isobarycentre de A, M et M’, donc :
On vérifie que cette égalité est bien vérifiée pour G.
b) Si M est sur le cercle de centre A et de rayon r, alors l’affixe z vérifie |z-i|=r. On peut exprimer cela sous la forme :
On a donc une équation de cercle de centre (1,r) et de rayon .
On calcule :
Donc G est sur le cercle de centre O et de rayon 1/3r.
c) On a :
Or, on sait que les droites (AM) et (OM) font un angle θ tel que :
Donc :
Et on a :
d) On utilise les résultats des questions précédentes :
– G est sur le cercle de centre O et de rayon .
– L’affixe de D est , donc D est sur le cercle de centre A et de rayon 1/2
On construit le cercle de centre O et de rayon et le cercle de centre A et de rayon 1/2, qui se coupent en deux points E et F.
On trace la droite (EF) et on la prolonge jusqu’à couper le cercle de centre O et de rayon en G’.
On a alors , et on peut en déduire l’affixe de D’ :
– L’affixe de G’ est
– L’affixe de D’ est
On trouve ainsi que l’affixe de D’ est .
La figure annexe montre la construction des points K, K’, L’, des points invariants, du cercle de G, et du point D’.
Exercice 21 :
Soient A le point d’affixe a=1-i et B le point d’affixe b=2i-3.
A tout point M d’affixe z, avec z différent de b, on associe le point M’ d’affixe:
a) L’ensemble des points M d’affixe z tels que Z soit réel est le segment [AB].
Z est réel ssi
Cela est donc faux, c’est la droite (AB) privée de A et B .
b)Pour tout z différent de -3+2i et de -3-2i, on obtient la forme algébrique de Z par le calcul:
Ceci est faux, car elle dépend de la forme algébrique de z .
c)L’ensemble des point M d’affixe z tels que M’ soit un point de l’axe des ordonnées et le cercle d’équation , sauf le point B.
M’ est sur l’axe des ordonnées ssi
cela signifie que
Notons x la partie réelle de z et y sa partie imaginaire :
donc c’est vrai .
d) Soit z0 une solution de l’équation (on admet l’existence d’une telle solution).
Le point M0 d’affixe z0 est un point de la médiatrice de [AB]
Z= i
donc M est un point de la médiatrice de [AB] et l’affirmation est vraie .
Exercice 22 :
1. Déterminer les points invariants de f.
z’=z
z= i ou z= – i
2. a) montrer que, pour tout nombre complexe z différent de -1, (z’-1)(z+1)= – 2
b) En déduire une relation entre et
, puis entre
et
, pour tout nombre complexe z diffèrent de -1.
de même .
3. Montrer que si M appartient au cercle (C) de centre B et de rayon 2, alors M’ appartient au cercle (C’) de centre A et de rayon 1.
M appartient au cercle (C) de centre B et de rayon 2 ssi BM = 2
ssi
or
donc M’ appartient au cercle de centre A et de rayon 1 .
Exercice 23 :
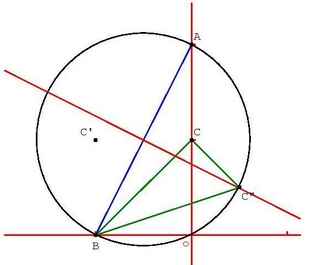
1.
a) Voir la figure ci-dessous :
b) On calcule l’affixe de C’ :
Donc l’affixe de C’ est 1-i. Le quadrilatère ACBC’ est un parallélogramme car AC est parallèle à BC’ (même argument que pour la question 3.c).
c) On cherche à résoudre l’équation z’ = i, c’est-à-dire :
Donc l’antécédent de C par f est le point d’affixe -1-i. Le triangle BCC » est isocèle en C » car C » est le milieu de [BC] (propriété de l’homothétie).
2. Le module de z’ correspond au rapport entre les distances OM’ et OM, pour tout point M différent de A. En effet, on a :
De plus, l’argument de z’ correspond à l’angle entre les vecteurs OM et OM’, mesuré dans le sens direct (sens trigonométrique), pour tout point M différent de A. En effet, on a :
3.
a) On cherche les points M tels que z’ < 0. On a :
La première inéquation est vérifiée pour z ∈ (-1, 2i), la seconde pour z ∈ (-∞,-1)∪(2i,+∞). Donc l’ensemble E_0 est la réunion de deux demi-droites :
b) On cherche les points M tels que z’ soit un imaginaire pur non nul. On a :
Donc z’ est un imaginaire pur non nul si et seulement si est un imaginaire pur non nul, c’est-à-dire s’il n’a pas de partie réelle. On a :
Donc l’équation est équivalente à l’équation
.
Le discriminant est , qui doit être négatif pour que l’équation ait une solution. Or, pour tout z non nul, on a :
Donc l’équation n’a pas de solution et est l’ensemble vide.
c) On cherche les points M tels que z’ appartienne au cercle de centre O et de rayon 1. On a :
Cela correspond géométriquement à la propriété suivante :
si M est un point du plan pour lequel la distance à -1 est égale à la distance à 2i, alors l’image M’ par f est sur le cercle de centre O et de rayon 1.
On peut remarquer que cette propriété est aussi vérifiée pour l’application g qui, à tout point M, associe le point M » d’affixe .
En effet, on a :
Donc l’ensemble correspond aux points situés sur l’axe passant par -1 et 2i.
Exercice 24 :
On cherche à résoudre le système suivant :
On peut exprimer z_1 en fonction de z_2 grâce à la deuxième équation :
En remplaçant dans la première équation, on trouve :
On résout cette équation du second degré en :
Pour chacune de ces valeurs de , on peut calculer
grâce à
.
On trouve donc deux solutions :
Pour donner les formes trigonométriques de ces nombres, on calcule leur module et leur argument :
– Pour z_1 = x_1+iy_1, on a et
si
,
ou bien si
et
,
ou bien si
et
.
– Pour , on a
et
de la même manière.
On a :
et
Donc on a :
Finalement, les deux couples (z_1,z_2) qui satisfont les conditions du problème sont :
Exercice 25 :
Exercice 26 :
1. et
.
2. .
Donc les écritures sous forme algébrique, exponentielle et trigonométrique de sont respectivement :
et
.
3. et
.
Donc
et .
Exercice 27 :
Exercice 28 :
1. Voir la figure suivante :
Tracer la figure….
2. Les affixes de A’ et B’ sont respectivement : et
.
3. , donc
. On a
et
où
.
Donc .
Ainsi .
Exercice 29 :
.
Donc les affixes de et
sont respectivement : $6-4i$ et $14-4i$.
.
Comme , le quadrilatère est un parallélogramme.
De plus, les diagonales sont et
et leur somme est
.
Donc le quadrilatère est un losange.
Exercice 30 :
1. a. On calcule et les solutions sont
et
.
Ou bien on peut utiliser la formule
.
b. On a et
.
2. a. On construit d’abord le segment [AB] de longueur .
On place les points A et P.
On trace un cercle centré en A de rayon a et un cercle centré en P de rayon (le rayon du cercle passant par A).
Ces deux cercles se coupent en deux points, on prend celui qui est à gauche de [AP]. Ce point est le point M.

b. Les affixes de A, M et P sont respectivement ,
et
.
Les affixes de B et C sont respectivement et $ai+b$.
Donc et
(car AD=AM=BM=BD=3).
Donc l’affixe de B est et l’affixe de C est
.
c. et
. Donc
et le triangle ABC est rectangle.
De plus, .
Donc le triangle est isocèle en A.
d. On cherche l’affixe de D tel que AD soit orthogonal à AB. Donc , soit
, ce qui donne
ou encore
. On a aussi $AD=3$.
Donc et on substitue
en fonction de $y$ pour trouver
. Les solutions sont
et
.
Donc et
. Ainsi l’affixe de D est
ou
.
Exercice 31 :
1. et
.
et
.
et
.
et $\Im(-4)=0$.
et
.
et
.
2. et
sont des réels.
et
sont imaginaires purs.
Exercice 32 :
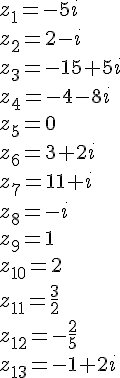
Exercice 33 :
Exercice 34 :
Exercice 35 :
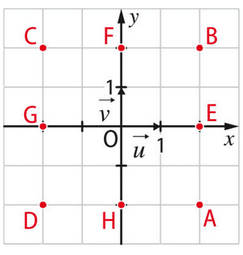
Les points images sont :
Exercice 36 :
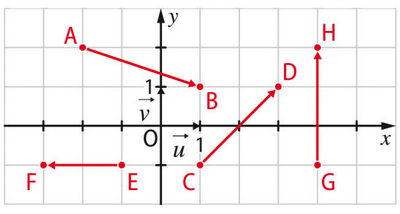
Les affixes qui correspondent à chaque vecteur sont :
Exercice 37 :
1. Voir la figure suivante :
On a :
.
2. Donc .
Exercice 38 :
Les formes trigonométriques d’un nombre complexe sont de la forme avec r le module de z et
son argument.
est une forme trigonométrique.
est une forme trigonométrique.
est une forme trigonométrique.
est une forme algébrique.
Exercice 39 :
On utilise les formules pour le produit, le quotient et la puissance de nombres complexes en forme trigonométrique :
1) On a :
2) On a :
Exercice 40 :
On utilise la formule d’Euler pour passer d’une forme exponentielle à une forme trigonométrique :
Exercice 41 :
1) On a :
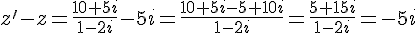
2) On a :
Exercice 42 :
On multiplie le numérateur et le dénominateur par le conjugué du dénominateur pour éliminer le terme imaginaire au dénominateur :
Exercice 43 :
a) On a :
b) On a :
c) On a :
d) On a déjà calculé \frac{z_1}{z_2} à la question c).
e) On a :
f) On a :
Exercice 44 :
On remarque que , donc la suite des puissance de i suit un cycle de période 4 :
Exercice 45 :
On a :
Pour n pair, on a
Pour n impair, on a
On calcule :
On a donc bien vérifié la relation d’équivalence pour les racines cubiques de l’unité.
Pour la somme S’, on remarque que suit un cycle de période 6, donc :
Exercice 46 :
On a :
Donc 2+i et 2-i sont les racines du polynôme P, et donc les formes algébriques de ces racines.
Exercice 47 :
1.a) On peut placer les points A, B, C et H sur une figure. Le point V est le milieu de [AB], donc on le trouve facilement.
On peut alors construire le cercle en passant par les points A,B et C. On trouve que le rayon de ce cercle est 5.
Le point H, quant à lui, ne nous sert pas pour cette question et sera utile pour la suite.
b) Pour montrer que V est le centre du cercle circonscrit au triangle ABC, il suffit de montrer que les trois médiatrices du triangle ABC sont concourantes en V.
La médiatrice d’un segment est la droite perpendiculaire à ce segment passant par son milieu.
La médiatrice du segment [AB] est la droite d’équation.
La médiatrice du segment [BC] est la droite d’équation y=2x+5.
La médiatrice du segment [CA] est la droite d’équation .
Ces trois droites sont effectivement concourantes en V(1,2), donc V est bien le centre du cercle circonscrit au triangle ABC.
c) On a :
Pour que les droites (AH) et (BC) soient perpendiculaires, il faut que leur coefficient directeur ait un produit égal à -1.
Or le coefficient directeur de la droite (AH) est et celui de la droite (BC) est
, donc leur produit est bien égal à -1.
2.a) On a :
On peut donc placer le point G sur la figure.
b) Pour montrer que les droites (GV), (GH) et (GK) sont concourantes, il suffit de montrer que le point G appartient à la droite d’Euler du triangle ABC.
On sait que la droite d’Euler passe par les points G, H et V, donc il suffit de montrer que les trois sont alignés.
On a déjà montré que V est le centre du cercle circonscrit au triangle ABC et que H est l’orthocentre du triangle ABC.
La droite (GV) est la droite passant par les points A et B, donc elle coupe [HC] en K, le milieu de [AH]. Donc G, H et K sont bien alignés.
c) A’ est le milieu de [BC], donc .
On calcule :
Donc les droites (HA’) et (BC) sont bien parallèles.
Le quadrilatère KHA’V est donc un parallélogramme, car ses côtés opposés sont parallèles et égaux (les diagonales sont des segments de médiatrices).
Exercice 48 :
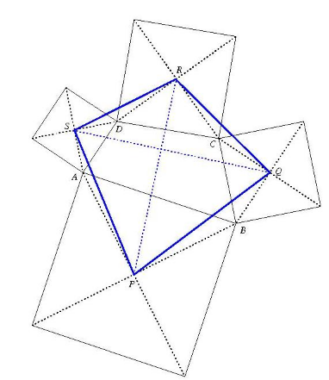
On peut placer les points A, B et C sur un cercle de rayon r centré en O, et tracer les points A’, B’ et C’ correspondants à une rotation de 60 degrés (un tiers de tour) autour de O.
Les points U, V et W sont les milieux des segments [A’B], [B’C] et [C’A].
Pour montrer que le triangle UVW est équilatéral, on peut utiliser la formule suivante pour la distance entre deux points en coordonnées complexes :
En effet, les points A’, B’ et C’ sont situés sur un cercle de même rayon r et de centre O (car la rotation préserve les distances).
On a :
Donc :
Donc :
On en déduit :
On peut de même montrer que
Donc le triangle A’B’C’ est équilatéral.
On a également :
On calcule :
Donc les trois vecteurs et
ont la même norme et des arguments égaux à 120°, donc le triangle UVW est équilatéral.
Exercice 49 :
1. On a f(z)=z si et seulement si si et seulement si
.
Donc l’ensemble des points M vérifiant f(z)=z est l’ensemble des points dont l’affixe est un réel, c’est-à-dire une droite.
2. On calcule :
Donc le nombre est réel.
3. On note M’ le point d’affixe qui est l’image de M par f. On veut montrer que M’ est sur la droite ∆ passant par M et de vecteur directeur
.
On a deux points de cette droite, O et M, et on connait son vecteur directeur.
Soit N le milieu de [OM].
Le vecteur est alors parallèle à la droite ∆, et
.
Le vecteur est donc parallèle à
, et donc M’ est sur la droite ∆.
4. On a :
5. On sait que la droite (d) est l’ensemble des points M tels que .
La droite ∆ est la droite passant par O et de vecteur directeur .
M’ est à la fois sur (d) et sur ∆, donc il est l’intersection de ces deux droites.
6. L’application f est une symétrie orthogonale par rapport à la droite (d). Autrement dit, f envoie un point M sur le symétrique de M par rapport à la droite (d).
Exercice 50 :
PARTIE A :
On a :
Le cercle est le cercle de centre A et de rayon 1, donc il est donné par l’équation
.
On calcule :
Donc appartient bien au cercle
.
On peut calculer :
On peut en déduire que la mesure de l’angle est
, car on est en présence d’un triangle équilatéral.
Les formes exponentielles de et
sont :
Or on a :
Donc A, B et E sont alignés.
PARTIE B :
Soit z un nombre complexe tel que .
On considère la droite passant par les points A et M d’affixe z, c’est-à-dire la droite d’équation :
Cette droite passe également par le point M’ d’affixe , car M’ est l’image de M par la symétrie orthogonale par rapport à la droite (d) d’équation
.
On note P le point d’affixe 1, qui est le point d’intersection des droites (OM) et (BMP). Le point M’ est alors sur la droite (OM’) et on a :
Donc est le rapport des distances PM’ et PM, qui est l’argument du nombre complexe
est donc un angle orienté avec le vecteur
.
Le point M’ est donc sur la droite (AP) qui est parallèle à la droite (OM).
Si A, M et M’ sont alignés, cela signifie que le vecteur est colinéaire au vecteur
, donc que
pour un certain réel
.
On a :
Donc :
Cette équation a au plus deux solutions pour z, car c’est une équation de degré 2. Donc le point M’ peut être l’image de au plus deux points différents par f.
On a :
Donc un point M est invariant par f si et seulement si z est solution de l’équation . Cette équation a pour discriminant
, donc deux solutions dans
, qui sont :
Ces sont donc les deux points invariants de l’application f.
Si un point M est invariant par f, alors il est envoyé sur lui-même par la symétrie orthogonale par rapport à la droite (d). Autrement dit, il est symétrique de A par rapport à la droite (d).
Si , alors
, donc
.
Si , alors
, donc
.
Donc pour tout z de .
Exercice 51 :
On calcule :
Donc M est invariant par f si et seulement si .
Cette équation est équivalente à :
Cette équation a pour discriminant 49, donc deux solutions dans , qui sont :
Donc les points d’affixes et
sont les points invariants de f.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «nombres complexes : corrigés des exercices de maths en terminale en PDF.» au format PDF.
Ressources de terminale
Cours de terminale
Exercices de terminale
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.