Fonctions : corrigé des exercices en 3ème en PDF.
Mis à jour le 5 septembre 2025
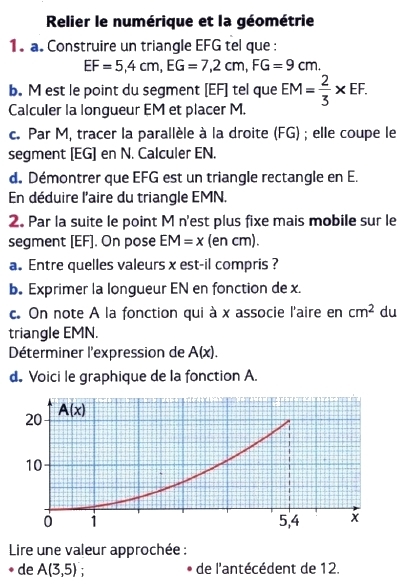
Exercice 1 :
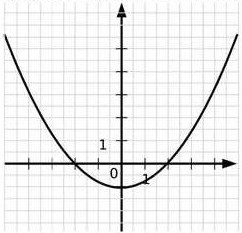
a. Nous avons h(0)= – 1.
b. Les nombres 2 et – 2 ont pour image 0 par la fonction f.
c. h(4)=3,5 et h(-3)=1,2 .
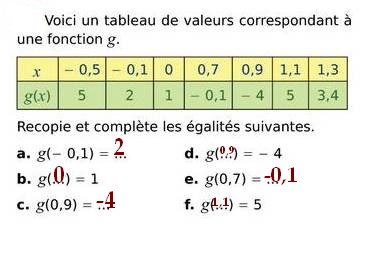
Exercice 2 :
Exercice 3 :
UNE BOITE EST FABRIQUEE DANS UNE PLAQUE DE CARTON CARREE DE 20 CM DE COTE. POUR CELA ON COUPE DES CARRES DE X CM ET ON PLIE LE LONG DES POINTILLES.
1. POURQUOI X EST COMPRIS ENTRE O ET 1O .
car la largeur des deux carrés vaut 2x si x prend la valeur maximale de 10 les deux carrés se toucheront au delà ces deux carrés n’existeront pas.
2. QUELLE EST LA HAUTEUR DE LA BOITE .
La hauteur de la boîte vaut x cm.
3. CALCULER L’AIRE A(x) DU CARRE AU FOND DE LA BOITE EN CM² .

4. CALCULER LE VOLUME V(x) DE LA BOITE EN CM3 .
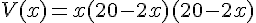
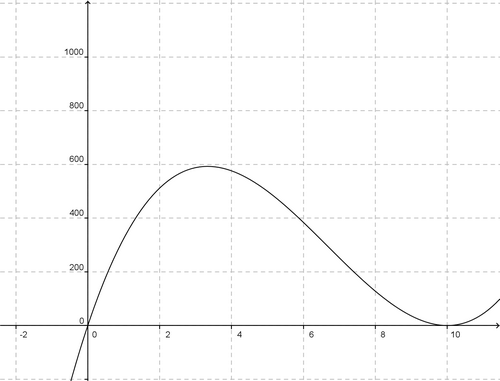
5. REPRESENTER V(x) SUR UN GRAPHIQUE POUR LES VALEURS PRECEDENTES .
6. CONJECTURER LA VALEUR X POUR LAQUELLE LE VOLUME EST MAXIMUM .
Le volume de la boîte semble être maximal pour x = 3 cm .
Exercice 4 :
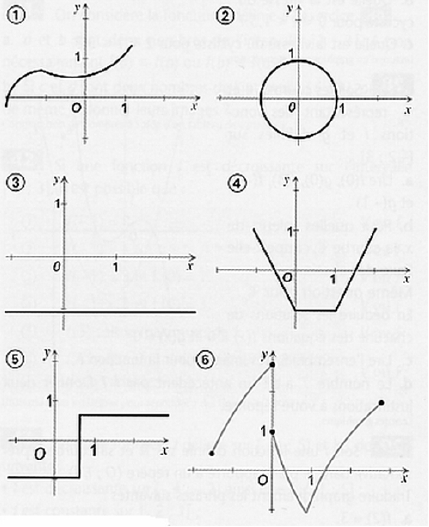
Dire si les représentations graphiques données sont, oui ou non, des représentations de fonctions :
Tout antécédent pour une fonction possède une unique image.
On en déduit que les courbes représentatives de fonctions sont les graphiques 1, 3,4 et 5.
Exercice 5 :
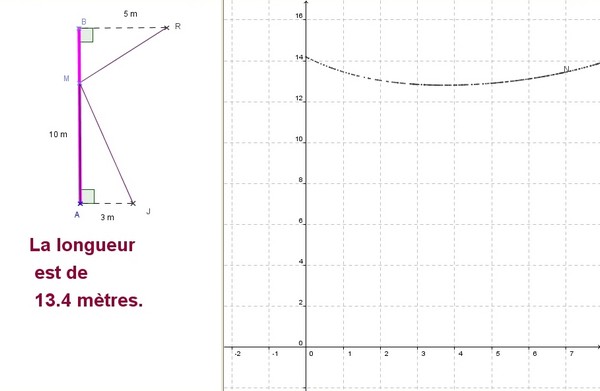
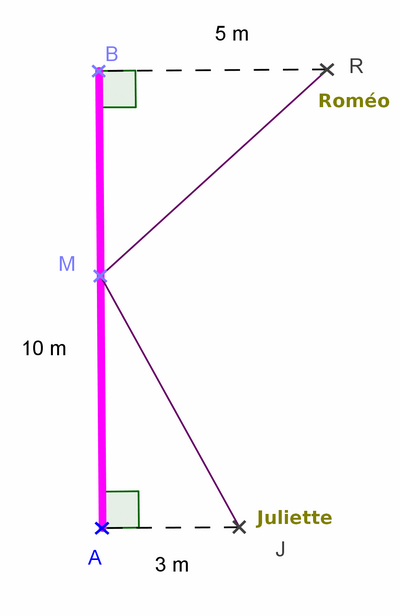
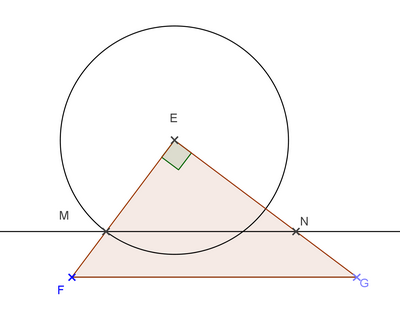
Roméo se trouve en R, Juliette en J.
Roméo doit aller cueillir une fleur sur le mur de roses [AB] et la porter à Juliette, le plus rapidement possible, donc par le chemin le plus court.
BR = 5 m , AJ = 3 m et AB=10 .
Déterminer la position du point M pour que son chemin empreinté soit le plus court.
Exprimons la longueur parcourue par Roméo :
Notons 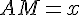 avec
avec 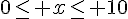
Appliquons le théorème de Pythagore dans les triangles rectangles JAM et MBR.
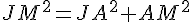 et
et 
 et
et 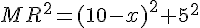
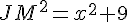 et
et 
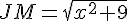 et
et 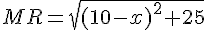
ainsi

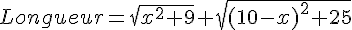
Pour la partie mathématique, on utilise Pythagore, les fonctions, les racines carrées, les fractions puis Thalès en utilisant le point J’ symétrique de J par rapport à A.
(RJ’) (AB) donne tout de suite la position recherchée.
Voici la courbe lorsque l’on fait varier le point M correspondant aux variations de la longueur
parcourue par Roméo.
Exercice 6 :
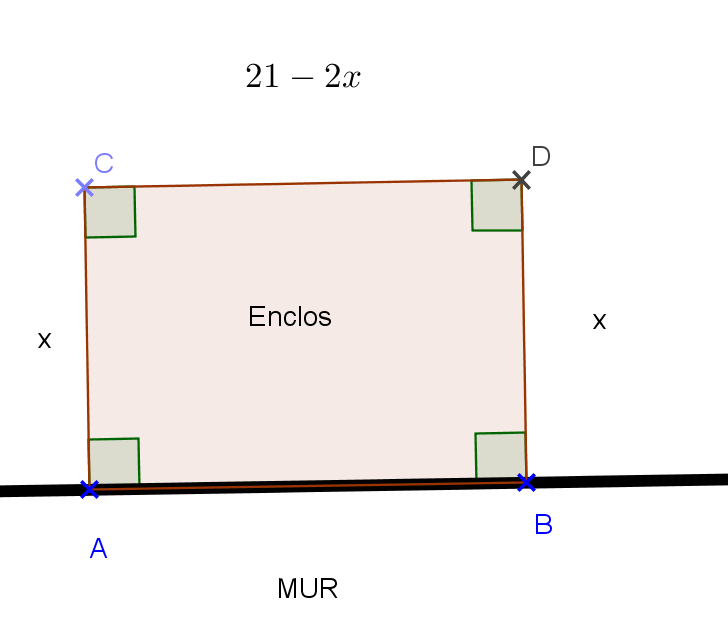
Pour son chien, Aicko, Mr Martin souhaite réaliser un enclos rectangulaire, le long de son mur.
Il dispose de 21 m de grillage.
Il veut utiliser les 21 m de grillage et donner le maximum d’espace pour Aicko. 1) a. Quelle est la longueur de l’enclos si son maître choisit une largeur de 3m ? de 7m ?
 pour une largeur de 3 m.
pour une largeur de 3 m.
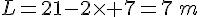 pour une largeur de 7 m.
pour une largeur de 7 m.
b. Quelle est l’aire dont dispose alors Aicko pour se débattre dans ces deux cas ?
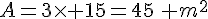 pour une largeur de 3 m.
pour une largeur de 3 m.
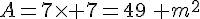 pour une largeur de 7 m. 2) Mr Martin souhaite que son chien ait le maximum d’espace.
pour une largeur de 7 m. 2) Mr Martin souhaite que son chien ait le maximum d’espace.
Notons x la largueur de l’enclos.
a. Donner un encadrement de x (quelles sont les largeurs minimales et maximales ? )
D’abord la largeur est un nombre positif donc 
de plus la longueur doit être positive
ce qui équivaut à 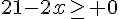
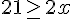


Conclusion : x doit être compris entre 0 et 10,5 mètres.
b. Exprimer, en fonction de x, la longueur de l’enclos.
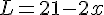
c. Prouver alors l’expression de l’aire de l’enclos en fonction de x, est 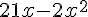 .
.
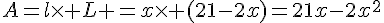
Remarque :
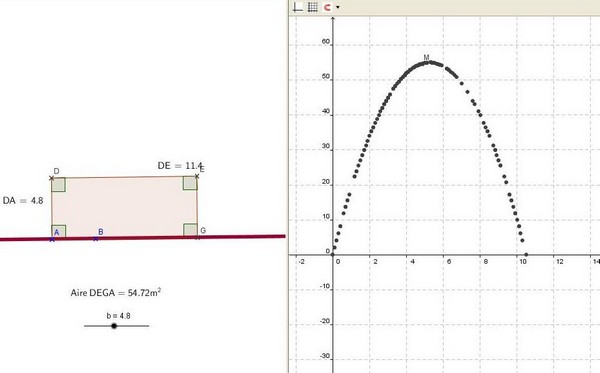
voici les variations de l’aire de la zone du chien lorsque l’on fait varier la largeur du rectangle :
Nous pourrions montrer que l’aire maximale est atteinte lorsque 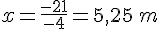
et que l’aire maximale de l’enclos est :
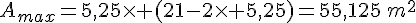
de plus la longueur vaut
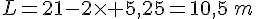
Exercice 7 :
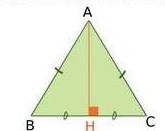
a. ABC est un triangle équilatéral
donc la hauteur (AH) est également une médiatrice, on en déduit que H est le milieu de [BC].
Dans ABH rectangle en H d’après la partie directe du théorème de pythagore :
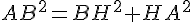
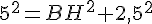
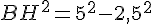
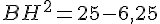
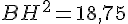

Exercice 8 :
Exercice 9 :
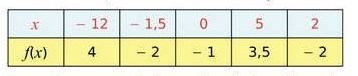
Le nombre 3,5 a deux antécédents.
Le nombre – 2 a deux antécédents.
Le nombre 2 a trois antécédents.
Exercice 10 :
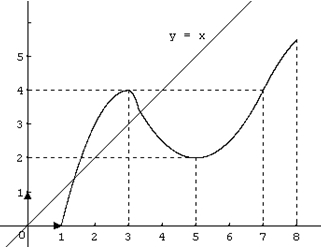
On a représenté ci-dessous :
· la droite d’équation y = x,
· la courbe représentative d’une fonction f définie sur [1 ; 8].
Les questions posées seront résolues par lecture graphique .
1. Répondre par vrai ou faux aux questions suivantes :
|
vrai ou faux |
||
| 1. | 1 a pour image 0 par la fonction f | VRAI |
| 2. | 0 a pour image 1 par la fonction f | FAUX |
| 3. | 7 est un antécédent de 4 par la fonction f | VRAI |
| 4. | 3 est un antécédent de 4 par la fonction f | VRAI |
| 5. | f(3) = 4 | VRAI |
| 6. | f(2) = 5 | FAUX |
| 7. | f(3) > f(5) | VRAI |
| 8. | 2,5 a trois antécédents par la fonction f | VRAI |
| 9. | 0,5 a un seul antécédent par la fonction f | VRAI |
| 10. | L’équation f(x) = 3 a au moins une solution dans l’intervalle [1 ; 8] |
VRAI |
| 11. | L’équation f(x) = x a au moins une solution dans l’intervalle [1 ; 8] |
VRAI |
| 12. | f est croissante sur l’intervalle [1 ; 8] | FAUX |
| 13. | Si x appartient à l’intervalle [4 ; 5], alors f(x) > x | FAUX |
| 14. | Si a et b appartiennent à l’intervalle [3 ; 5] et si a < b, alors f(a) < f(b) | FAUX |
2. Résoudre graphiquement l’inéquation : f(x) – f(3) > 0. On donnera la solution sous forme d’un intervalle.
équivaut à f(x) > f(3)
équivaut à f(x) > 4
L’ensemble solution est l’intervalle ]7;8].
Exercice 11 :
1.
b.
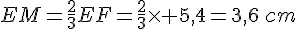
c. En utilisant le théorème de Thalès, on obtient :
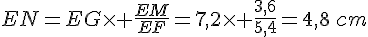
Exercice 12 :
Il existe trois variétés de thon pêché en Polynésie &ançaise :
. le thon Germon (variété de thon blanc)
. le thon Jaune (à nageoires jaunes, variété de thon rouge)
. le thon Obèse (variété de thon rouge)
1. Le graphique 1, page suivante, représente la taille du thon Germon en fonction de Sa masse’
a. Est-ce que la taille du thon germon est proportionnelle à sa masse ? Justifier.
Non, la courbe n’est pas une droite passant par l’origine donc la taille de thon germon n’est pas proportionnelle à sa masse.
b. L’équipe de Moana a capturé un thon Germon de 22 kg.
Déterminer graphiquement, sa taille.
Sa taille est de 100 cm.
c. L’équipe de Teiki a pris un thon germon de 70 cm. Déterminer graphiquement sa masse.
Sa masse est de 7 kg.
2. La masse du thon Jaune représente en moyenne 17 % de la masse totale des trois espèces de thon
pêché.
Le graphique 2, page suivante, représente la masse de thon Jaune pêché par rapport à la masse totale
de thon pêché.
a. Est-ce que la masse de thon Jaune est proportionnelle à la masse totale de thon pêché ? Justifier.
Oui car la courbe est une droite passant par l’origine du repère.
b. L’équipe de Moana a pêché 400 kg de thon. Calculer la masse de thon Jaune pêché.
La masse de thon jaune pêché est de 69 kg.
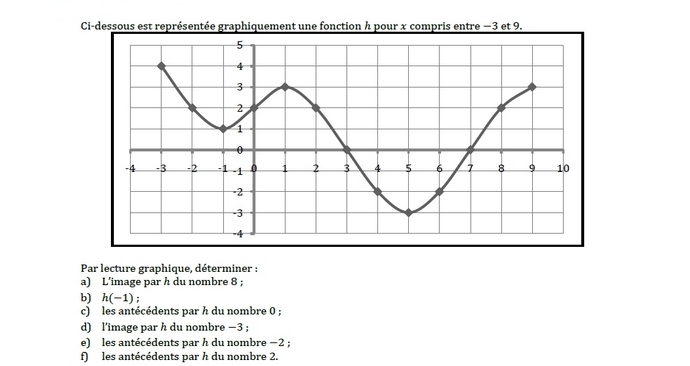
Exercice 13 :
a) h(8) = 2 .
b) h(-1)=1 .
c) Les antécédents de 0 sont x = 3 et x = 7 .
d) h(-3) = 4 .
e) Les antécédents de – 2 sont x = 4 et x = 6 .
f ) Les antécédentes sont x = -2 ; x = 0 ; x = 2 ; x = 8 .
Exercice 14 :
1 ) Non la vitesse n’a pas été constante puisque la courbe n’est pas une droite .
2) Oui le coureur s’est arrêté entre la 20 et 25ème minute .
3 ) L’image de 5 est 1.Cela signifie qu’en 5 minutes, il a parcouru 1 km .
4) L’antécédent de 6 est 35.Cela signifie qu’il a parcouru 6 km en 35 minutes .
5) Cette ascension a débuté à la 10ème minute .La longueur de cette côté est de 2 km.
6) Car la courbe est de plus en plus verticale dont il parcourt plus de distance.
7) Lors de la descente, en 10 minutes, il a parcouru 3 km
Exercice 15 :
1) 
2) ![v(6)=18\pi[(1+\frac{6}{6})-1]](https://mathovore.fr/latex-images/90a2a27e5b6b09b634e92dedd73b3c35.png)
![v(6)=18\pi[(\frac{6}{6}+\frac{6}{6})-1]](https://mathovore.fr/latex-images/db4023b026a1c3039dc65460058d62be.png)
![v(6)=18\pi[2-1]](https://mathovore.fr/latex-images/0bdb702c76ae6e8893d4191b973497f1.png)
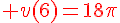
3)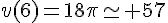
4) L’antécédent de 250 est tel que 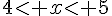 .
.

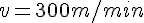
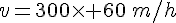
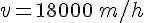
La compréhension des fonctions est essentielle pour un élève de 3ème. En effet, le chapitre sur les fonctions englobe des notions intéressantes et des méthodes de calculs pratiques et simples.
Exercice 16 :
Traduire à l’aide d’écritures simples les phrases suivantes (et réciproquement..) :
a. f(2) = 4
L’image de 2 par la fonction f est 4.
b. La courbe de la fonction f passe par le point A(4 ; −1).
L’image de 4 par la fonction f est – 1.
c. L’ordonnée du point d’abscisse 4 de la courbe C de g vaut 2.
L’image de 4 par la fonction g est 2.
d. La représentation graphique de la fonction h coupe l’axe des ordonnées au point d’ordonnée 3.
L’image de 0 par la fonction h est 3.
e. La courbe représentant la fonction k passe par l’origine.
L’image de 0 par la fonction k est 0.
f. La courbe C représentant la fonction g est au-dessus de l’axe des abscisses entre les points
d’abscisse −4 et 1.
Entre x=-4 et x=1, la fonction g est positive ou nulle.
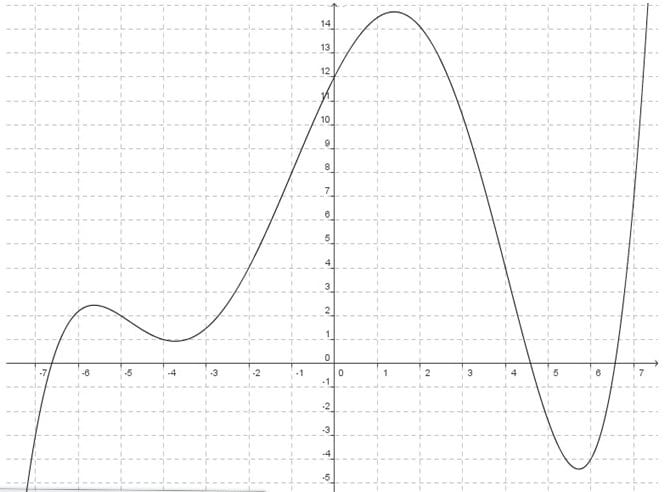
Exercice 17 :
Dans le repère ci-dessous, on note f la fonction représentée par son graphe.
1.
- Vérifier, en plaçant le point P (-7 ; -3) dans le repère, que celui-ci appartient bien à la courbe. Compléter alors la colonne du tableau ci-dessous correspondant à ce point.
- Placer dans le repère le point Q appartenant à la courbe sachant que son abscisse est -2. Compléter la colonne du tableau correspondant à ce point.
- Placer dans le repère le point R appartenant à la courbe sachant que son ordonnée est 8 et son abscisse négative. Compléter la colonne du tableau correspondant à ce point.
- Placer dans le repère, deux points S et T de votre choix appartenant à la courbe. Compléter les colonnes du tableau correspondant à ces points.
|
Points |
P |
Q |
R |
S |
T |
|
Abscisse |
x= -7 |
x = -2 |
x= -1 |
x = 4,5 |
x= 0 |
|
Ordonnée |
y = -3 |
y= 4 |
y = 8 |
y= 0 |
y =12 |
|
Relation : f(x) = y |
f (-7) =-3 |
f (-2) = 4 |
f (-1) = 8 |
f (4,5) = 0 |
f (0) = 12 |
2. Résoudre les questions suivantes graphiquement (on laissera les traits de construction apparents ) .
- Quel est l’image de – 2 par f ? f(-2)=4
- Quelle est la valeur de f (- 1 ) ?f(-1)=8
- Quel(s) est l’antécédent de – 3 ?x= – 7
- Résoudre graphiquement f (x) =7 .x=-1,2 et x=3,5
- Quel(s) nombre a pour image – 4 ?x=-7
- Quelle est la valeur de f ( – 5) ?f(-5)=2
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonctions : corrigé des exercices en 3ème en PDF.» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.