Sujet 2018 France du brevet de maths des collèges

DIPLÔME NATIONAL DU BREVET
SESSION 2018
MATHEMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 sur 100 points

L’évaluation prend en compte la clarté et la précision des raisonnements ainsi que, plus largement, la qualité de la rédaction. Elle prend en compte les essais et les démarches engagées, même non aboutis.

Exercice 1 (11 points)
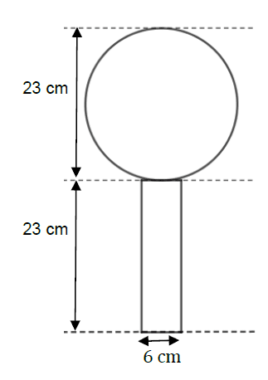
Le gros globe de cristal est un trophée attribué au vainqueur de la coupe du monde de ski. Ce trophée pèse 9 kg et mesure 46 cm de hauteur.
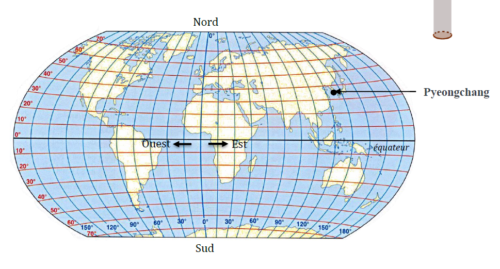
1. Le biathlète français Martin Fourcade a remporté le sixième gros globe de cristal de sa carrière en 2017 à Pyeongchang en Corée du Sud.

Donner approximativement la latitude et la longitude de ce lieu repéré sur la carte ci-dessous.

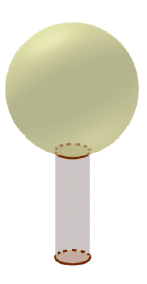
2. On considère que ce globe est composé d’un cylindre en cristal de
diamètre 6 cm, surmonté d’une boule de cristal. Voir schéma ci-dessous.

Montrer qu’une valeur approchée du volume de la boule de ce trophée est de 6371 .
3. Marie affirme que le volume de la boule de cristal représente environ 90% du volume total du trophée. A-t-elle raison ?

Rappels :

– volume d’une boule de rayon R : $V=\frac{4}{3}\pi\times \,R^3$

– volume d’un cylindre de rayon r et de hauteur h : $V=\pi\times ,r^2\times ,h$

Exercice 2 (14 points)
Parmi les nombreux polluants de l’air, les particules fines sont régulièrement surveillées.
Les PM10 sont des particules fines dont le diamètre est inférieur à 0,01 mm.
En janvier 2017, les villes de Lyon et Grenoble ont connu un épisode de pollution aux particules fines. Voici des données concernant la période du 16 au 25 janvier 2017 :

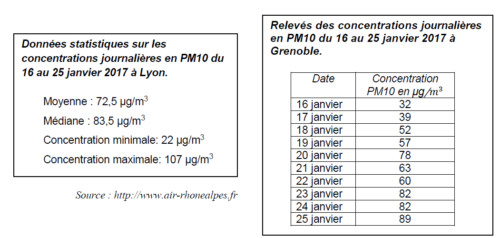
1. Laquelle de ces deux villes a eu la plus forte concentration moyenne en PM10 entre le 16 et le 25 janvier ?
2. Calculer l’étendue des séries des relevés en PM10 à Lyon et à Grenoble. Laquelle de ces deux villes a eu l’étendue la plus importante ? Interpréter ce dernier résultat.
3. L’affirmation suivante est-elle exacte ? Justifier votre réponse.
« Du 16 au 25 janvier, le seuil d’alerte de 80 μg/ par jour a été dépassé au moins 5 fois à Lyon ».

Exercice 3 (12 points)
Dans son lecteur audio, Théo a téléchargé 375 morceaux de musique. Parmi eux, il y a 125 morceaux de rap. Il appuie sur la touche « lecture aléatoire » qui lui permet d’écouter un morceau choisi au hasard parmi tous les morceaux disponibles.

1. Quelle est la probabilité qu’il écoute du rap ?
2. La probabilité qu’il écoute du rock est égale à $\frac{7}{15}$ .
Combien Théo a-t-il de morceaux de rock dans son lecteur audio ?

3. Alice possède 40 % de morceaux de rock dans son lecteur audio.
Si Théo et Alice appuient tous les deux sur la touche « lecture aléatoire » de leur lecteur audio, lequel a le plus de chances d’écouter un morceau de rock ?

Exercice 4 (14 points)
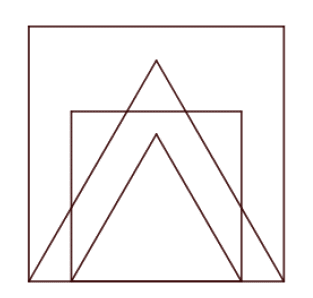
La figure ci-dessous n’est pas représentée en vraie grandeur.
Les points , et sont alignés.
Le triangle est rectangle en .
Le triangle est rectangle en .

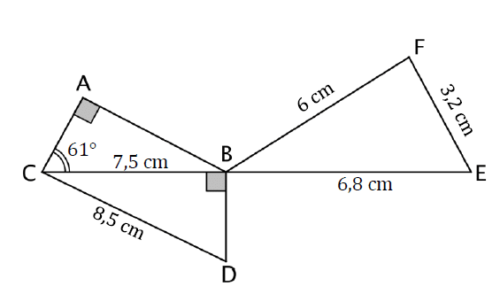
1. Montrer que la longueur est égale à 4 cm.
2. Montrer que les triangles et sont semblables.
3. Sophie affirme que l’angle $\widehat{BFE}$ est un angle droit. A-t-elle raison ?
4. Max affirme que l’angle $\widehat{ACD}$ est un angle droit. A-t-il raison ?

Exercice 5 (16 points)
Voici un programme de calcul.

1. Vérifier que si on choisit le nombre −1, ce programme donne 8 comme résultat final.
2. Le programme donne 30 comme résultat final, quel est le nombre choisi au départ ?
Dans la suite de l’exercice, on nomme le nombre choisi au départ.
3. L’expression donne le résultat du programme de calcul précédent pour un nombre x donné.
On pose .
Prouver que les expressions et B sont égales pour toutes les valeurs de .
4. Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse. On rappelle que les réponses doivent être justifiées.

Affirmation 1 : Ce programme donne un résultat positif pour toutes les valeurs de .
Affirmation 2 : Si le nombre choisi est un nombre entier, le résultat obtenu est un multiple de 8.

Exercice 6 (16 points)
Les longueurs sont en pixels.
L’expression « s’orienter à 90 » signifie que l’on s’oriente vers la droite.

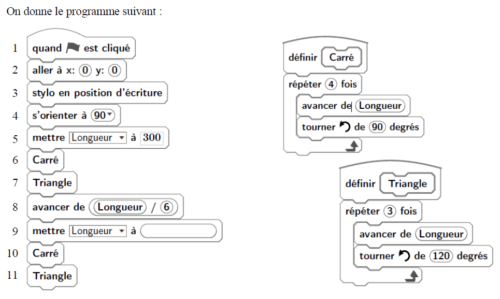
1. On prend comme échelle 1 cm pour 50 pixels.
a. Représenter sur votre copie la figure obtenue si le programme est exécuté jusqu’à la ligne 7 comprise.
b. Quelles sont les coordonnées du stylo après l’exécution de la ligne 8 ?
2. On exécute le programme complet et on obtient la figure ci-dessous qui possède un axe de symétrie vertical.

Recopier et compléter la ligne 9 du programme pour obtenir cette figure.
3. a. Parmi les transformations suivantes, translation, homothétie, rotation, symétrie axiale, quelle est la transformation géométrique qui permet d’obtenir le petit carré à partir du grand carré ? Préciser le rapport de réduction.
b. Quel est le rapport des aires entre les deux carrés dessinés ?

Exercice 7 (17 points)
Le hand-spinner est une sorte de toupie plate qui tourne sur elle-même.

On donne au hand-spinner une vitesse de rotation initiale au temps t = 0, puis, au cours du temps, sa vitesse de rotation diminue jusqu’à l’arrêt complet du hand-spinner. Sa vitesse de rotation est alors égale à 0.
Grâce à un appareil de mesure, on a relevé la vitesse de rotation exprimée en nombre de tours par seconde.
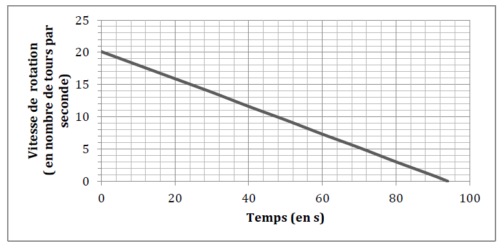
Sur le graphique ci-dessous, on a représenté cette vitesse en fonction du temps exprimé en seconde :

1. Le temps et la vitesse de rotation du hand-spinner sont-ils proportionnels ? Justifier.
2. Par lecture graphique, répondre aux questions suivantes :
a. Quelle est la vitesse de rotation initiale du hand-spinner (en nombre de tours par seconde) ?
b. Quelle est la vitesse de rotation du hand-spinner (en nombre de tours par seconde) au bout d’1 minute et 20 secondes ?
c. Au bout de combien de temps, le hand-spinner va-t-il s’arrêter ?
3. Pour calculer la vitesse de rotation du hand-spinner en fonction du temps , notée (), on utilise la fonction suivante :
$V(t)=-0,214\times ,t+V_{initiale}$
t est le temps (exprimé en s) qui s’est écoulé depuis le début de rotation du hand-spinner
$V_{initiale}$ est la vitesse de rotation à laquelle on a lancé le hand-spinner au départ.

a. On lance le hand-spinner à une vitesse initiale de 20 tours par seconde.

Sa vitesse de rotation est donc donnée par la formule : $V(t)=-0,214\times ,t+20$ .

Calculer sa vitesse de rotation au bout de 30 s.
b. Au bout de combien de temps le hand-spinner va-t-il s’arrêter ? Justifier par un calcul.
c. Est-il vrai que, d’une manière générale, si l’on fait tourner le hand-spinner deux fois plus vite au départ, il tournera deux fois plus longtemps ? Justifier.

Consulter le corrigé en ligne

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «sujet 2018 France du brevet de maths des collèges» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres utilitaires pour progresser en autonomie :

Chronomètre Horloge France Tables Multiplication Arrondir des décimaux Rapporteur et Angles Médiatrice Symétrie Axiale d'un triangle Symétrie Centrale d'un triangle Translation d'un triangle Rotation Homothétie Bissectrice Tracer droite parallèle Conversion Aires et Volumes Addition de deux relatifs Soustraction Relatifs Addition et soustraction de trois relatifs Produit Deux Relatifs Produit Trois Relatifs Quotient Relatifs Carré Entier Racine Carrée Théorème Pythagore Liste Diviseurs Décomposition Facteurs Premiers Calcul du PGCD PGCD Algorithme Euclide Test Nombre Premier Déterminer Fonction Linéaire Déterminer Fonction Affine Traceur Courbe Trigonométrie Angle Trigonométrie Longueur Périmètre d'un Cercle Aire d'un Disque Volume du Parallélépipède Rectangle Volume du cylindre Surface d'une Sphère et Volume d'une boule Volume d'une pyramide à base rectangulaire Section d'une pyramide Visualiser Section Cône en 2D Section d'un Cône Carte Mondiale Coordonnées Géographiques

Mathovore c'est 14 081 150 cours et exercices de maths téléchargés en PDF.