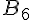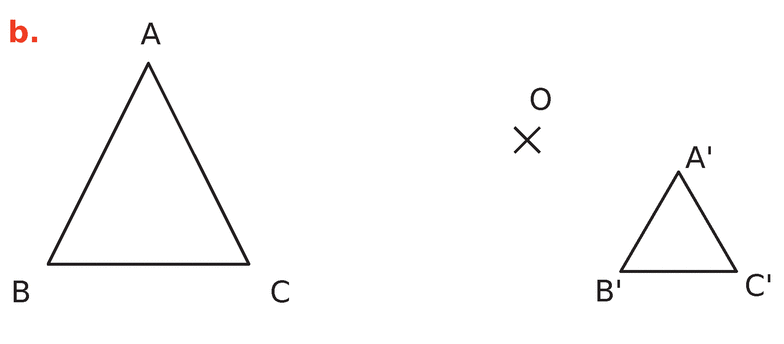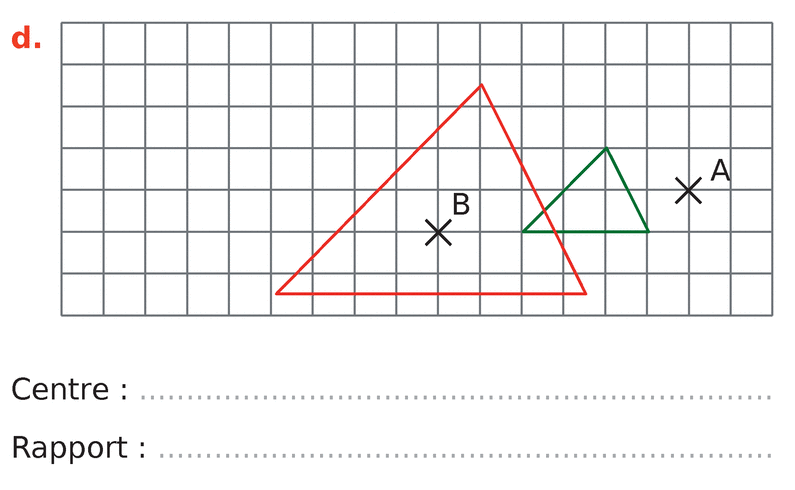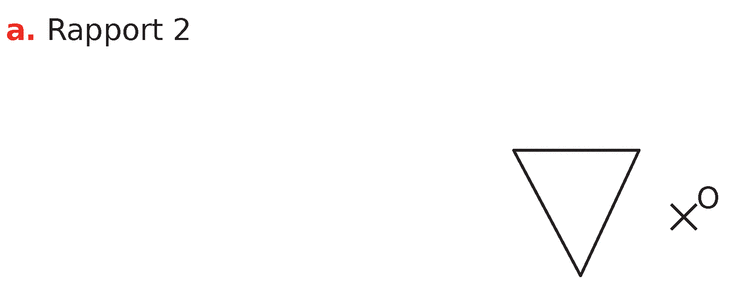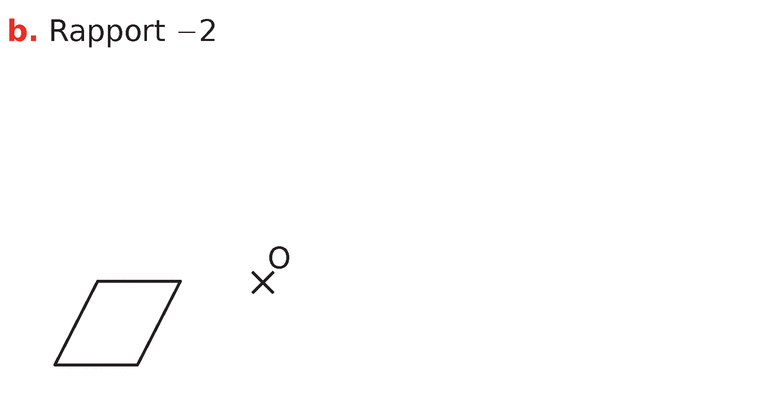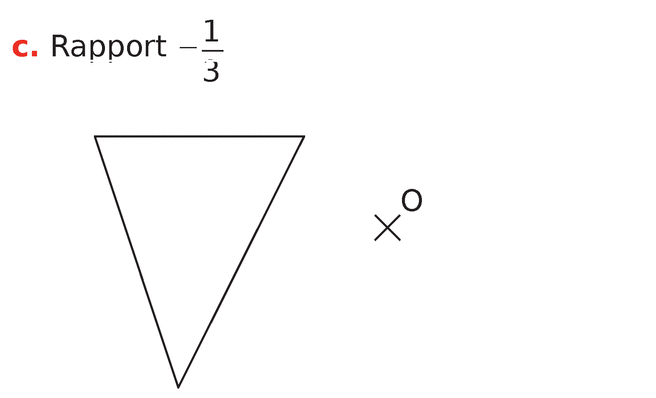Homothéties : exercices de maths en 3ème corrigés en PDF.

Mis à jour le 28 mai 2025

Sommaire

✏️Exercices

3ème • Collège

Homothéties

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Collège

📱 Format : Gratuit

📄 PDF : Disponible

Les homothéties à travers des exercices de maths en 3ème corrigés faisant intervenir des constructions et l’utilisation des propriétés de l’homothétie. L’élève devra être capable de construire l’image d’une figure par une homothétie de centre O et de rapport k et d’effectuer des démonstrations en utilisant ses différentes propriétés.

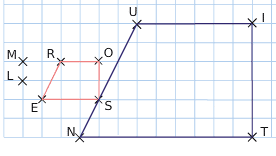
Exercice 1

Par quelle homothétie…

le quadrilatère NUIT est-il l’image du quadrilatère ROSE ?
le quadrilatère ROSE est-il l’image du quadrilatère NUIT ?

Exercice 2 :

Le quadrilatère orange ci-dessous est l’image du quadrilatère rose

par l’homothétie de centre O et de rapport 3.

Si le périmètre du rectangle rose est de 8 cm, quel est celui du rectangle orange ?
Si l’aire du rectangle orange est de 72 cm², quelle est celle du rectangle rose ?

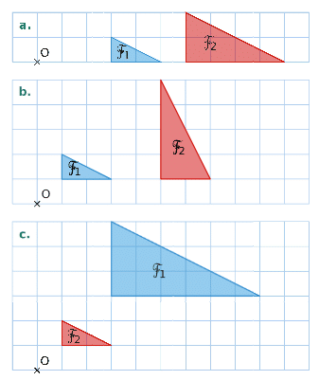
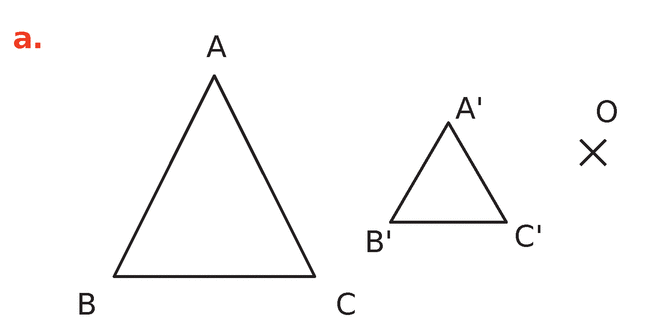
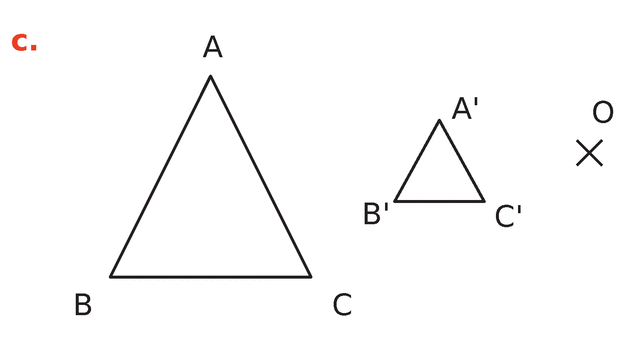
Exercice 3 :

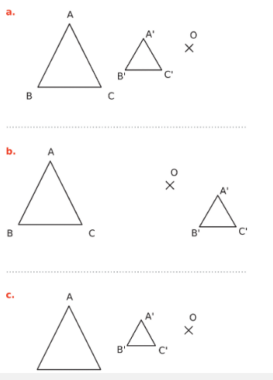
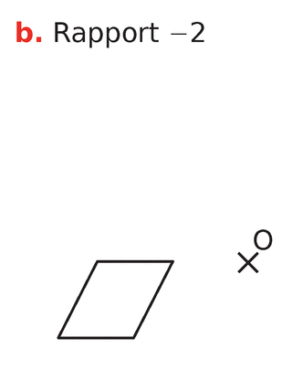
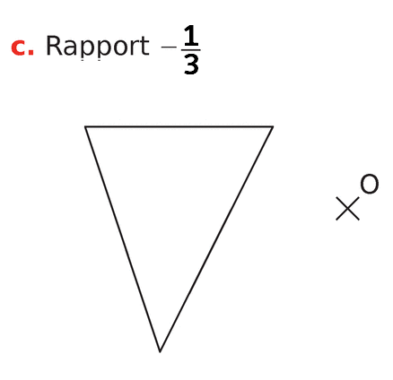
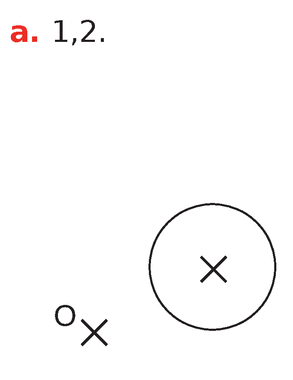
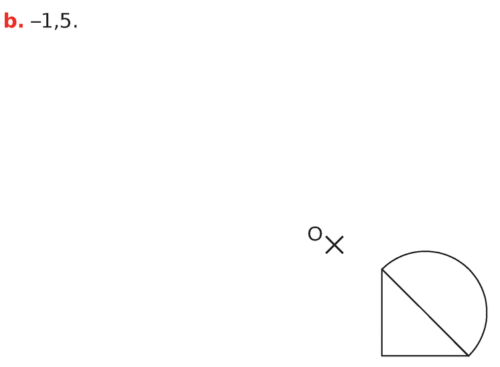
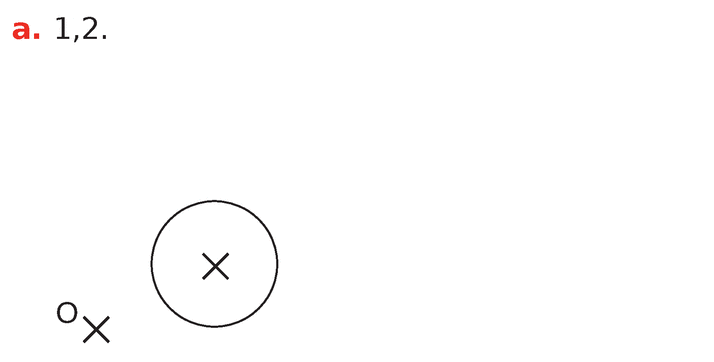
Dans les cas ci-dessous, indiquer si la figure est l’image de la figure par une homothétie de centre O.

Si c’est le cas, préciser son rapport.

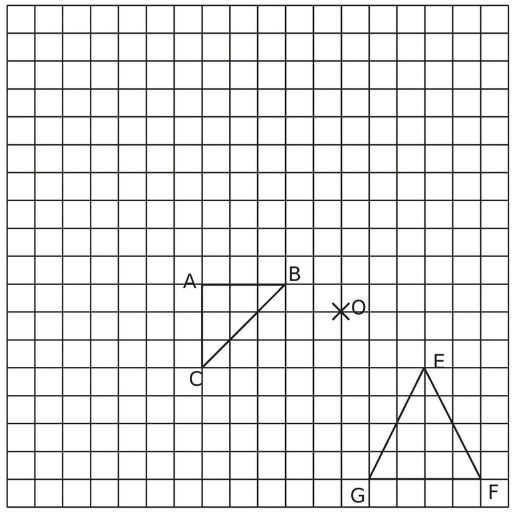
Exercice 4 :

Préciser la transformation qui transforme la figure en la figure …

1. 2. 3. 4. 5.

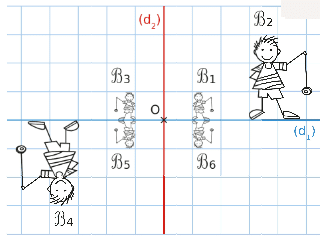
Exercice 5 :

Construire l’image L’M’N’P’ de ce quadrilatère par l’homothétie de centre O

et de rapport 2.

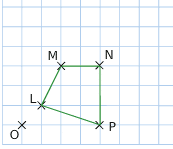
Exercice 6 :

Sur la figure suivante, ABC est un triangle rectangle en A tel que AB= 6 cm et AC= 8 cm.

A’B’C’ est l’image de ABC par une homothétie de centre O.

1.Donner en justifiant, le rapport de cette homothétie.

2.Quelle est la nature du triangle A’B’C’ ?

3. Calculer le périmètre puis l’aire du triangle ABC.

4. En déduire le périmètre puis l’aire du triangle A’B’C’.

Exercice 7 :

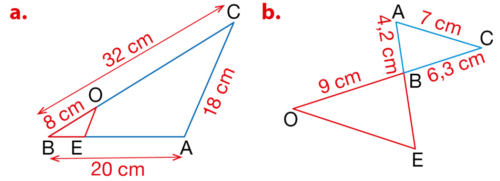
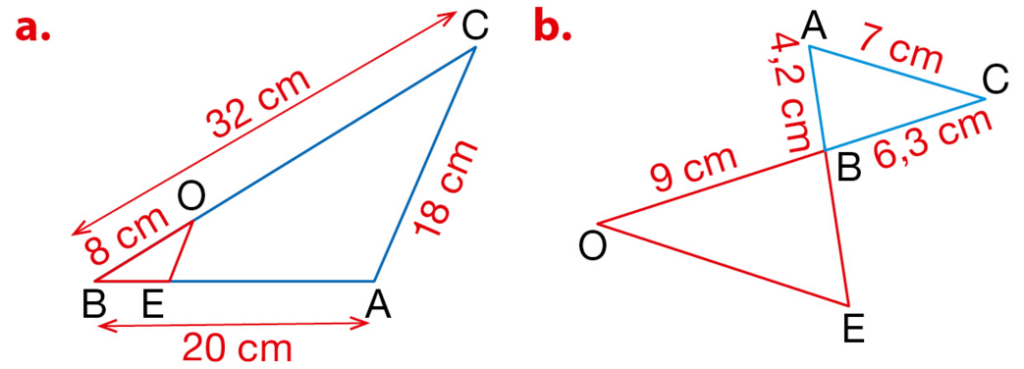
Dans chaque cas, on passe du triangle OBE au triangle ABC par une homothétie.
Donner le centre et le rapport de l’homothétie, puis calculer les longueurs OE et BE.

Exercice 8 :

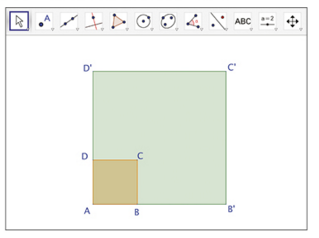
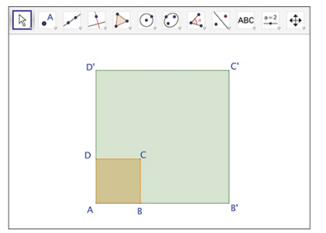
a. Avec un logiciel de géométrie, construire un carré ABCD de côté 2 cm.
b. Construire l’image de ce carré par l’homothétie de centre A et de rapport 3.
Noter B’, C’, D’ les images respectives de B, C, D.
Quelle est la nature de AB’C’D ?
Quelle est la longueur de son côté ?

c. Construire l’image de ABCD par l’homothétie de centre A et de rapport 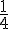$\frac{1}{4}$ .
Noter B », C », D » les images respectives de B, C, D.
Quelle est la nature de AB »C »D » ?
Quelle est la longueur de son côté ?
d. Construire l’image de ABCD par l’homothétie de centre A et de rapport 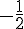$-\frac{1}{2}$ .
Noter , , les images respectives de B, C, D.
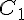
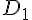
Quelle est la nature de A?
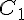
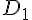
Quelle est la longueur de son côté ?
e. Tracer les droites (AB), (AC), (AD). Que constate-t-on ?

Exercice 9 :

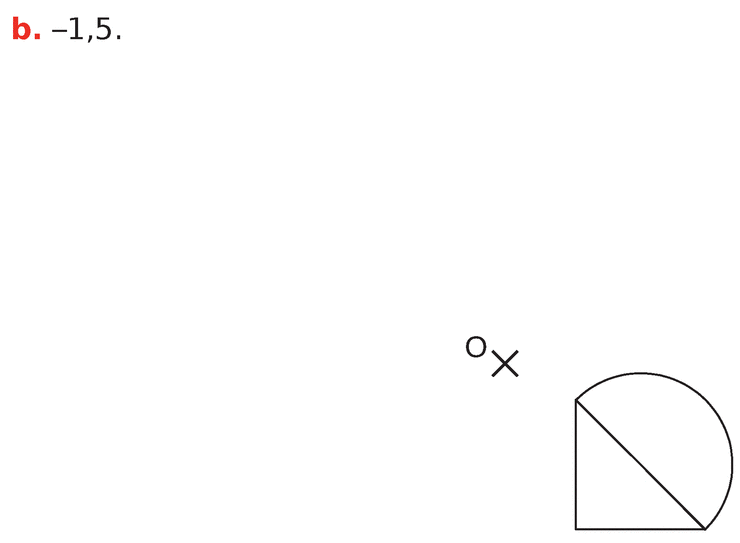
a. Construire un cercle 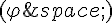$(\varphi\,)$ de centre O et de rayon 2 cm.
b. Par une homothétie, l’image d’un cercle est un cercle.
Construire l’image du cercle 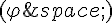$(\varphi\,)$ par l’homothétie de centre O et de :
• rapport 1,5
• rapport 0,75
• rapport -2.

Exercice 10 :

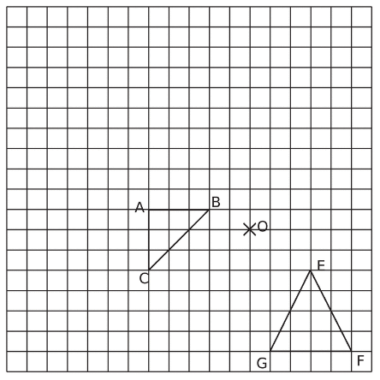
Dans chacun des cas suivants, dis si A’B’C’ est l’image du triangle ABC par une homothétie de
centre O.

Exercice 11 :

a. Construire A’B’C’, l’image par l’homothétie de centre O et de rapport 2 du triangle ABC
b. Construire E’F’G’, l’image par l’homothétie de centre O et de rapport – 1,5 du triangle EFG.

Exercice 12 :

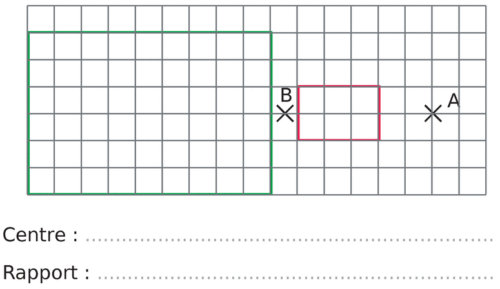
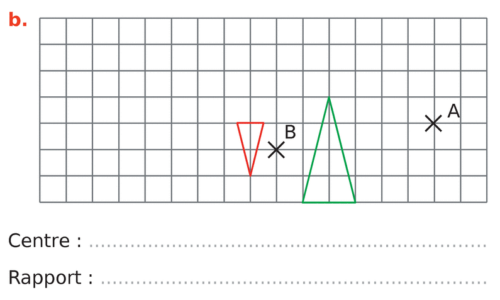
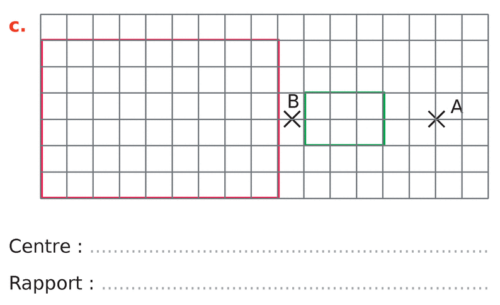
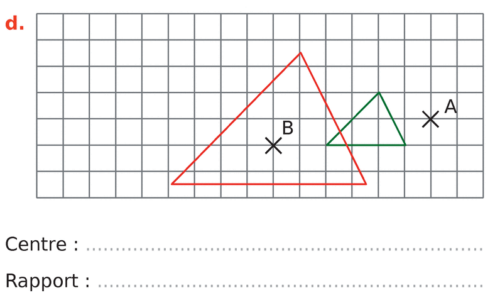
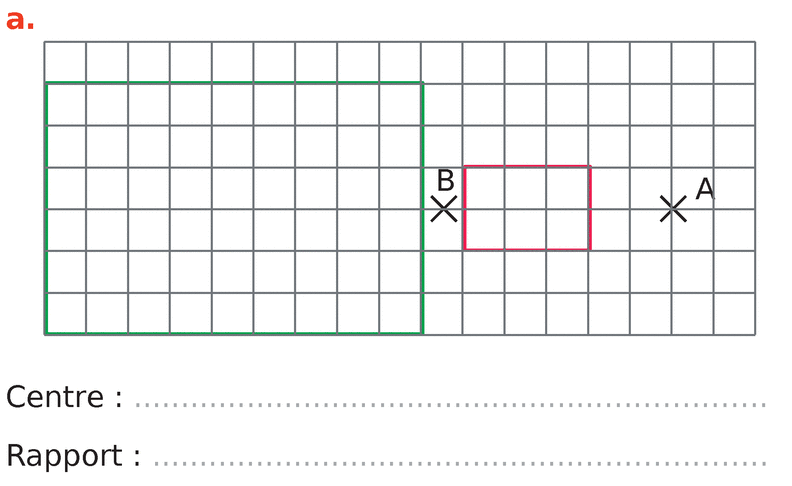
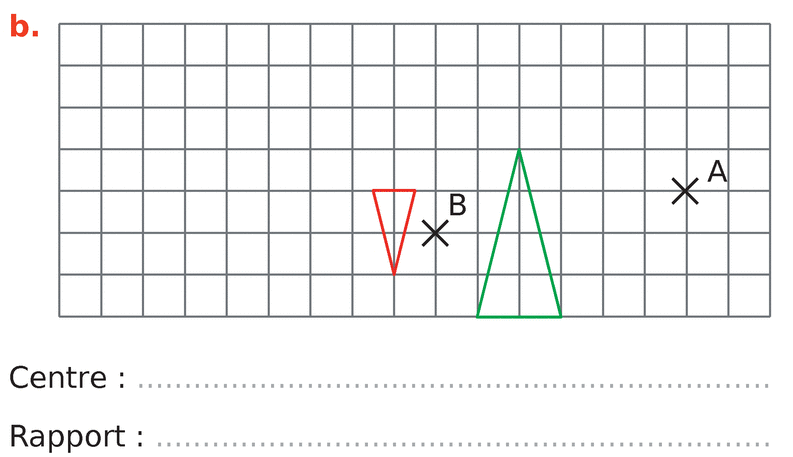
Dans chacun des cas suivants, la figure verte est l’image de la figure rouge par une homothétie.
Déterminer son centre et son rapport.

Exercice 13 :

Dans chaque cas, construis l’image de la figure proposée par l’homothétie de centre O et de rapport
indiqué.

Exercice 14 :

Dans chaque cas, construis l’image de la figure dans l’homothétie de centre O et de rapport :

Exercice 15 :

L’homothétie de centre I et de rapport transforme un segment [AB] en un segment [A’B’].
a. Construire cette figure.
b. Que peut-on dire des droites (AB) et (A’B’) ?
Justifier.

Exercice 16 :
Dans chacun des cas suivants, dire si A’B’C’ est l’image du triangle ABC par une homothétie de
centre O.

Exercice 17 :

a. Construire A’B’C’, l’image par l’homothétie de centre O et de rapport 2 du triangle ABC
b. Construire E’F’G’, l’image par l’homothétie de centre O et de rapport 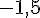du triangle EFG.

Exercice 18 :

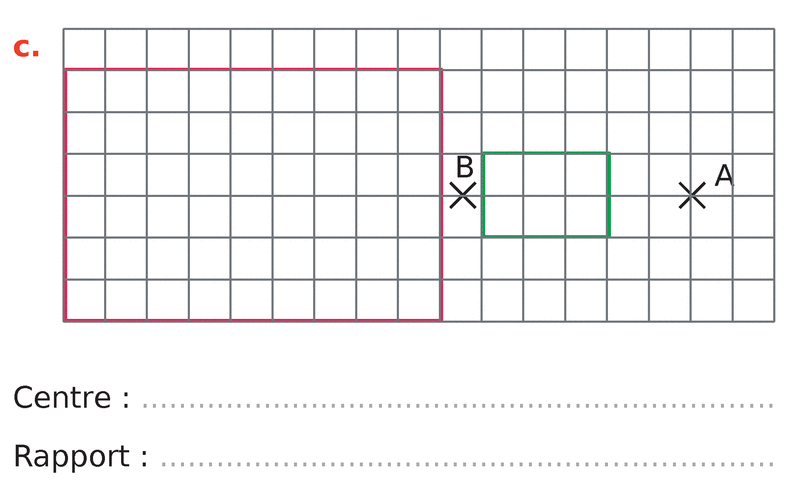
Dans chacun des cas suivants, la figure verte est l’image de la figure rouge par une homothétie.
Déterminer son centre et son rapport.

Exercice 19 :

Dans chaque cas, construire l’image de la figure proposée par l’homothétie de centre O et de rapport
indiqué.

Exercice 20 :

Dans chaque cas, construire l’image de la figure dans l’homothétie de centre O et de rapport :

Exercice 21 :

L’homothétie de centre I et de rapport transforme un segment [AB] en un segment [A’B’].
a. Construire cette figure.
b. Que peut-on dire des droites (AB) et (A’B’) ?
Justifier.

Exercice 22 :

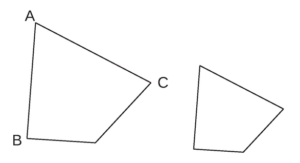
Les deux quadrilatères ci-dessous sont homothétiques.
a. Coder sur la figure les angles de même mesure.
b. Si AB = AC, coder sur la figure deux autres longueurs égales.
c. Repasser en rouge deux segments parallèles.

Exercice 23 :

Un triangle A’B’C’ est l’image d’un triangle ABC dans une homothétie de rapport 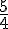$\frac{5}{4}$ .

On sait que AB = 6 cm et que l’angle 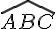$\widehat{ABC}$ mesure 60°.
Détermine les mesures de leurs images A’B’ et 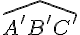$\widehat{A'B'C'}$ . Justifier.

Exercice 24 :
RULP est un trapèze rectangle. OKFM est son image par une homothétie de rapport 0,5.
a. Construire le centre I de cette homothétie.

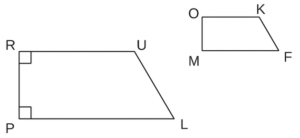
b. Quelle est la nature du quadrilatère OKFM ? Justifier.

Exercice 25 :

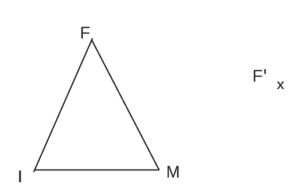
Terminer la construction de l’image du triangle FMI par une homothétie de rapport 0,5.

Exercice 26 :

Le carré EFGH est l’image du carré ABCD dans une homothétie de rapport 5.

On suppose que le côté du carré ABCD mesure 3 cm.

a. Calculer la mesure du côté de EFGH et en déduire son aire.

b. Compléter : Aire EFGH Aire ABCD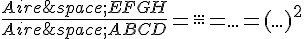 $\frac{Aire\,EFGH}{Aire\,ABCD}=\frac{...}{...}=...=(...)^2$ .

Exercice 27 :

L’aire d’un pentagone est 24 cm².

Quelle sera l’aire de son image par une homothétie de rapport :
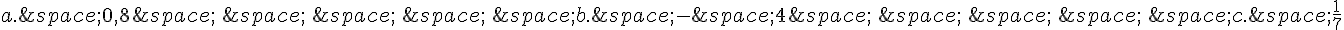
$a.\,0,8\,\,\,\,\,\,\,\,\,b.\,-\,4\,\,\,\,\,\,\,\,\,c.\,\frac{1}{7}$

Exercice 28 :

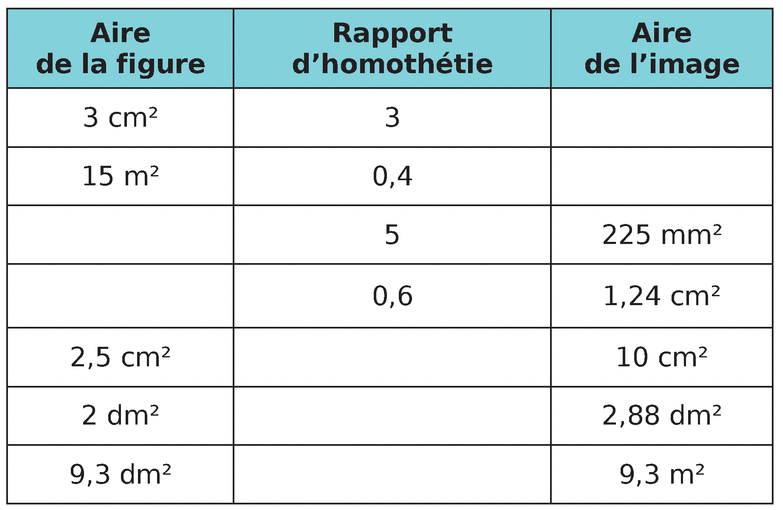
Compléter le tableau.

Exercice 29 :

Dans chaque cas, on passe du triangle OBE au triangle ABC par une homothétie.
Donner le centre et le rapport de l’homothétie, puis calculer les longueurs OE et BE.

Exercice 30 :

c. Construire l’image de ABCD par l’homothétie de centre A et de rapport 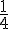$\frac{1}{4}$ .
Noter B », C », D » les images respectives de B, C, D.
Quelle est la nature de AB »C »D » ?
Quelle est la longueur de son côté ?
d. Construire l’image de ABCD par l’homothétie de centre A et de rapport 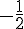$-\frac{1}{2}$ .
Noter 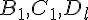les images respectives de B, C, D.
Quelle est la nature de AB »C »D » ?
Quelle est la longueur de son côté ?
e. Tracer les droites (AB), (AC), (AD). Que constate-t-on ?

Exercice 31 :

a. Construire un cercle 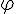$\varphi$ de centre O et de rayon 2 cm.
b. Par une homothétie, l’image d’un cercle est un cercle.
Construire l’image du cercle 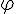$\varphi$ par l’homothétie de centre O et de :

rapport 1,5
rapport 0,75
rapport -2.

4.6/5 - (26927 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «homothéties : exercices de maths en 3ème corrigés en PDF.» au format PDF.

Ressources de troisième

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Homothéties : exercices de maths en 3ème corrigés en PDF.

L’équipe Mathovore

12 Enseignants Titulaires

Ressources de troisième

Cours de troisième

Exercices de troisième

Brevet