Centres étrangers 2025 : brevet de maths avec sujet et corrigé en PDF.
Mis à jour le 27 septembre 2025
DIPLÔME NATIONAL DU BREVET
SESSION 2025
CENTRES ETRANGERS
MATHÉMATIQUES
Série générale
Durée de l’épreuve: 2 h 00
100 points
Exercice 1 (20 points)
Cet exercice est un questionnaire à choix multiple (QCМ).
Pou chaque question, quatre réponses sont proposées.
Une seule réponse est exacte.
Recopier sur la copie le numéro de la question et la réponse choisie.
Aucune justification n’est demandée.
Question 1
La décomposition en produit de facteurs premiers de 120 est :

Question 2
Dans la cellule A2, la formule « = − 4 * А1 – 12 » a été saisie.

On l’étire jusqu’à la cellule B2.
La valeur obtenue dans la cellule B2 est :

Question 3
Sur la figure ci-dessous, le rapport de l’homothétie de centre O qui transforme le carré A en le carré B est :
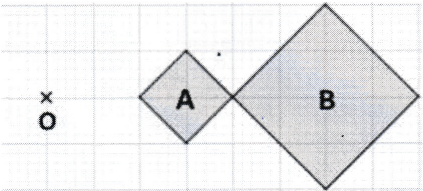

Question 4
Une écriture factorisée de 4x² – 1 est:

Question 5
Dans le triangle TER ci-contre, la mesure de la longueur RE arrondie au centième de cm est :
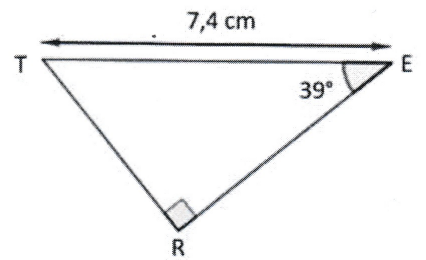

Exercice 2 (19 points)
L’entreprise < Transport Rapide » doit livrer cinq colis nommés A, B, C, D et E ayant des masses différentes précisées dans le tableau ci-dessous :

1. Calculer la moyenne des masses des colis en kg.
2. Déterminer la médiane des masses des colis en kg. Interpréter ce résultat.
3. Le transporteur choisit au hasard un colis parmi les cinq (A, B, C, D ou E) pour une livraison express.
Calculer la probabilité pour qu’il sélectionne un colis dont la masse est inférieure à 8 kg.
Les colis ont la forme d’un pavé droit de longueur L, de largeur l et de hauteur h, représenté ci-dessous.
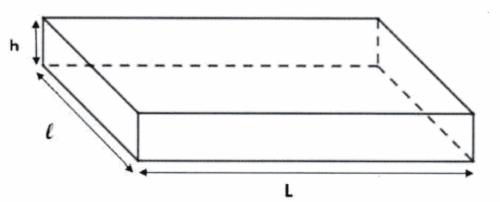
Voici les dimensions des cinq colis.
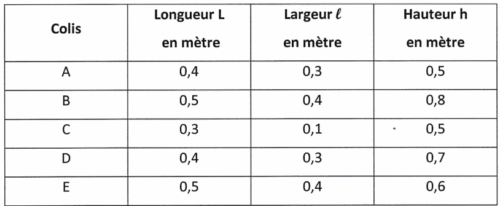
4. a. Vérifier que le volume du colis E est de 0,12 m³.
b. L’entreprise souhaite calculer la masse volumique d’un colis dont la formule est rappelée
ci-dessous. Montrer que la masse volumique du colis E arrondie au dixième est 91,7 kg/m³.

c. Le transporteur affirme « Le colis E est plus lourd que le colis C, donc la masse volumique du colis E
est plus grande que celle du colis C. » A-t-il raison?
Exercice 3 (21 points)
On considère le programme de calcul suivant.

1. Montrer que si l’on choisit 1 comme nombre de départ dans le programme, le résultat obtenu est 8.
2. Quel est le résultat si le nombre de départ est -2?
3. Si l’on note x le nombre de départ, montrer que le résultat peut s’écrire -8x + 16.
4. a. Résoudre l’équation -8x +16 = 4.
b. En déduire le nombre de départ qu’il faut choisir pour obtenir 4 comme résultat.
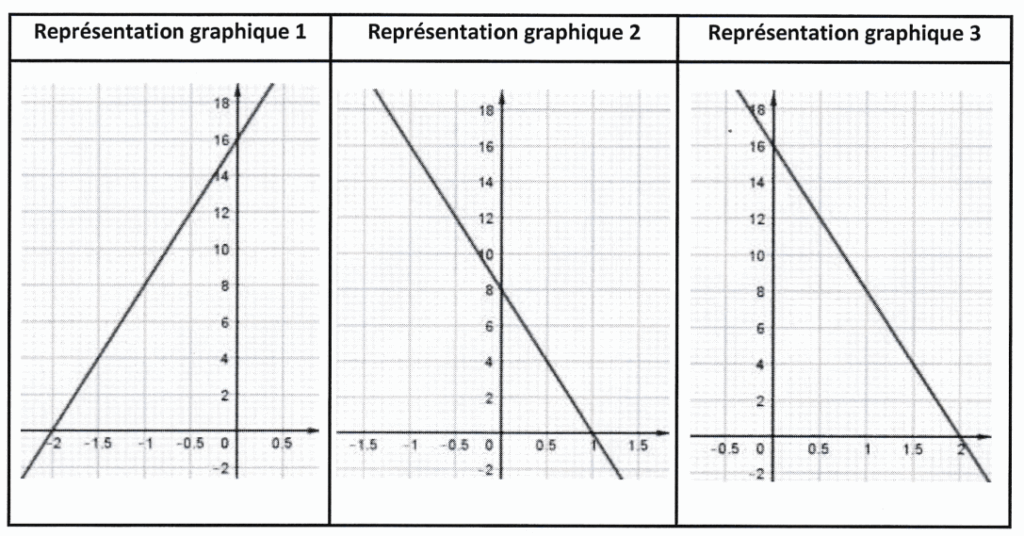
5. Parmi les trois représentations graphiques ci-dessous, quelle est celle qui représente la
fonction f définie par f(x) = -8x + 16 ? Expliquer la démarche.
Exercice 4 (21 points)
Un agriculteur souhaite cultiver un champ représenté par le triangle ABC ci-dessous.
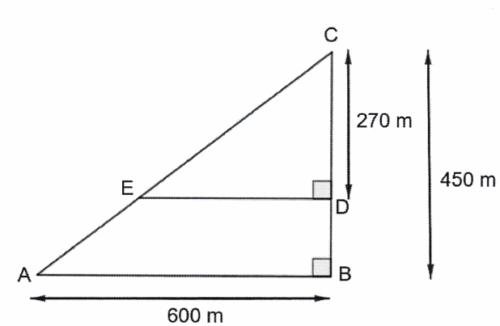
Sur la figure qui n’est pas à l’échelle, on a les informations suivantes:
- le triangle ABC est rectangle en B
- les points C, E et A sont alignés;
- les points C, D et B sont alignés;
- AB = 600 m; BC = 450 m; CD = 270 m.
Les parties A et B sont indépendantes.
Partie A: étude géométrique du terrain
1. Montrer que le segment [AC] mesure 750 mètres.
2. a. Montrer que les droites (ED) et (AB) sont parallèles.
b. Montrer que le segment [DE] mesure 360 mètres.
3. Montrer que l’aire du triangle CDE est 48 600 m².
Partie B: étude du prix du mélange de graines
L’agriculteur souhaite semer un mélange de graines (blé, seigle et pois) en respectant les indications suivantes.
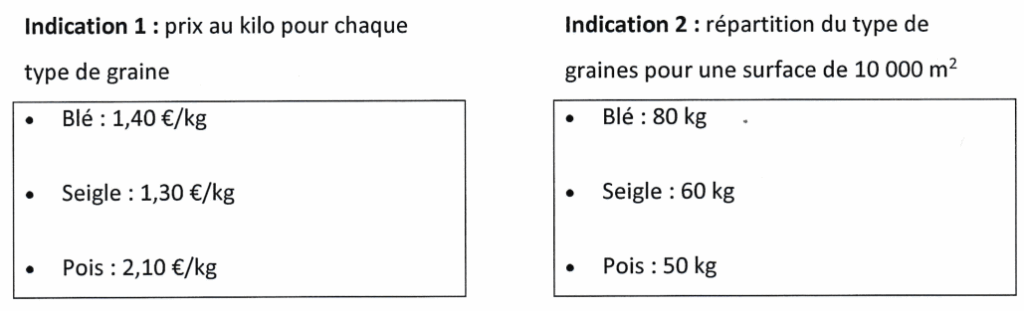
1. Un vendeur lui propose des sacs contenant un mélange de blé, seigle, et pois selon le ratio
16: 12:8.
Montrer que la composition de ce sac ne respecte pas l’indication 2.
2. L’agriculteur souhaite semer le mélange de graines sur la partie du champ représentée par le
triangle CDE dont l’aire mesure 48 600 m². II a calculé qu’il doit prévoir 388,80 kg de blé pour
respecter la répartition indiquée dans l’énoncé. Justifier le calcul de l’agriculteur.
3. L’agriculteur dispose d’un budget de 1 500 € pour semer le mélange de graines sur la totalité des 48 600 m² de terrain.
Il a calculé qu’il doit acheter 388,80 kg de blé, 291,6 kg de seigle et 243 kg de pois pour respecter la répartition indiquée dans l’énoncé.
L’agriculteur dispose-t-il d’un budget suffisant ?
Exercice 5 (19 points)
Un digicode commande l’ouverture de la porte d’entrée de la maison de la grand-mère de Léna.
Léna a oublié le code. Elle sait qu’il est composé d’une lettre A, B, ou C, suivie d’un chiffre compris entre 0 et 9.
1. Proposer deux codes différents que Léna peut tester.
2. Quelle est la probabilité que la grand-mère de Léna ait choisi la lettre C dans son code?
3. Montrer que la probabilité que la grand-mère de Léna ait choisi le chiffre 7 dans son code est 1/10.
4. Léna se souvient que sa grand-mère, enseignante de mathématiques à la retraite, aime bien les nombres premiers.
Quelle est la probabilité que le code choisi par sa grand-mère comporte un nombre premier ?
5. a. Léna décide de tester tous les codes possibles.
Elle estime qu’il lui faut 5 secondes pour essayer un code.
Réussira-t-elle à ouvrir la porte de la maison en moins de 3 minutes?
b. Le format de ce code garantit-il la sécurité de la maison?
Comment pourrait-on améliorer ce système de code?
Chaque fois qu’un utilisateur saisit un code, un programme lui annonce si le code est correct ou faux.
Le programme utilisé est noté ci-dessous.
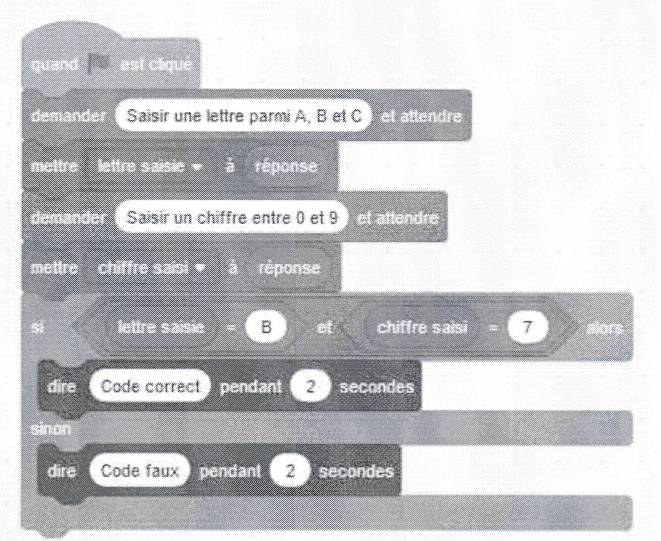
a. Léna saisit le code B5. Qu’affiche le programme?
b. D’après ce programme, quel est le code qui permet d’entrer dans l’immeuble de la grand-mère de Léna ?
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «centres étrangers 2025 : brevet de maths avec sujet et corrigé en PDF.» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.











