L’essentiel : Sujet complet du brevet de maths 2017 0, 7 exercices, à faire en conditions d’examen. Le corrigé détaillé est sur une page séparée ; sujet gratuit à télécharger en PDF.
Nouveau sujet de la nouvelle épreuve de mathématiques pour la session 2017 suite à la réforme du collège. Voici le sujet zéro du brevet de maths 2017 pour vous entraîner.
Ainsi, ce sujet officiel est tiré du site Eduscol.
Exercice 1 – sujet zéro du brevet 2017
Pour chacune des affirmations suivantes, dire si elle est vraie ou fausse en justifiant soigneusement la réponse.
1) Un sac contient 6 jetons rouges, 2 jetons jaunes et des jetons verts.
Ensuite, la probabilité de tirer un jeton vert vaut 0,5.
Affirmation : le sac contient 4 jetons verts.
2) En informatique, on utilise comme unités de mesure les multiples suivants de l’octet :
, 
, 
, 
,
où Ko est l’abréviation de kilooctet, Mo celle de mégaoctet, Go celle de gigaoctet, To celle de téraoctet.
Ensuite, on partage un disque dur de 1,5 To en dossiers de 60 Go chacun.
Affirmation : on obtient ainsi 25 dossiers.
3) Sur la figure codée ci-dessous, les points B, A et E sont alignés.
Affirmation : l’angle 
mesure 137°.
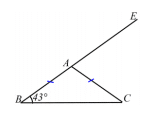
4) Un verre de forme conique est complètement rempli.
Par ailleurs, on verse son contenu de sorte que la hauteur du liquide soit divisée par 2.
Affirmation : le volume du liquide est divisé par 6.
Exercice 2 – sujet zéro du brevet 2017
Le marnage désigne la différence de hauteur entre la basse mer et la pleine mer qui suit.
Puis on considère qu’à partir du moment où la mer est basse, celle-ci monte de 1/12 du marnage pendant la première heure, de 2/12 pendant la deuxième heure, de 3/12 pendant la troisième heure, de 3/12 pendant la quatrième heure, de 2/12 pendant la cinquième heure et de 1/12 pendant la sixième heure. De même, au cours de chacune de ces heures, la montée de la mer est supposée régulière.
1) À quel moment la montée de la mer atteint-elle le quart du marnage ?
2) À quel moment la montée de la mer atteint-elle le tiers du marnage ?
Exercice 3
Pour la fête d’un village on organise une course cycliste. En outre, une prime totale de 320 euros sera répartie entre les trois premiers coureurs.
Également, le premier touchera 70 euros de plus que le deuxième et le troisième touchera 80 euros de moins que le deuxième.
Ainsi, déterminer la prime de chacun des trois premiers coureurs.
Exercice 4
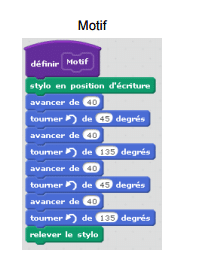
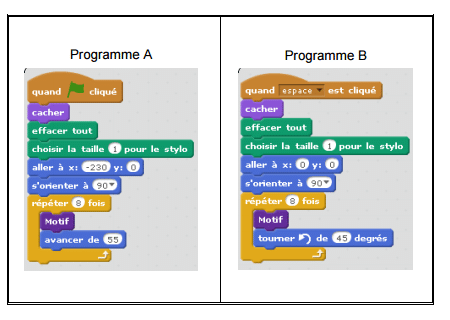
1) Pour réaliser la figure ci-dessus, on a défini un motif en forme de losange et on a utilisé l’un des deux programmes A et B ci-dessous.
Déterminer lequel et indiquer par une figure à main levée le résultat que l’on obtiendrait avec l’autre programme.
2) Combien mesure l’espace entre deux motifs successifs ?
3) On souhaite réaliser la figure ci-dessous :
Pour ce faire, on envisage d’insérer l’instruction
Où faut-il insérer cette instruction ?
Exercice 5
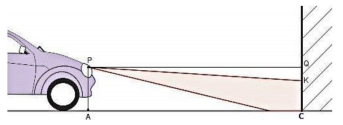
Pour régler les feux de croisement d’une automobile, on la place face à un mur vertical. Ensuite, le phare, identifié au point P, émet un faisceau lumineux dirigé vers le sol.
Par ailleurs, on relève les mesures suivantes :
PA = 0,7 m, AC = QP = 5 m et CK = 0,61 m.
De même, sur le schéma ci-contre, qui n’est pas à l’échelle, le point S représente l’endroit où
le rayon supérieur du faisceau rencontrerait le sol en l’absence du mur.
Ensuite, on considère que les feux de croisement sont bien réglés si le rapport 
est compris entre 0,015 et 0,02.
1) Vérifier que les feux de croisement de la voiture sont bien réglés.
2) À quelle distance maximale de la voiture un obstacle se trouvant sur la route est-il éclairé par les feux de croisement ?
Exercice 6
Un panneau mural a pour dimensions 240 cm et 360 cm. En outre, on souhaite le recouvrir avec des carreaux de forme carrée, tous de même taille, posés bord à bord sans jointure.
1) Peut-on utiliser des carreaux de : 10 cm de côté ? 14 cm de côté ? 18 cm de côté ?
2) Quelles sont toutes les tailles possibles de carreaux comprises entre 10 et 20 cm ?
3) On choisit des carreaux de 15 cm de côté. Également, on pose une rangée de carreaux bleus sur le pourtour et des carreaux blancs ailleurs.
Ainsi, Combien de carreaux bleus va-t-on utiliser ?
Exercice 7
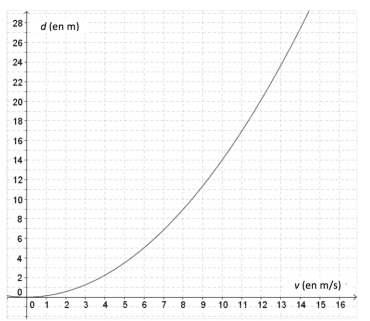
La distance de freinage d’un véhicule est la distance parcourue par celui-ci entre le moment où le conducteur commence à freiner et celui où le véhicule s’arrête. Celle-ci dépend de la vitesse du véhicule. Ensuite, la courbe ci-dessous donne la distance de freinage d, exprimée en mètres, en fonction de la vitesse v du véhicule, en m/s,sur une route mouillée.
1) Démontrer que 10 m/s = 36 km/h.
2) a. Par ailleurs, d’après ce graphique, la distance de freinage est-elle proportionnelle à la vitesse du véhicule ?
b. Estimer la distance de freinage d’une voiture roulant à la vitesse de 36 km/h.
c. De même, un conducteur, apercevant un obstacle, décide de freiner. Puis on constate qu’il a parcouru 25 mètres entre le moment où il commence à freiner et celui où il s’arrête. En outre, déterminer, avec la précision permise par le graphique, la vitesse à laquelle il roulait en m/s.
3) On admet que la distance de freinage d, en mètres, et la vitesse v, en m/s, sont liées par la relation 
.
a. Retrouver par le calcul le résultat obtenu à la question 2b.
b. Également, un conducteur, apercevant un obstacle, freine ; il lui faut 35 mètres pour s’arrêter.
À quelle vitesse roulait-il ?
Ce que contient ce sujet zéro du brevet de maths 2017
Le sujet zéro du brevet de maths 2017 a été conçu pour présenter la nouvelle forme de l’épreuve de mathématiques, avec une première partie d’automatismes. Parmi les notions du programme de troisième, on retrouve notamment les probabilités, les volumes, les vitesses moyennes, les fonctions et la proportionnalité. Ainsi, Si besoin, un rappel sur la notion de probabilité est disponible dans l’encyclopédie en ligne.
Méthode pour travailler le sujet zéro du brevet de maths 2017
D’abord, imprimez ou affichez l’énoncé et composez en deux heures, comme le jour de l’examen. Puis notez les questions sur lesquelles vous avez hésité, afin de revoir les notions correspondantes. Par ailleurs, d’autres annales sont réunies sur la page des sujets du brevet de maths corrigés, ce qui permet de varier les centres d’examen.
Points de vigilance sur ce sujet zéro du brevet de maths 2017
Voici les pièges les plus courants dans ce type d’exercice :
- Une probabilité est toujours comprise entre 0 et 1 : si votre résultat dépasse 1, c’est donc qu’une erreur s’est glissée dans le décompte des issues. Au besoin, revoyez le cours sur les probabilités.
- Pour les volumes, vérifiez que toutes les longueurs sont dans la même unité avant de calculer, car 1 dm³ vaut 1 L et 1 m³ vaut 1 000 L.
- Pour une vitesse moyenne, utilisez la relation distance = vitesse × durée, en convertissant les durées en heures décimales : par exemple, 1 h 30 min correspond à 1,5 h.
- Avec les fonctions, distinguez bien l’image, lue sur l’axe des ordonnées, et l’antécédent, lu sur l’axe des abscisses.
Méthode de travail
Donc, refais les questions ratées deux ou trois jours plus tard. En effet, note dans un cahier les erreurs qui reviennent d’un sujet à l’autre. Pour cela, révise les théorèmes cités dans ce sujet si un point te manque. De même, entraîne-toi sur un autre sujet de 2017 pour progresser en vitesse de calcul. Également, garde toujours une trace écrite propre de chaque étape de calcul. Donc, relis la consigne une seconde fois avant de rendre ta copie.
Méthode de travail
Pour cela, distingue bien ce qui est demandé et ce qui sert seulement au calcul intermédiaire. De même, commence par lire l’énoncé en entier avant de te lancer dans les calculs. Également, repère d’abord les données utiles de chaque exercice sur ton brouillon. Donc, vérifie l’unité demandée avant de recopier un résultat. En effet, compare ta rédaction avec le corrigé, étape par étape. Pour cela, chronomètre-toi une première fois pour connaître ton rythme réel.
Comment progresser sur ce sujet
Également, refais les questions ratées deux ou trois jours plus tard. Donc, note dans un cahier les erreurs qui reviennent d’un sujet à l’autre. En effet, révise les théorèmes cités dans ce sujet si un point te manque. Pour cela, entraîne-toi sur un autre sujet de 2017 pour progresser en vitesse de calcul. De même, garde toujours une trace écrite propre de chaque étape de calcul. Également, relis la consigne une seconde fois avant de rendre ta copie.
Conseils pour bien travailler brevet
En effet, distingue bien ce qui est demandé et ce qui sert seulement au calcul intermédiaire. Pour cela, commence par lire l’énoncé en entier avant de te lancer dans les calculs. De même, repère d’abord les données utiles de chaque exercice sur ton brouillon. Également, vérifie l’unité demandée avant de recopier un résultat. Donc, compare ta rédaction avec le corrigé, étape par étape. En effet, chronomètre-toi une première fois pour connaître ton rythme réel.
Comment progresser sur ce sujet
De même, refais les questions ratées deux ou trois jours plus tard. Également, note dans un cahier les erreurs qui reviennent d’un sujet à l’autre. Donc, révise les théorèmes cités dans ce sujet si un point te manque. En effet, entraîne-toi sur un autre sujet de 2017 pour progresser en vitesse de calcul. Pour cela, garde toujours une trace écrite propre de chaque étape de calcul. De même, relis la consigne une seconde fois avant de rendre ta copie.
