Le sujet et le corrigé du brevet de maths 2017 en Amérique du nord.
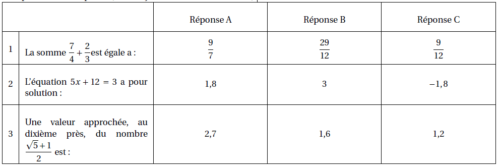
Exercice 1. 4.5 points
Recopier la bonne réponse (aucune justification n’est attendue).
Exercice 2. 9.5 points
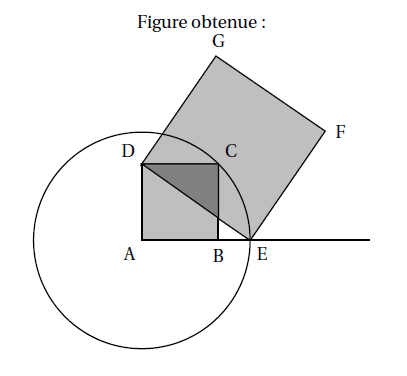
Avec un logiciel de géométrie, on exécute le programme ci-dessous.
Programme de construction :
• Construire un carré ABCD;
• Tracer le cercle de centre A et de rayon [AC] ;
• Placer le point E à l’intersection du cercle et de la
demi-droite [AB) ;
• Construire un carré DEFG.
1. Sur la copie, réaliser la construction avec AB = 3 cm.
2. Dans cette question, AB = 10 cm.
2. a. Montrer que AC =p200 cm.
2. b. Expliquer pourquoi AE =p200 cm.
2. c. Montrer que l’aire du carré DEFG est le triple de l’aire du carré ABCD.
3. On admet pour cette question que pour n’importe quelle longueur du côté [AB], l’aire du carréDEFG est toujours le triple
de l’aire du carré ABCD.
En exécutant ce programme de construction, on souhaite obtenir un carré DEFG ayant une aire de 48 cm2.
Quelle longueur AB faut-il choisir au départ ?
Exercice 3. 6 points
Il y a dans une urne 12 boules indiscernables au toucher, numérotées de 1 à 12. On veut tirer une boule au hasard.
1. Est-il plus probable d’obtenir un numéro pair ou bien un multiple de 3?
2. Quelle est la probabilité d’obtenir un numéro inférieur à 20?
3. On enlève de l’urne toutes les boules dont le numéro est un diviseur de 6. On veut à nouveau tirer une boule au hasard.
Expliquer pourquoi la probabilité d’obtenir un numéro qui soit un nombre premier est alors 0,375.
Exercice 4. 10 points
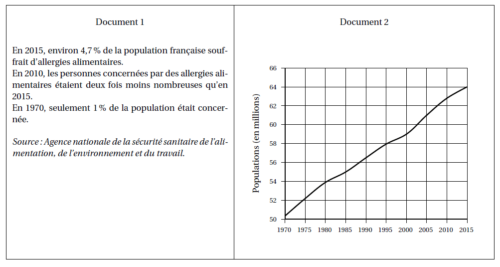
Les données et les questions de cet exercice concernent la Francemétropolitaine.
Partie 1 :
1. Déterminer une estimation du nombre de personnes, à 100 000 près, qui souffraient d’allergies alimentaires en France
en 2010.
2. Est-il vrai qu’en 2015, il y avait environ 6 fois plus de personnes concernées qu’en 1970?
Partie 2 :
En 2015, dans un collège de 681 élèves, 32 élèves souffraient d’allergies alimentaires.
Le tableau suivant indique les types d’aliments auxquels ils réagissaient.
1. La proportion des élèves de ce collège souffrant d’allergies alimentaires est-elle supérieure à celle de la population française?
2. Jawad est étonné : « J’ai additionné tous les nombres indiqués dans le tableau et j’ai obtenu 39 au lieu de 32 ».
Expliquer cette différence.
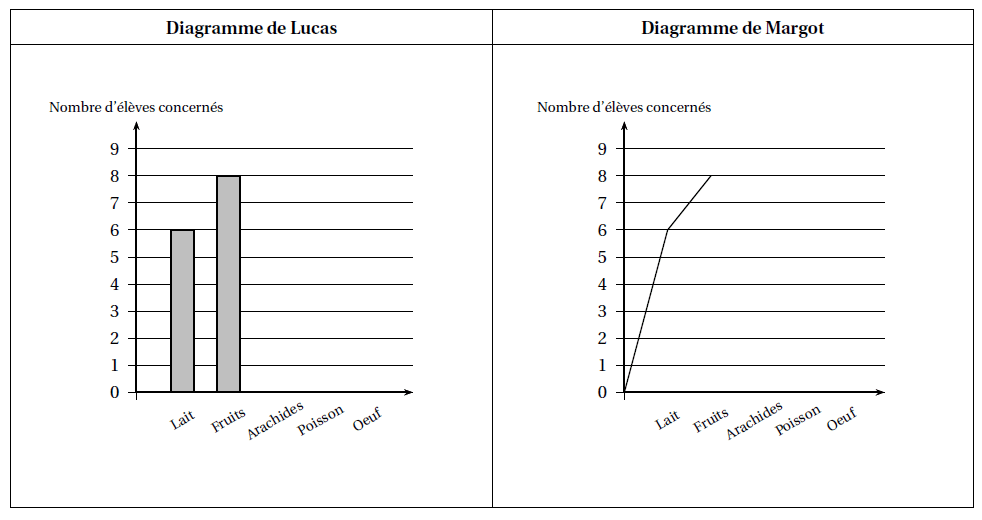
3. Lucas etMargot ont chacun commencé un diagramme pour représenter les allergies des 32 élèves de leur collège :
3. a. Qui de Lucas ou deMargot a fait le choix le mieux adapté à la situation? Justifier la réponse.
3. b. Reproduire et terminer le diagramme choisi à la question a.
Exercice 5. 5 points
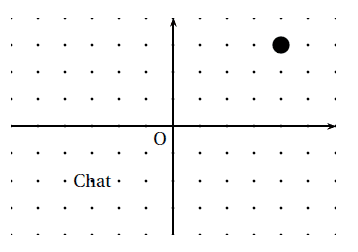
L’image ci-dessous représente la position obtenue au déclenchement du bloc départ d’un programme de jeu.
L’arrière-plan est constitué de points espacés de 40 unités.
Dans cette position, le chat a pour coordonnées (−120 ; −80).
Le but du jeu est de positionner le chat sur la balle.
1. Quelles sont les coordonnées du centre de la balle représentée dans cette position?
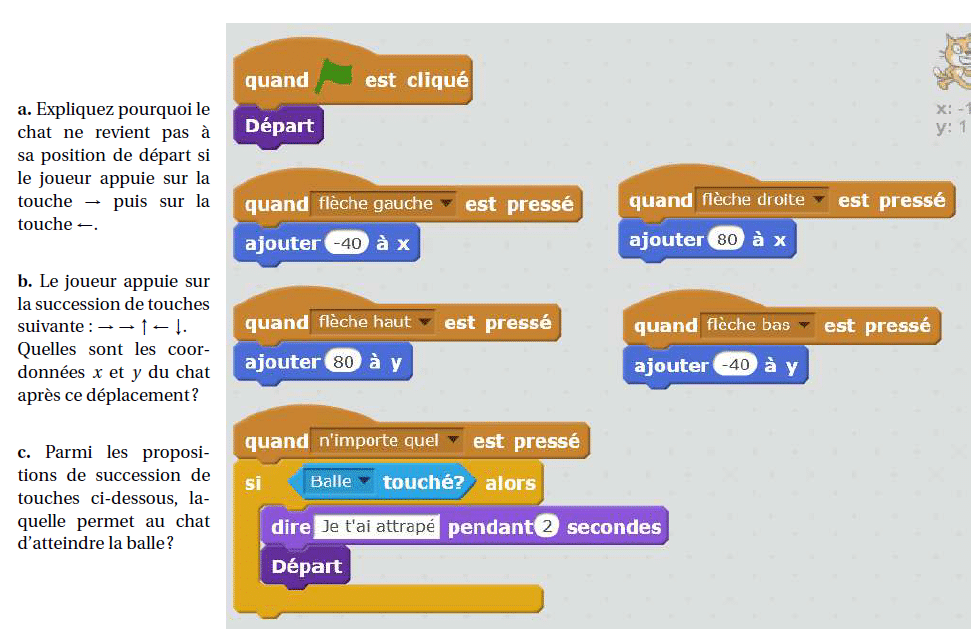
2. Dans cette question, le chat est dans la position obtenue au déclenchement du bloc départ.
Voici le script du lutin « chat » qui se déplace.
3. Que se passe-t-il quand le chat atteint la balle?
Exercice 6. 10 points
Le schéma ci-dessous représente le jardin de Leïla. Il n’est pas à l’échelle.
[OB] et [OF] sont des murs, OB = 6met OF = 4m.
La ligne pointillée BCDEF représente le grillage que Leïla veut installer pour délimiter un enclos rectangulaire OCDE.
Elle dispose d’un rouleau de 50m de grillage qu’elle veut utiliser entièrement.
Leila envisage plusieurs possibilités pour placer le point C.
1. En plaçant C pour que BC = 5 m, elle obtient que FE = 15 m.
1. a. Vérifier qu’elle utilise les 50m de grillage.
1. b. Justifier que l’aire A de l’enclos OCDE est 209 m².
2. Pour avoir une aire maximale, Leïla fait appel à sa voisine professeure de mathématiques qui, un peu pressée, lui écrit sur un bout de papier :
« En notant BC = x, on a A(x)= −x² +18x +144 »
Vérifier que la formule de la voisine est bien cohérente avec le résultat de la question 1.
3. Dans cette partie, les questions a. et b. ne nécessitent pas de justification.
3. a. Leïla a saisi une formule en B2 puis l’a étirée jusqu’à la cellule 12.
Quelle formule est alors inscrite dans la cellule F2?
3. b. Parmi les valeurs figurant dans le tableau, quelle est celle que Leïla va choisir pour BC afin obtenir un enclos d’aire maximale?
3. c. Donner les dimensions de l’enclos ainsi obtenu.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet des Collèges 2017 Amérique du Nord 7 juin 2017» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
