Les fonctions affines : corrigé des exercices de maths en 3ème en PDF.
Mis à jour le 4 septembre 2025
Exercice 1 :
Expliquer ce que signifie les notations suivantes :
a. f : x 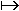
b. f(x)= -2x+3 : la fonction f définie par l’image de tout nombre x est -2x+3
Exercice 2:
Parmi les fonctions données, indiquer celles qui sont affines, celles qui sont linéaires, celles qui ne sont pas affines.
est affine .
est affine.
est linéaire
est affine, c’est une fonction constante .
est ni linéaire ni affine.
est linéaire .
est ni linéaire ni affine.
est ni linéaire ni affine.
Exercice 3 :
La fonction f est définie par : x 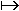
a. Calculer f(2)=-8 ;f(- 3)=17 ; f(0)=2.
b. Calculer l’image de 4 : f(4)= -18
c. Calculer le nombre x tel que :
.
Exercice 4 :
On donne les images de deux nombres par une fonction affine f.
f(3)=5 et f(7)=13
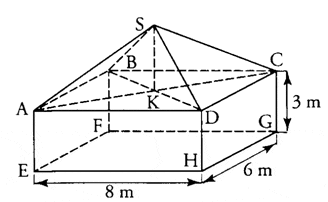
a. Tracer sa représentation graphique dans un repère.
b. Déterminer l’expression algébrique de cette fonction f : x 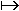
donc
Conclusion :
Exercice 6 :
g(x)=3x
u(x)=2
f(x)=x+2,5
h(x)=-2x-2
k(x)=-3,5x+0,5
Exercice 7 :
Les droites sont parallèles car le coefficient directeur est le même.
Exercice 8 :
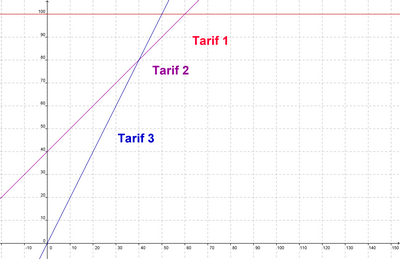
a.Pour le tarif 1, il paiera 100 €.
Pour le tarif 2, il paiera : 40+12×1=52 €
Pour le tarif 3 , il paiera : 12×2= 24 €
Dans ce cas, le tarif 3 est le plus intéressant.
b. On appelle x le nombre de fois où Yéro ira à la piscine.
Exprimer, en fonction de x :
t1(x)=100
t2(x)= x+40
t3(x)= 2x
c. Représenter graphiquement ces trois fonctions dans un même repère orthogonal.
d. Il devra payer 12×4 = 48 entrées.
Et s’il y va deux fois par semaine ?
le double soit 96 entrées .
e. Pour 48 entrées, c’est le tarif 2 et pour 96 c’est le tarif 1.
f. A partir de 61 entrées, le tarif 1 est le plus intéressant.
Exercice 9 :
1)Sois la fonction affine f définie par f(x)=-2x+3 .
a) calculer f(0) .
f(0)= -2×0+3=3
b) calculer l’antécédent de 5 .
fx()=5
-2x+3=5
-2x=5-3
-2x=2
x=-1
Donc l’antécédent de 5 par la fonction f est – 1 .
2) Soit la fonction affine g telle que g(-2)=-2 et g(3)=4 .
a) déterminer la fonction g .
et
Conclusion : la fonction affine g recherchée est
b) calculer g(0) et g(3) .
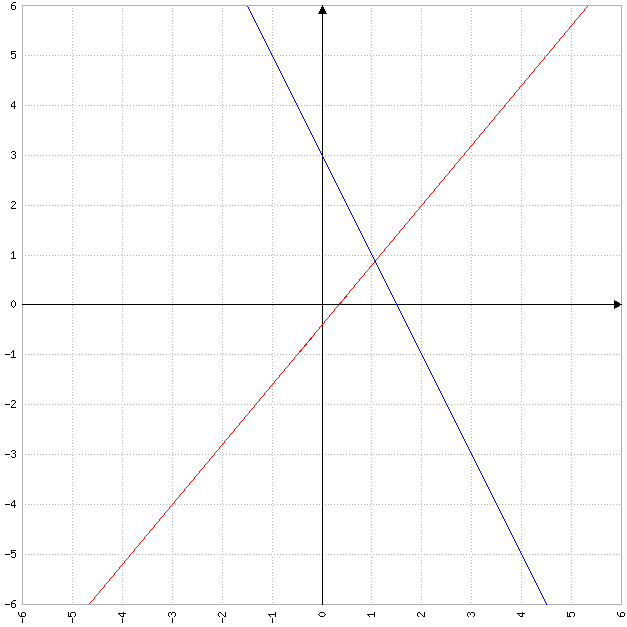
3) dans un même repère (O,I,J).
a) tracer les représentations graphiques de f et de g .
b) calculer les coordonnées du point d’intersection de ces représentations graphiques .
Résolvons f(x) = g(x)
et
Les coordonnées du point d’intersection sont : .
Exercice 10 :
Pour le paiement de la garderie dans une école, on propose deux formules.
– Formule A : on paie 40 € pour devenir adhérent pour l’année scolaire puis on
paye 10 € par mois de garderie.
-Formule B : pour les non adhérents, on page 18 € par mois.
1. On appelle le nombre de mois de garderie.
et
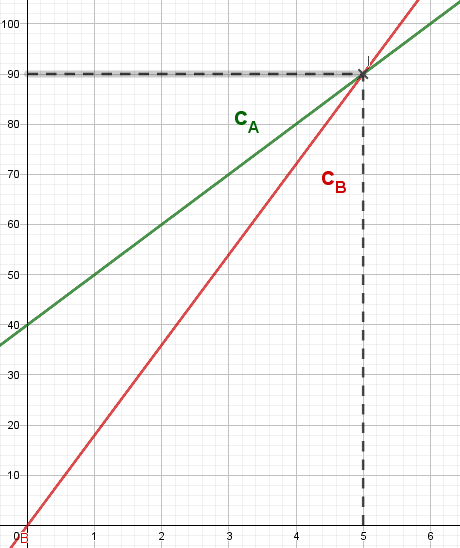
2. Représentez graphiquement les fonctions suivantes dans un repère :
et
.
On prendra 1 cm pour 1 mois en abscisse et 1 cm pour 10 € en ordonnée.
3.
a) C’est le point d’intersection des deux droites. Pour 9 mois, les prix à payer sont égaux.
b) Retrouver ce résultat par le calcul.
4. La plus avantageuse si on ne paie que 4 mois dans l’année est la formule B.
5. On dispose d’un budget de 113 €.
Nous sommes amenés à résoudre cette équations :
On pourra payer, au maximum, 7 mois de garderie avec un budget de 113 euros.
Exercice 11 :
Dans chacun des cas suivants, écrivez la fonction f sous la forme f(x)=ax+b
et précisez les valeurs de a et b.
1) La représentation graphique de f est une droite de coefficient directeur -3 et telle que f(0)=2.
a= – 3 donc f(x)=-3x+b
de plus f(0)= – 2
donc -3×0+b= – 2
b= – 2
donc f(x)= – 3x – 2
2)La fonction f est la fonction qui, à un nombre x, lui ajoute 6 et multiplie le résultat par – 4.
f(x)= – 4(x+6) = -4x-24
3) La fonction f est la fonction qui, à un nombre x, le multiplie par 3, ajoute 4 au résultat,
puis divise le tout par 2.
4) La fonction f est définie par f(x)=(x+1)²-x².
5). La fonction f est telle que si les x augmentent de 3, les « f(x) » augmentent de 12.
De plus, f(0)=1.
et f(x)=4x+b
de plus f(0)=4×0+b=1
donc b=1
d’où f(x) = 4x+1
Exercice 12 :
On désigne par la hauteur SK (exprimée en mètres) de la pyramide SABCD.
1) Montrer que le volume (en m3) de la serre est donné par la formule x .
2) Calculer ce volume pour x = 1,5.
3) Pour quelle valeur de le volume de la serre est-il de 200 m3 ?
La hauteur de la pyramide doit être de 3,25 m afin que le volume soit de 200 .
Exercice 13 :
1. A vous de compléter le tableau.
2. a.
b.
3.
4.
a. Pour 6 cartouches, c’est le prix A qui est le plus avantageux.
b. Pour 80 euros, il est plus intéressant de choisir la formule B.
5.
Cherchons pour quel nombre de cartouches les prix sont égaux :
Les prix sont égaux pour 8 cartouches achetées.
Le prix internet est inférieur au delà de 8 cartouches.
Exercice 14 :
L’école décide de tester un logiciel pour gérer sa bibliothèque. Elle télécharge ce logiciel sur
Internet.
1. Le fichier a une taille de 3,5 Mo (Mega-octets) et le téléchargement s’effectue en 7 secondes.
Quel est le débit de la connexion Internet ? On donnera le résultat en Mo/s.
c’est une situation de proportionnalité.
donc
Après une période d’essai de 1 mois, l’école décide d’acheter le logiciel.
Il y a trois tarifs :
• Tarif A : 19 €
• Tarif B : 10 centimes par élève
• Tarif C : 8 € + 5 centimes par élève
2. Compléter le tableau suivant :
| Nombre d’élèves | 100 | 200 | 300 |
| Tarif A | 19 € | ||
| Tarif B | 30 € | ||
| Tarif C | 18 € |
3. a. Si x représente le nombre d’élèves, laquelle des expressions suivantes correspond au tarif C ?
C1 = 8 + 5x
C2 = 8 + 0, 05x
C3 = 0, 05 + 8x
b. Est ce une situation de proportionnalité ? Justifier la réponse.
C2 correspond à une fonction affine donc ce n’est pas une situation de proportionnalité, il y aurait fallu une fonction linéaire (c’est le cas du tarif B).
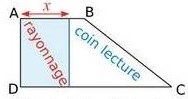
Exercice 17 :
a. L’aire totale est :
.
b. x est compris entre 0 et 5.
c.
d.
e. Nous observons graphiquement que les voeux de la documentaliste
seront pris en compte lorsque x = 5.
et par le calcul :
10x=65-5x
10x+5x=65
15x=65
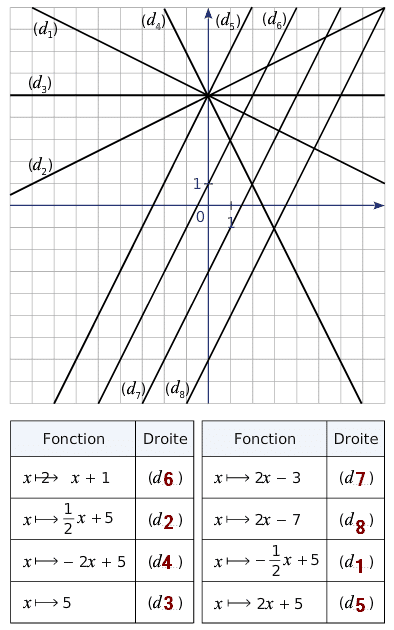
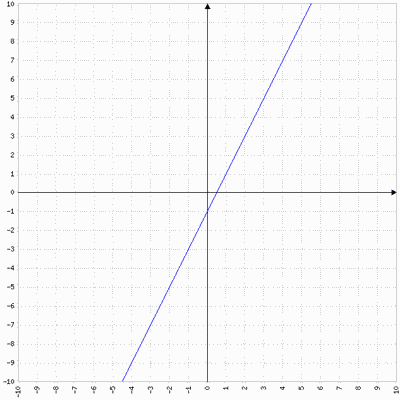
Exercice 18 :
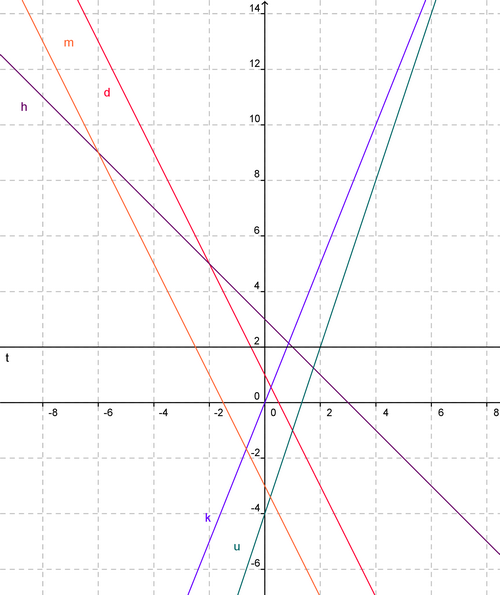
Par lecture graphique, indiquer pour chaque fonction affine, quelle droite est sa représentation graphique.
Exercice 19 :
Déterminer la fonction affine f telle que f(9)=-1 et f(18)= – 8.
Déterminons la valeur du coefficient directeur a :
donc la fonction f est définie par
or f(9)=-1 donc
donc
Conclusion :
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les fonctions affines : corrigé des exercices de maths en 3ème en PDF.» au format PDF.
Ressources de troisième
Cours de troisième
Exercices de troisième
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.



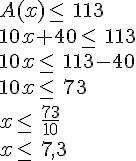
.png)