Brevet de maths 2021 : sujet blanc n° 2 en PDF pour réviser.

brevet de maths

BREVET de MATHS 2021

SUJET BLANC N° 2

_______________
Durée de l’épreuve : 2 h 00
_______________
L’utilisation de la calculatrice est autorisée
(circulaire n°99-186 du 16 novembre 1999)
L’usage du dictionnaire n’est pas autorisé

Exercice 1 :

Un pâtissier a préparé 840 financiers et 1 176 macarons. Il souhaite faire des lots, tous identiques,
en mélangeant financiers et macarons. Il veut utiliser tous les financiers et tous les macarons.
1. Sans faire de calcul, expliquer pourquoi les nombres 840 et 1 176 ne sont pas premiers entre
eux.
2. Le pâtissier peut-il faire 21 lots ? Si oui, calculer le nombre de financiers et le nombre de
macarons dans chaque lot.
3. Quel est le nombre maximum de lots qu’il peut faire ? Quelle sera alors la composition de
chacun des lots ?

Exercice 2 :

Cédric s’entraîne pour l’épreuve de vélo d’un triathlon.
La courbe ci-dessous représente la distance en kilomètres en fonction du temps écoulé en minutes.

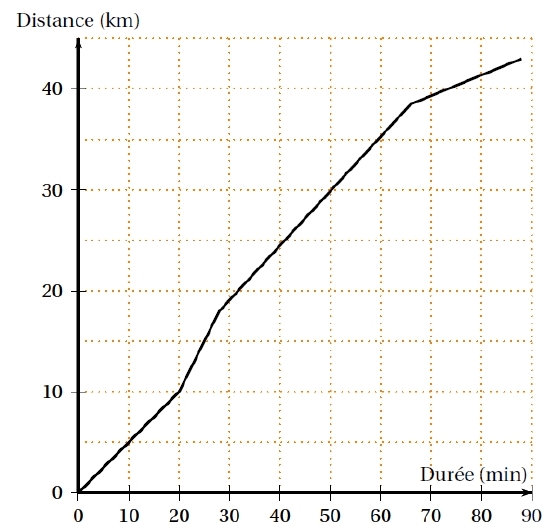
Pour les trois premières questions, les réponses seront données grâce à des lectures graphiques.
Aucune justification n’est attendue sur la copie.
1. Quelle distance Cédric a-t-il parcourue au bout de 20 minutes ?
2. Combien de temps a mis Cédric pour faire les 30 premiers kilomètres ?
3. Le circuit de Cédric comprend une montée, une descente et deux portions plates.
Reconstituer dans l’ordre le trajet parcouru par Cédric.
4. Calculer la vitesse moyenne de Cédric (exprimée en km/h) sur la première des quatre parties
du trajet.

Exercice 3 :

Dans cet exercice, les figures codées ne sont pas en vraie grandeur.
Chacune des affirmations suivantes est-elle vraie ou fausse ?
Toutes les réponses doivent être justifiées.
Affirmation 1 :

Le volume de ce solide est $56\,cm^3$ .

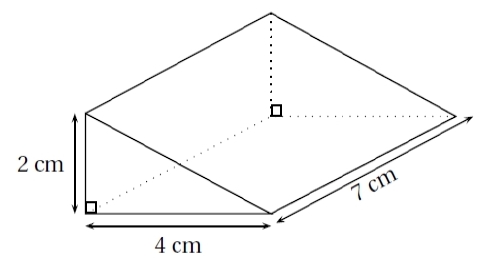
Affirmation 2 :

Les droites (ML) et (NO) sont parallèles.

Affirmation 3 :

La diagonale d’un carré d’aire 36 cm² a pour longueur $6\sqrt{2}$ cm.
Affirmation 4 :

0 a un seul antécédent par la fonction qui à tout nombre x associe 3x +5.

Exercice 4 :

On s’intéresse à la zone au sol qui est éclairée la nuit par deux sources de lumière : le lampadaire
de la rue et le spot fixé en F sur la façade de l’immeuble.

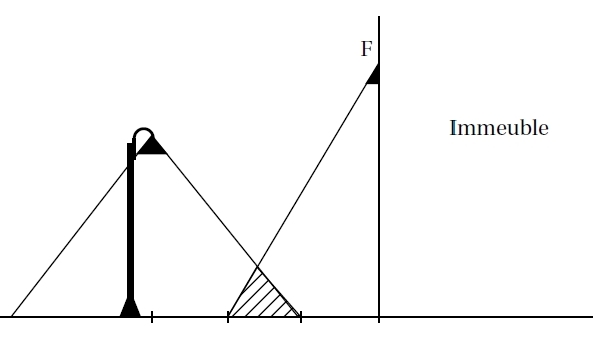
On dispose des données suivantes :
PC = 5,5 m ; CF = 5 m ; HP = 4 m ;
$\widehat{MFC},=,33,^{\circ}$ ; $\widehat{PHL},=,40,^{\circ}$

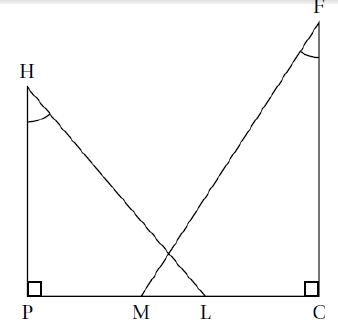
1. Justifier que l’arrondi au décimètre de la longueur PL est égal à 3,4 m.
2. Calculer la longueur LM correspondant à la zone éclairée par les deux sources de lumière.
On arrondira la réponse au décimètre.
3. On effectue des réglages du spot situé en F afin que M et L soient confondus.
Déterminer la mesure de l’angle $\widehat{MFC}$ . On arrondira la réponse au degré.

Exercice 5 :

Dans cet exercice, on considère le rectangle ABCD ci-contre tel que son périmètre soit égal à 31 cm.

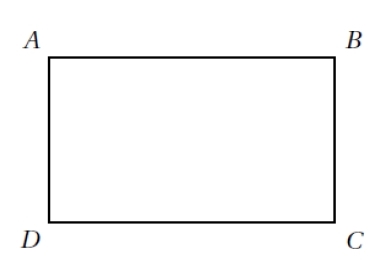
1. a. Si un tel rectangle a pour longueur 10 cm, quelle est sa largeur ?
b. On appelle x la longueur AB. En utilisant le fait que le périmètre de ABCD est de 31 cm,
exprimer la longueur BC en fonction de x.
c. En déduire l’aire du rectangle ABCD en fonction de x.
2. On considère la fonction f définie par f (x) = x(15,5−x).
a. Calculer f (4).
b. Vérifiez qu’un antécédent de 52,5 est 5.

3. Sur le graphique ci-dessous, on a représenté l’aire du rectangle ABCD en fonction de la
valeur de x.

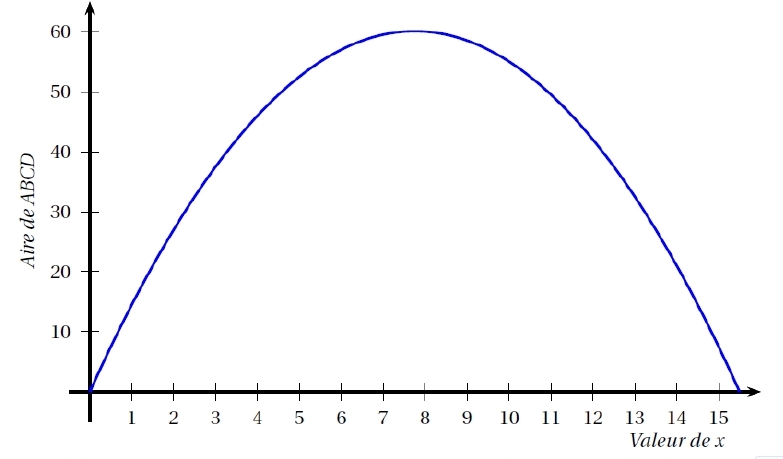
À l’aide de ce graphique, répondre aux questions suivantes en donnant des valeurs approchées :
a. Quelle est l’aire du rectangle ABCD lorsque x vaut 3 cm ?
b. Pour quelles valeurs de x obtient-on une aire égale à 40 cm² ?
c. Quelle est l’aire maximale de ce rectangle ? Pour quelle valeur de x est-elle obtenue ?
4. Que peut-on dire du rectangle ABCD lorsque AB vaut 7,75 cm ?

Exercice 6 :

En se retournant lors d’une marche arrière, le conducteur d’une camionnette voit le sol à 6 mètres
derrière son camion.

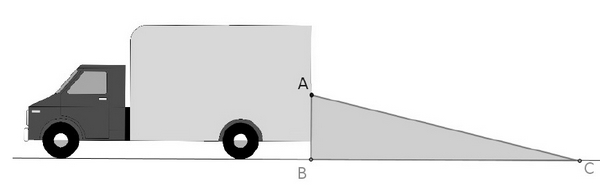
Sur le schéma, le triangle grisé correspond à ce que le conducteur ne voit pas lorsqu’il regarde en
arrière.
Données : AB = 1,50 m et BC = 6 m
Une fillette mesure 1,10 m. Elle passe à 1,40 m derrière la camionnette.
Le conducteur peut-il la voir ? Expliquer.

Consulter le corrigé en ligne

Cette publication est également disponible en : English (Anglais) Español (Espagnol) العربية (Arabe)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet de maths 2021 : sujet blanc n° 2 en PDF» au format PDF.

D'autres fiches dans la section brevet de maths

Télécharger nos applications gratuites avec tous les cours et exercices corrigés.

D'autres fiches similaires à brevet de maths 2021 : sujet blanc n° 2 en PDF.

Annales du brevet de maths 2023 : réviser le DNB de maths.
72
Des extraits de sujets du brevet de maths 2023 classés par chapitres. Ces extraits vous permettent de réviser le brevet des collèges afin de vous préparer dans les meilleurs conditions. En complément de tous les sujets du brevet de maths des sessions antérieures, Mathovore met à votre disposition des extraits…
Théorème de Pythagore : exercices de maths en 4ème corrigés en PDF
65
Des exercices de maths en quatrième (4ème) sur le théorème de Pythagore simples et plus compliqués ainsi que des problèmes à résoudre corrigés. Exercice 1 - Carte géographique. Sur une carte, le triangle CLP formé par les villes de Caen, Lisieux et Pont-l‘Evêque est considéré comme étant rectangle en L.…
Brevet Maths 2022 : sujet blanc pour réviser le brevet
63
BREVET BLANC DE MATHÉMATIQUES Session : MAI 2022 Durée de l’épreuve : 2 heures Notation sur 50 points. Exercice 1 : ( 12 points) 1. Dans cet exercice, on considère le rectangle ABCD ci-contre tel que son périmètre soit égal à 32 cm. On appelle la longueur AB. a. Représenter…

Les dernières fiches mises à jour.

Voici les dernières ressources similaires à brevet de maths 2021 : sujet blanc n° 2 en PDF mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.

Mathovore c'est 13 625 065 cours et exercices de maths téléchargés en PDF.