AMÉRIQUE DU SUD
Brevet de mathématiques
Le 1er décembre 2016
Durée : 2h00
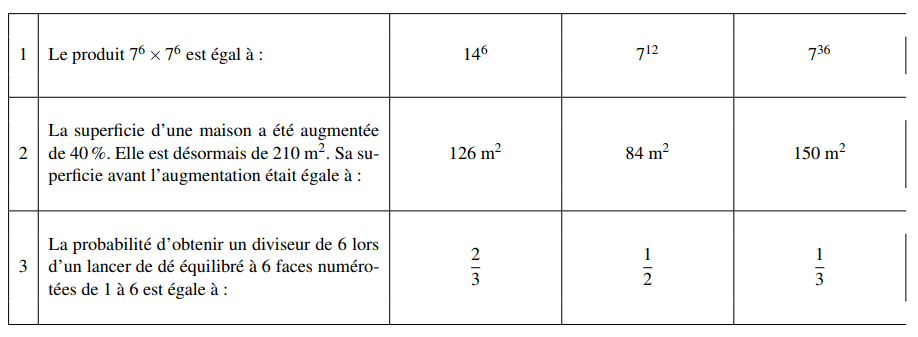
EXERCICE 1 : 6 points
Cet exercice est un questionnaire à choix multiples (QCM).
Pour chaque ligne du tableau, trois réponses sont proposées, mais une seule est exacte.
Toute réponse exacte vaut 2 points.
Toute réponse inexacte ou toute absence de réponse n’enlève pas de point.
Indiquer sur la copie le numéro de la question et, sans justifier, recopier la réponse exacte.
EXERCICE 2 : 6 points
Un avion de ligne transportant des passagers atterrit à l’aéroport international Galeao à Rio de Janeiro.
On étudie la distance de freinage de l’appareil en fonction de sa vitesse au moment de l’atterrissage.
Le pilote peut décider d’un freinage « rapide » s’il souhaite raccourcir la distance de freinage, ou d’un freinage « confort »
plus modéré et donc plus confortable pour les passagers.
Les courbes suivantes donnent la distance de freinage d’un avion en fonction de sa vitesse au moment de l’atterrissage selon
le mode freinage choisi (confort ou rapide).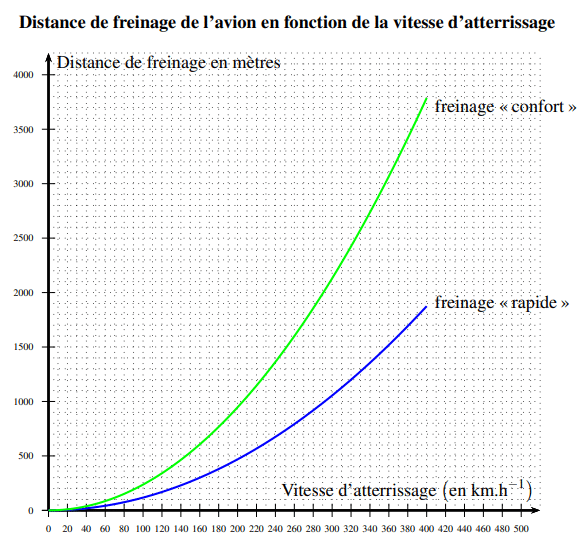
1. Donner par lecture graphique, sans justification :
(a) Une valeur approchée de la distance de freinage « confort » de l’appareil si l’avion arrive à une vitesse de
.
(b) Une valeur approchée de la vitesse d’atterrissage d’un avion dont la distance de freinage « rapide » est de 1 500 m.
2. Pour regagner la zone de débarquement des passagers, l’avion doit emprunter une des quatre sorties précisées dans
les documents ci-dessous :
(a) L’avion atterrit à . Le pilote décide un freinage « confort ».
Avec la distance de freinage correspondante, quelle est ou quelles sont les sorties qu’il va dépasser ?
(b) Seule la sortie 1 étant disponible, le pilote envisage un freinage « rapide ». Déterminer avec la précision du
graphique, la vitesse maximale avec laquelle il peut atterrir pour pouvoir emprunter cette sortie.
EXERCICE 3 : 5 points
Carole souhaite réaliser une mosaïque sur un mur de sa maison. La surface à paver est un rectangle de dimensions 108 cm
et 225 cm et doit être entièrement recouverte par des carreaux de faïence carrés de même dimension sans découpe.
1. Carole peut-elle utiliser des carreaux de 3 cm de côté ? De 6 cm de côté ?
2. Quelle est la dimension maximale des carreaux que Carole peut poser ? Combien de carreaux utilisera-t-elle ?
EXERCICE 4 : 3 points
Cristo Redentor, symbole brésilien, est une grande statue dominant la ville de Rio qui s’érige au sommet du mont Corcovado.
Au pied du monument, Julien et Magali souhaitent mesurer la hauteur de la statue (socle compris). Julien qui mesure 1,90 m,
se place debout à quelques mètres devant la statue. Magali place le regard au niveau du sol de telle manière qu’elle voit le
sommet du Cristo (S) et celui de la tête de Julien (T) alignés; elle se situe alors à 10 m de la statue et à 50 cm de Julien. La
situation est modélisée ci-dessous par la figure qui n’est pas à l’échelle.
Déterminer la hauteur SC de la statue en supposant que le monument et Julien sont perpendiculaires au sol.
EXERCICE 5 : 6 points
Pour monter au sommet du Corcovado et accéder à la statue depuis le centre de Rio, on peut emprunter un minibus. Le prix
d’un billet en Réal brésilien (R$), monnaie brésilienne, comprend le transport vers le site ainsi que l’accès au monument.
On donne les documents suivants.
1. Déterminer le prix de la visite pour un adulte le 09/02/2016.
2. Déterminer le prix de la visite pour un enfant ayant entre 6 ans et 11 ans, le 09/02/2016.
EXERCICE 6 : 4 points
Inauguré en 1950, le stade Maracanà est un lieu mythique, place de grands événements sportifs tels que la coupe du monde
2014 ou les jeux olympiques 2016. C’est une structure de forme ovale de dimensions 317 m et 279 m pour une hauteur
de 32 m dont la surface au sol est d’environ 69 500 m².
Sur la célèbre plage de Copacabana, à Rio, on peut admirer de nombreuses sculptures de sable. L’un des sculpteurs souhaite réaliser une reproduction du stade à l’échelle 1/300.
1. Quelles seront les dimensions arrondies au centimètre de cette reproduction.
2. (a) Quelle en sera la superficie ? On donnera le résultat en m², arrondi au centième.
(b) Le sculpteur dispose d’un espace de 1 m².
Est-il certain de pouvoir réaliser sa reproduction ? On justifiera brièvement la réponse.
EXERCICE 7 : 7 points
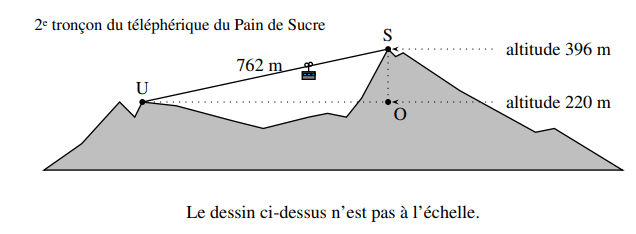
Le mont du Pain de Sucre est un pic situé à Rio à flanc de mer. Il culmine à 396 mètres d’altitude et est accessible par un
téléphérique composé de deux tronçons.
On a représenté ci-dessus le deuxième tronçon du téléphérique qui mène du point U au sommet S du pic.
On donne : Altitude du point S : 396 m US = 762 m
Altitude du point U : 220 m Le triangle UOS est rectangle en O.
1. Déterminer l’angle DUS que forme le câble du téléphérique avec l’horizontale. On arrondira le résultat au degré.
2. Sachant que le temps de trajet entre les stations U et S est de 6 min 30 s, calculer la vitesse moyenne du téléphérique entre
ces deux stations en mètres par seconde. On arrondira le résultat au mètre par seconde.
3. On a relevé la fréquentation du Pain de Sucre sur une journée et saisit ces informations dans une feuille de calcul d’un
tableur.
On a saisi dans la cellule H2 la formule : =SOMME(B2:G2)
3.a Interpréter le nombre calculé avec cette formule.
3.b Quel est le nombre de visiteurs entre 12 h 00 et 14 h 00 ?
3.c Une formule doit être saisie pour calculer le nombre moyen de visiteurs par heure sur cette journée. Parmi les propositions
suivantes, recopier sans justification celle qui convient :
MOYENNE(B2:G2) =MOYENNE(B2:G2)
MOYENNE(B2:G2)/2 =MOYENNE(B2:G2)/2
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet Amérique 2016 : sujet du brevet de mathématiques» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
