Voici le sujet du brevet de maths 2025 donné en Amérique du Nord, suivi de son corrigé détaillé : une épreuve de deux heures notée sur 100 points, idéale pour s’entraîner au DNB en fin de troisième.
Le premier exercice réunit cinq situations indépendantes : une probabilité dans une urne, la décomposition en facteurs premiers de 1050, une hausse en pourcentage, l’aire d’un polygone agrandi et la moyenne puis la médiane d’une série de tailles. Puis le deuxième mobilise le théorème de Pythagore, sa réciproque sous forme de droites parallèles, le théorème de Thalès et la trigonométrie dans un triangle rectangle. Viennent ensuite deux programmes de calcul traités par le calcul littéral, la lecture d’une courbe distance-temps avec des vitesses moyennes, et enfin des scripts Scratch qui tracent triangle, hexagone et losange.
Pour en tirer le meilleur profit, compose d’abord en temps limité, sans calculatrice au début, puis confronte chacune de tes réponses à la correction rédigée sous le sujet : elle détaille la démarche, les justifications attendues par le correcteur et les résultats encadrés.
L’essentiel : Corrigé du brevet de maths Amérique du nord 2025, avec : chaque question est résolue avec les calculs et la méthode attendue. Idéal pour réviser l’examen en se corrigeant ; corrigé gratuit en PDF.
DIPLÔME NATIONAL DU BREVET
SESSION 2025
MATHÉMATIQUES
AMERIQUE DU NORD
Série générale
Durée de l’épreuve : 2 h 00 – 100 points
Exercice 1 (20 points) (brevet 2025 Nord)
Dans cet exercice, les cinq situations sont indépendantes. Il est rappelé que chaque réponse
doit être justifiée sauf indication contraire.
• Situation 1
Dans une urne de 40 boules indiscernables au toucher, 5 sont rouges, 20 sont vertes et 15 sont
blanches. L’expérience consiste à tirer au hasard une boule de l’urne et à noter sa couleur.
Calculer la probabilité d’obtenir une boule verte.
• Situation 2
Décomposer en produit de facteurs premiers le nombre 1050. Aucune justification n’est
attendue.
• Situation 3
Un article coûte 25 €. Calculer son prix après une augmentation de 14 %.
• Situation 4
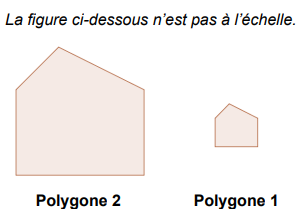
Le polygone 2 est un agrandissement du
polygone 1.
Le coefficient de cet agrandissement est 2,5.
L’aire du polygone 1 est égale à 7,5 cm².
Calculer l’aire du polygone 2.
• Situation 5
Dans une classe de 3e on note la répartition des tailles des élèves dans le tableau suivant :
| Taille (en cm) | 152 | 157 | 160 | 162 | 165 | 170 | 174 | 180 |
| Effectif | 2 | 4 | 2 | 5 | 2 | 4 | 6 | 5 |
a) Quelle est la moyenne des tailles des élèves de cette classe ?
b) Quelle est la médiane des tailles des élèves de cette classe ?
Exercice 2 (20 points)
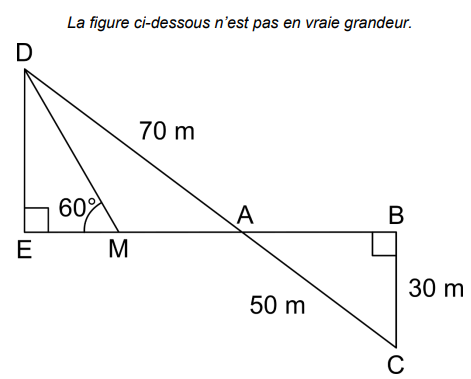
La figure ci-dessous n’est pas en vraie grandeur.
On a les données suivantes :
– Les points A, B, E et M sont alignés
– Les points A, C et D sont alignés
– ADE est un triangle rectangle en E
– ABC est un triangle rectangle en B
– AD = 70 m
– BC = 30 m
– AC = 50 m
– \(\widehat{DME} = 60^\circ\)
1) Calculer la longueur AB.
2) Montrer que les droites (DE) et (BC) sont parallèles.
3) Montrer que la longueur DE est égale à 42 m.
4) Montrer que la longueur EM est environ égale à 24,2 m.
5) En déduire l’aire du triangle AMD.
Exercice 3 (20 points) (brevet 2025 Nord)
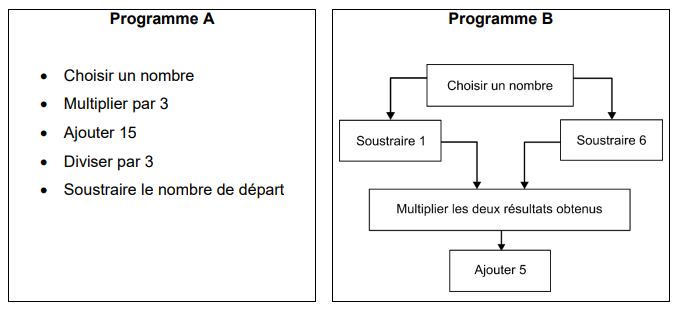
On considère les deux programmes de calcul suivants :
Programme A
- Choisir un nombre
- Multiplier par 3
- Ajouter 15
- Diviser par 3
- Soustraire le nombre de départ
Programme B
- Choisir un nombre
- D’une part, soustraire 1 au nombre choisi ; d’autre part, soustraire 6 au nombre choisi
- Multiplier les deux résultats obtenus
- Ajouter 5
1) Montrer que, lorsque le nombre choisi est 4, le résultat obtenu avec le programme A
est 5.
2) Montrer que, lorsque le nombre choisi est – 2, le résultat obtenu avec le programme A
est 5.
3) Justifier que l’affirmation suivante est vraie :
« Le programme A donne toujours le même résultat. »
4) Lorsque le nombre choisi est 10, quel résultat obtient-on avec le programme B ?
5) Il existe exactement deux nombres pour lesquels les programmes A et B fournissent à
chaque fois des résultats identiques.
Quels sont ces deux nombres ?
Exercice 4 (20 points)
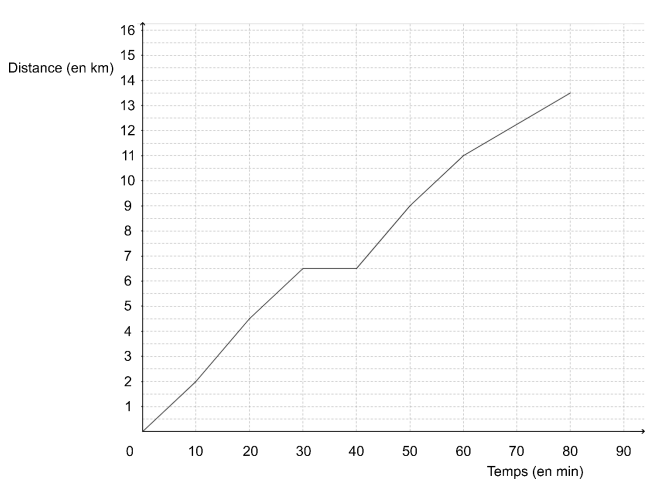
À l’approche d’une course organisée par son collège, Malo s’entraîne sur un parcours de
13,5 km.
La courbe ci-dessous représente la distance parcourue par Malo (en kilomètres) en fonction
du temps écoulé (en minutes).
1) Le temps et la distance parcourue par Malo sont-ils proportionnels ?
2) Quelle distance Malo a-t-il parcourue au bout de 20 minutes ?
Aucune justification n’est attendue.
3) Combien de temps a-t-il mis pour faire les 9 premiers kilomètres ?
Aucune justification n’est attendue.
4) Quelle est la vitesse moyenne de Malo lors de cette course ? Exprimer le résultat au
dixième de km/h près.
5) Louise et Hillal ont couru sur le même parcours de 13,5 km. Louise à une vitesse
régulière égale à 12 km/h et Hillal a une vitesse régulière égale à 10 km/h.
a. Sachant que Louise et Hillal sont partis en même temps, qui a été le premier à
franchir la ligne d’arrivée ?
b. Quelle distance sépare Louise et Hillal, lorsque le premier des deux franchit la ligne
d’arrivée ?
Exercice 5 (20 points) (brevet 2025 Nord)
Dans cet exercice, aucune justification n’est attendue.
Partie 1 : les motifs
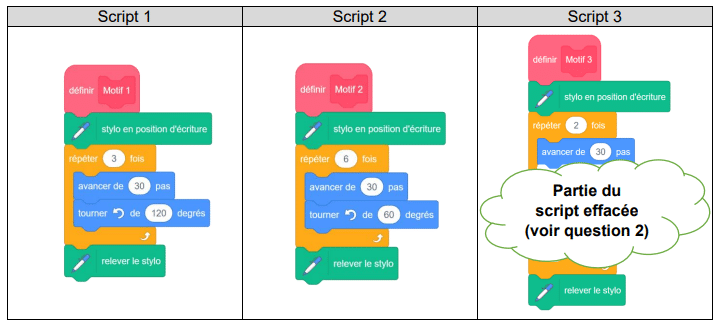
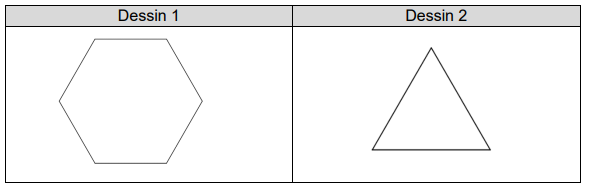
1) Les scripts 1 et 2 permettent chacun d’obtenir un des dessins ci-dessous. Associer chacun
des scripts à son dessin.
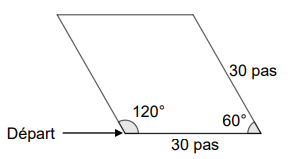
2) Le script 3 permet d’obtenir le losange ci-dessous.
La partie du script effacée contient les 3 instructions
A, B et C ci-dessous.
Sur votre copie, recopier dans le bon ordre les
instructions cachées.
Chaque instruction ne doit être utilisée qu’une seule fois.
| Instruction A | Instruction B | Instruction C |
| tourner ↺ de 60 degrés | tourner ↺ de 120 degrés | avancer de 30 pas |
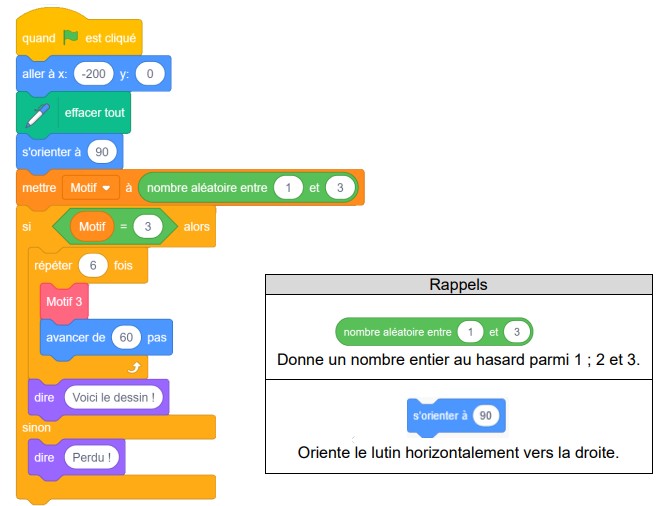
Partie 2 : le script principal
3) Quelles sont les coordonnées du point de départ du lutin ?
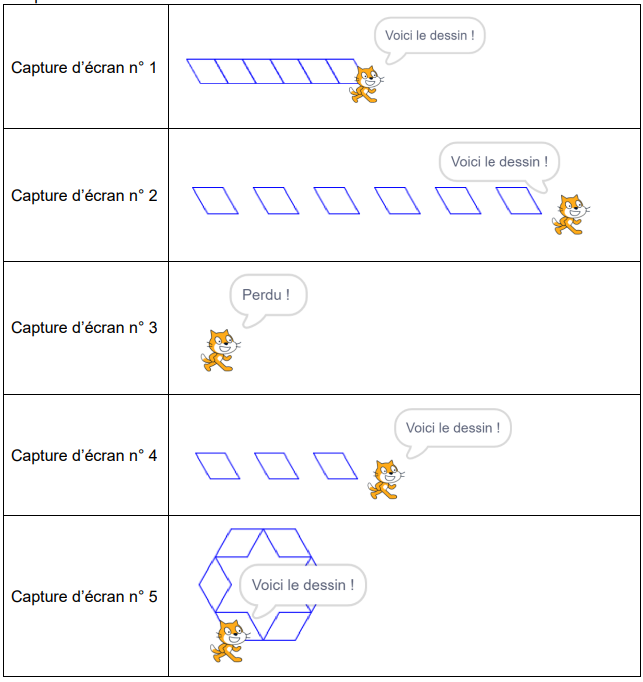
4) Parmi les 5 captures d’écran proposées ci-dessous, seules deux sont possibles.
Lesquelles ?
5) On clique sur le drapeau vert, et on observe le message affiché.
Quelle est la probabilité que le message affiché soit « Voici le dessin ! » ?
6) On lance de nouveau le programme 100 fois et on regroupe les résultats obtenus dans le
tableau suivant :
| Message du lutin | « Voici le dessin ! » | « Perdu ! » |
| Effectif | 40 | 60 |
a) Calculer la fréquence de l’affichage « Voici le dessin ! ».
b) Pourquoi ce résultat est-il différent de celui obtenu à la question 5 ?
Voir le corrigé détaillé : Corrigé du brevet de maths 2025 en Amérique du Nord
Brevet 2025 Nord : méthode de travail
D’abord, cherche chaque exercice seul, sur une feuille de brouillon. Ensuite, compare ta démarche avec la correction, étape par étape. Ainsi, chaque erreur devient une occasion de progresser. Par ailleurs, en outre, quelques minutes par jour suffisent pour retenir l’essentiel.
Par exemple, explique la méthode à voix haute, comme à un camarade. Enfin, le programme officiel de mathématiques est détaillé sur le site Éduscol. Également, tu peux continuer avec brevet de maths 2027 : sujet de référence n° 1 avec énoncé et corrigé.
