Brevet des collèges
La Réunion Antilles–Guyane
Session de rattrapage – 16 septembre 2019
Exercice 1 : 18 points
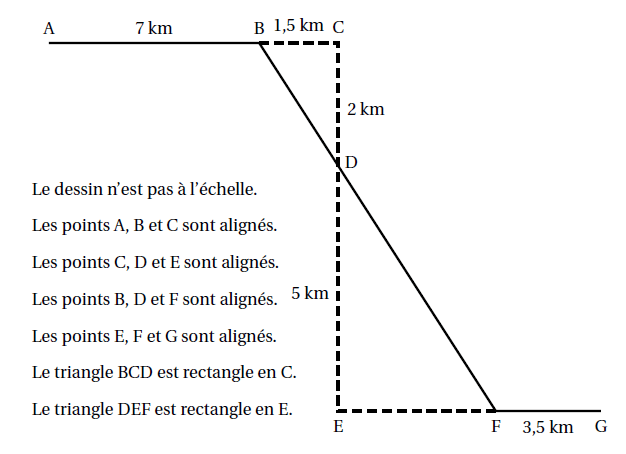
Michel participe à un rallye VIT sur un parcours balisé. Le trajet est représenté en traits pleins.
Le départ du rallye est en A et l’arrivée est en G.
1. Montrer que la longueur BD est égale à 2,5 km.
2. Justifier que les droites (BC) et (EF) sont parallèles.
3. Calculer la longueur DF.
4. Calculer la longueur totale du parcours.
5. Michel roule à une vitesse moyenne de 16 km/h pour aller du point A au point B.
Combien de temps mettra-t-il pour aller du point A au point B?
Donner votre réponse en minutes et secondes.
Exercice 2 : 14 points
1. a. Déterminer la décomposition en produit de facteurs premiers de 2 744.
b. En déduire la décomposition en produit de facteurs premiers de 
.
c. À l’aide de cette décomposition, trouver tel que .
2. Soient a et b deux nombres entiers supérieurs à 2 tels que .
a. Calculer b lorsque a = 100.
b. Déterminer deux nombres entiers a et b supérieurs à 2 et inférieurs à 10 qui vérifient
l’égalité .
Exercice 3 : 17 points
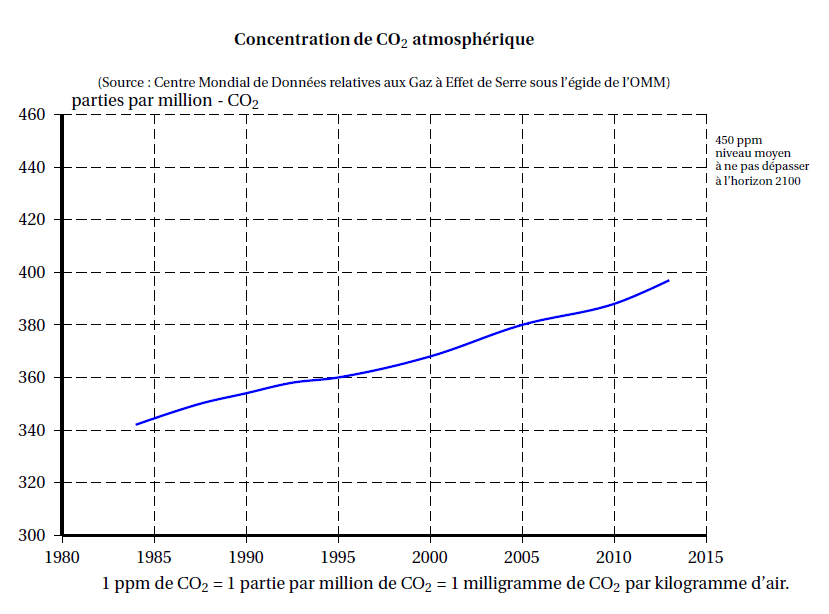
Les activités humaines produisent du dioxyde de carbone (CO2) qui contribue au réchauffement climatique.
Le graphique suivant représente l’évolution de la concentration atmosphérique moyenne
en CO2 (en ppm) en fonction du temps (en année).
1. Déterminer graphiquement la concentration de en ppm en 1995 puis en 2005.
2. On veut modéliser l’évolution de la concentration de en fonction du temps à l’aide d’une
fonction g où g (x) est la concentration de en ppm en fonction de l’année .
a. Expliquer pourquoi une fonction affine semble appropriée pour modéliser la concentration
en en fonction du temps entre 1995 et 2005.
b. Arnold et Billy proposent chacun une expression pour la fonction g :
Arnold propose l’expression ;
Billy propose l’expression .
Quelle expression modélise le mieux l’évolution de la concentration de ? Justifier.
c. En utilisant la fonction que vous avez choisie à la question précédente, indiquer l’année
pour laquelle la valeur de 450 ppm est atteinte.
3. En France, les forêts, grâce à la photosynthèse, captent environ 70 mégatonnes de par an,
ce qui représente 15% des émissions nationales de carbone (année 2016).
Calculer une valeur approchée à une mégatonne près de la masse M du émis en France en
2016.
Exercice 4 : 16 points
Pour le mariage de Dominique et Camille, le pâtissier propose deux pièces montées constituées de
gâteaux de tailles et de formes différentes.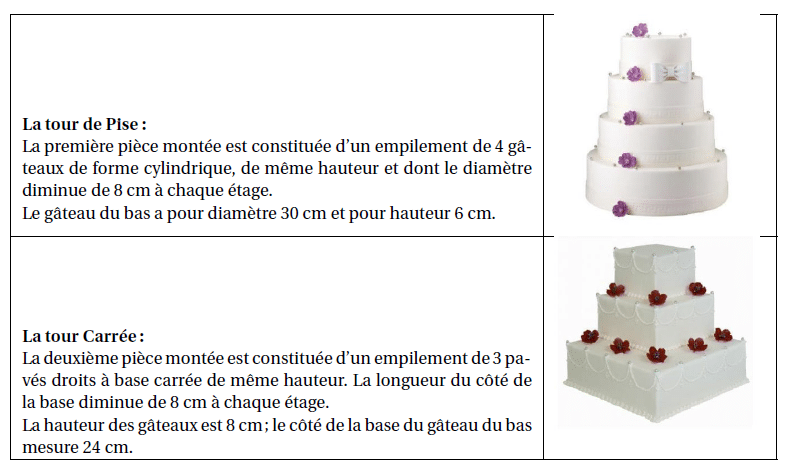
Tous les gâteaux ont été confectionnés à partir de la recette ci-dessous qui donne la quantité des
ingrédients correspondant à 100 g de chocolat.
1. Quel est le ratio (masse de beurre : masse de chocolat) ? Donner le résultat sous forme de fraction
irréductible.
2. Calculer la quantité de farine nécessaire pour 250 g de chocolat noir suivant la recette ci-dessus.
3. Calculer la longueur du côté de la base du plus petit gâteau de la tour Carrée.
4. Quelle est la tour qui a le plus grand volume? Justifier votre réponse en détaillant les calculs.
On rappelle que le volume V d’un cylindre de rayon r et de hauteur h est donné par la formule :
.
Exercice 5 : 15 points
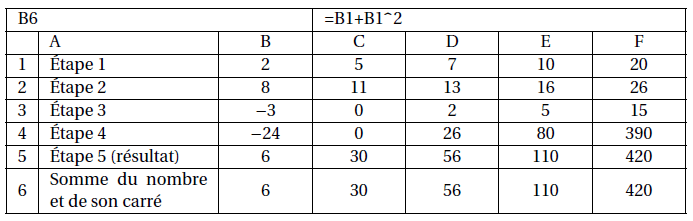
On donne le programme de calcul suivant :
1. a. Montrer que si le nombre choisi est 4, le résultat est 20.
b. Quel est le résultat quand on applique ce programme de calcul au nombre −3?
2. Zoé pense qu’un nombre de départ étant choisi, le résultat est égal à la somme de ce nombre
et de son carré.
a. Vérifier qu’elle a raison quand le nombre choisi au départ vaut 4, et aussi quand on choisit
−3.
b. Ismaël décide d’utiliser un tableur pour vérifier l’affirmation de Zoé sur quelques exemples.
Il a écrit des formules en B2 et B3 pour exécuter automatiquement les étapes 2 et 3 du
programme de calcul.
Quelle formule à recopier vers la droite a-t-il écrite dans la cellule B4 pour exécuter l’étape
4?
c. Zoé observe les résultats, puis confirme que pour tout nombre choisi, le résultat du
programme de calcul est bien . Démontrer sa réponse.
d. Déterminer tous les nombres pour lesquels le résultat du programme est 0.
Exercice 6 : 20 points
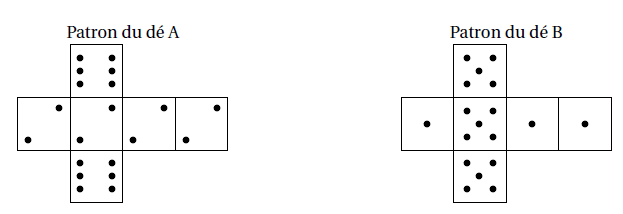
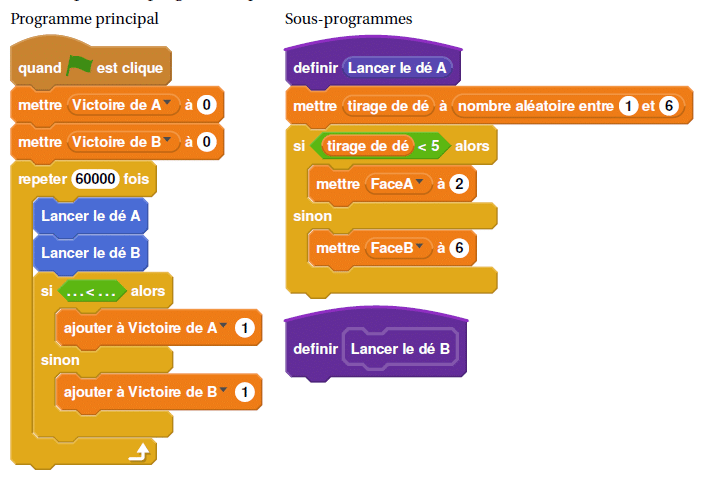
Deux amis Armelle et Basile jouent aux dés en utilisant des dés bien équilibrés mais dont les faces ont
été modifiées. Armelle joue avec le dé A et Basile joue avec le dé B.
Lors d’une partie, chaque joueur lance son dé et celui qui obtient le plus grand numéro gagne un
point.
Voici les patrons des deux dés :
1. Une partie peut-elle aboutir à un match nul ?
2. a. Si le résultat obtenu avec le dé A est 2, quelle est la probabilité que Basile gagne un point ?
b. Si le résultat obtenu avec le dé B est 1, quelle est la probabilité qu’Armelle gagne un point ?
3. Les joueurs souhaitent comparer leur chance de gagner. Ils décident de simuler un match de
soixante mille duels à l’aide d’un programme informatique.
Voici une partie du programme qu’ils ont réalisé.
On précise que l’expression (nombre aléatoire entre 1 et 6) renvoie de manière équiprobable un
nombre pouvant être 1; 2; 3; 4; 5 ou 6.
Les variables Face A et Face B enregistrent les résultats des dés A et B. Par exemple, la variable Face A
peut prendre soit la valeur 2 soit la valeur 6, puisque ce sont les seuls nombres présents sur le dé A.
Les variables Victoire de A et Victoire de B comptent les victoires des joueurs.
1. Lorsqu’on exécute le sous-programme « Lancer le dé A », quelle est la probabilité que la variable
Face A prenne la valeur 2?
2. Recopier la ligne 7 du programme principal en la complétant.
3. Rédiger un sous-programme « Lancer le dé B » qui simule le lancer du dé B et enregistre le
nombre obtenu dans la variable Face B.
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «france rattrapage : sujet du brevet de maths 2019» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
D'autres utilitaires pour progresser en autonomie :
