Brevet de maths 2025 blanc n°2 avec sujet et corrigé.

BREVET BLANC DE MATHS n°2
SESSION 2025
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 – 100 points

Matériel autorisé :
L’usage de la calculatrice avec le mode examen activé est autorisé.
L’usage de la calculatrice sans mémoire, « type collège », est autorisé.
L’utilisation du dictionnaire est interdite.
Le sujet est constitué de cinq exercices indépendants.
Le candidat peut les traiter dans l’ordre qui lui convient.

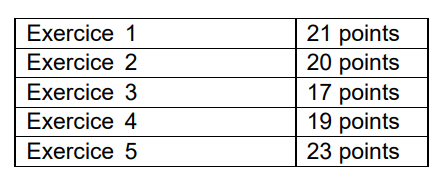
Exercice 1 (21 points)
Dans cet exercice, toutes les questions sont indépendantes.
1. On a décomposé ci-dessous cinq nombres en produits de facteurs premiers.
Parmi ces nombres, lesquels sont divisibles par 21 ?

2. Donner, sans justification, l’écriture scientifique du nombre .
3. La comète Hale-Bopp a atteint la vitesse de 2 640 km/min. Quelle est sa vitesse en m/s ?
4. Quelles sont les solutions de l’équation ?
5. On considère la fonction définie par .
Quelle est l’image de −3 par la fonction ?
6. Sur la figure ci-dessous (qui n’est pas à l’échelle) :

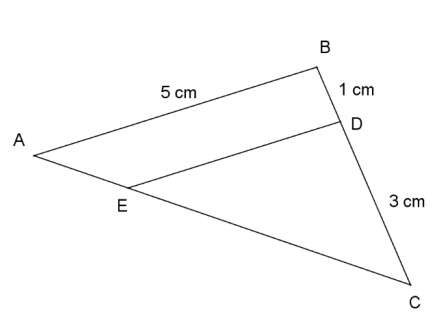
• les points A, E et C sont alignés ;
• les points B, D et C sont alignés ;
• les droites (AB) et (ED) sont parallèles ;
• AB = 5 cm, BD = 1 cm, CD = 3 cm.
Calculer DE.

Exercice 2 (20 points)
On a relevé dans une feuille de calcul les températures maximales Tmax (en °C) atteintes à Strasbourg
le 25 juin de chaque année de 2010 à 2018 (source : meteociel.fr).

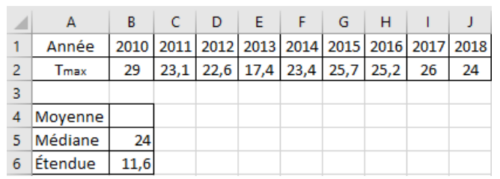
1. On a oublié de calculer la moyenne de cette série.
Quelle formule peut-on saisir dans la cellule B4 pour que ce calcul soit effectué ?
2. Donner, sans détailler les calculs, une valeur approchée au degré Celsius près de la moyenne de la
série.
3. Donner une interprétation de la médiane de cette série.
4. Pour cette question seulement, on considère la série des températures maximales atteintes à
Strasbourg le 25 juin de chaque année de 2010 à 2019. On sait que l’étendue des températures de
cette nouvelle série est égale à 18,5°C. Déterminer la température maximale atteinte à Strasbourg
le 25 juin 2019.
Les questions suivantes portent sur la série des températures maximales atteintes à Strasbourg le 25
juin de chaque année de 2010 à 2018.
5. On crée 9 fiches, une par année, sur lesquelles figure la température maximale atteinte le 25 juin
de l’année. On prend une fiche au hasard. Chacune des fiches a la même probabilité d’être tirée.
a. Quelle est la probabilité que la température écrite sur cette fiche soit égale à 26°C ?
b. Quelle est la probabilité que la température écrite sur cette fiche soit inférieure ou égale à
24°C ?
c. A-t-on raison de dire que l’on a plus de 40 % de chance de prendre une fiche sur laquelle la
température est supérieure à 25°C ?

Exercice 3 (17 points)
Sur la figure ci-dessous, qui n’est pas à l’échelle,

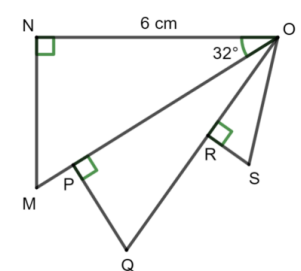
• le triangle ONM est rectangle en N,
• le triangle OPQ est rectangle en P,
• le triangle ORS est rectangle en R,
• ON = 6 cm et $\widehat{MON}= 32^{\circ}$ .
• P est un point du segment [OM] et R est un point du segment [OQ].
1. Calculer la mesure de la longueur MN. On donnera une valeur approchée au millimètre près.
2. On donne PQ = 2,5 cm et OQ = 6,5 cm. Montrer que OP = 6 cm.
3. Montrer que les triangles ONM et OPQ ne sont pas des triangles égaux.
4. Sachant que le triangle OPQ est un agrandissement du triangle ORS et que OS = 3,25 cm, calculer
l’aire du triangle ORS.

Exercice 4 (19 points)
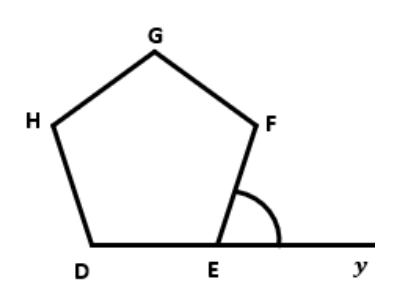
1. Sur la figure ci-dessous, DEFGH est un pentagone régulier et le point E appartient à la demi-droite
[Dy).

On admet que tous les angles du pentagone régulier mesurent 108 degrés.

Justifier que l’angle $\widehat{FEy}$ mesure 72 degrés.
2. Dans la suite de cet exercice, aucune justification n’est attendue.
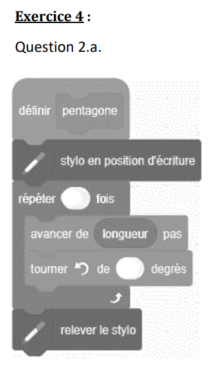
a. Compléter le bloc « pentagone » en ANNEXE, à rendre avec la copie, pour obtenir un
pentagone régulier. La variable « longueur » permet de modifier la longueur des côtés du
pentagone.

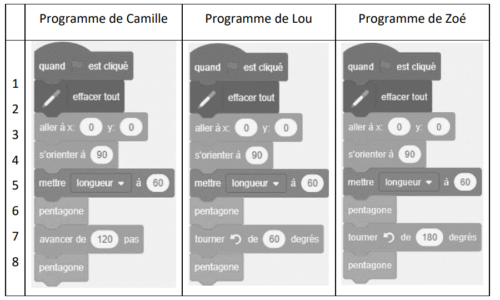
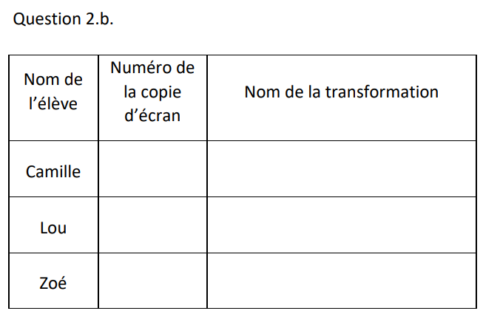
b. Camille, Lou et Zoé ont chacun codé un programme qui trace un pentagone et son image par
l’une des transformations suivantes : translation, symétrie centrale, rotation.

On rappelle que l’instruction « s’orienter à 90 » signifie que l’on s’oriente vers la droite.
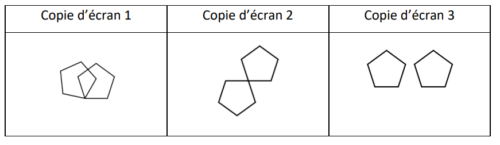
Les trois élèves ont effectué une copie d’écran de ce qu’ils ont obtenu sans indiquer ni leur
prénom ni le nom de la transformation choisie.

Compléter le tableau en ANNEXE, à rendre avec la copie, en associant le prénom de l’élève au numéro de sa copie d’écran ainsi qu’au nom de la transformation qu’il a choisie.
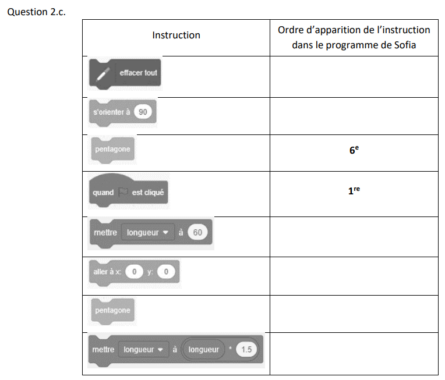
c. Sofia souhaite illustrer à l’aide d’un programme l’effet d’une homothétie sur un pentagone.

Le tableau en ANNEXE donne, dans le désordre, toutes les instructions utiles pour écrire ce
programme. L’ordre d’apparition dans le programme de deux instructions est précisé.
Compléter ce tableau sur l’ANNEXE, à rendre avec la copie, en indiquant l’ordre d’apparition de
chacune des instructions dans le programme de Sofia.

Exercice 5 (23 points)
La piscine du camping « le Rocher » dispose d’un bassin circulaire de forme cylindrique de rayon
3,60 m et de hauteur 1,50 m. En fin de saison, on utilise une pompe dont le débit est de 14, 1 pour vider l’eau de la piscine.
1. Montrer que le volume du bassin, arrondi au dixième de , est 61,1 .
2. Le bassin est plein. On met en route la pompe.

Au bout de 2 heures, quel volume d’eau en reste-t-il à vider ?

On considère la fonction : $V:t\mapsto 61,1- 0,235t$ .
3. a. Montrer que l’expression V(t) permet de déterminer le volume d’eau en qu’il reste à vider
dans le bassin en fonction de la durée , exprimée en minute, d’utilisation de la pompe.
b. Calculer le temps nécessaire pour que le volume d’eau restant à vider soit égal à 30 .
On donnera une valeur approchée à la minute près.
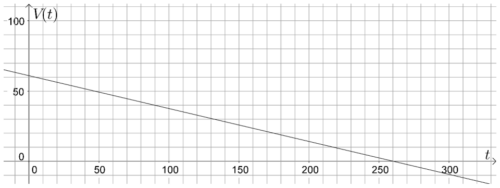
4. On a tracé ci-dessous une partie de la représentation graphique de la fonction V.

Répondre aux questions suivantes par une lecture graphique.
a. Déterminer l’antécédent de 40 par la fonction V . Interpréter le résultat.
b. Déterminer le temps nécessaire pour que la pompe vide complètement le bassin.

ANNEXE, à rendre avec la copie

Consulter le corrigé

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «brevet blanc de maths 2025 avec sujet et corrigé n°2.» au format PDF.