Asie Pacifique : brevet de maths 2024 avec sujet et corrigé en PDF.

Le sujet et le corrigé du brevet de maths 2024 en Asie Pacifique afin de permettre aux élèves de troisième de réviser le DNB en ligne. Ce sujet porte sur un QCM, un exercice sur un ensemble de cubes, un exercice de géométrie avec le théorème de Pythagore et de Thalès ainsi que, le calcul de l’aire d’un triangle. Des fonctions linéaires et affines avec un problème sur des amis qui se rendent en vacances. Un programme avec scratch qui trace des losanges et des polygones. Cette épreuve du DNB de maths en asie Pacifique 2024 dispose de sa correction au format PDF afin que les élèves de troisième puissent repérer leurs erreurs.

DIPLÔME NATIONAL DU BREVET
ASIE PACIFIQUE – SESSION 2024
MATHÉMATIQUES
Série générale
Durée de l’épreuve : 2 h 00 – 100 points

Exercice 1 : 20 points
Cet exercice est un questionnaire à choix multiples (QCM). Aucune justification n’est demandée. Pour chaque question, quatre réponses (A, B, C et D) sont proposées. Une seule réponse est
exacte. Recopier sur la copie le numéro de la question et la réponse.
Question 1
Lequel de ces quatre nombres est premier ?

Question 2
L’aire totale du patron d’un cube d’arête 5 cm est égale à…

Question 3
Une forme factorisée de l’expression littérale est…

Question 4
Un écran de télévision est au format 16 : 9 ce qui signifie que la longueur et la largeur de
l’écran sont dans le ratio 16 : 9.
Dans ce cas, si la longueur de l’écran est de 110 cm, sa largeur est d’environ …

Question 5
On considère la série de valeurs : $4,1\,\,-\,3,67\,\,-\,4,23\,-\,\,4,5\,-\,\,3,4$
Quelle est la médiane de cette série ?

Exercice 2 : 18 points
Voici trois affirmations. Pour chacune d’entre elles, justifier si elle est vraie ou fausse.
1. Voici un assemblage de quatre cubes identiques représenté en perspective cavalière.

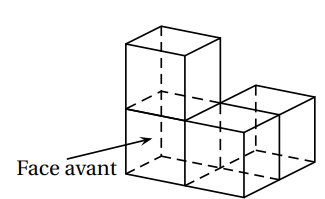
Affirmation n° 1 :
« La vue de droite est représentée par le dessin ci-dessous. »
Le dessin n’est pas à l’échelle.

2. On considère le schéma ci-dessous (qui n’est pas à l’échelle) :

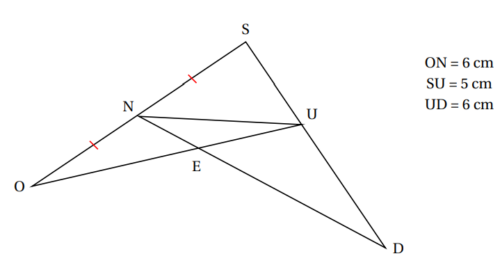
Affirmation n° 2 :

« Les droites (NU) et (OD) sont parallèles. »

3. On considère deux expériences aléatoires.
Dans la première expérience aléatoire, on tire une boule dans une urne opaque et on
annonce sa couleur.

Dans l’urne, il y a 4 boules rouges et 6 boules bleues indiscernables au toucher.
Dans la seconde expérience aléatoire, on lance un dé non truqué avec des faces numérotées de 1 à 6 et on annonce le nombre qui apparaît sur la face du dessus.

Affirmation n° 3 :

« La probabilité d’obtenir une boule bleue dans l’urne est supérieure à la probabilité d’obtenir un nombre pair avec le dé ».

Exercice 3 : 20 points
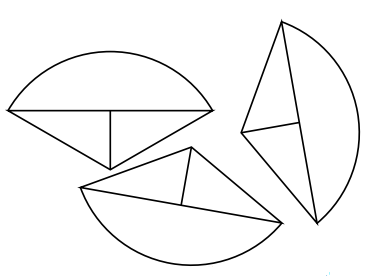
Trois élèves construisent chacun en vraie grandeur une même figure puis la découpent.
Ils obtiennent ainsi, à eux trois, trois pièces identiques, comme ci-dessous.

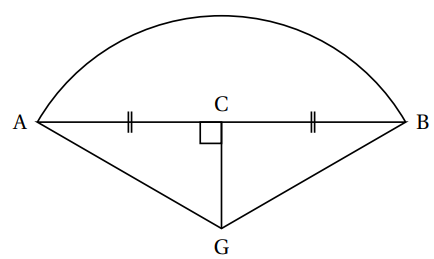
Le schéma ci-dessous représente la pièce construite par chaque élève avec les indications
suivantes :
• Les droites (AB) et (CG) sont perpendiculaires;
• Les points A, C et B sont alignés;
• L’arc de cercle qui relie le point A au point B a pour centre le point G;
• AC = CB;

• CG = 10 cm et BG = 20 cm.

1. Démontrer que la longueur BC mesure environ 17,3 cm.
2. Quelle est l’aire du triangle BAG ? On donnera une valeur arrondie à l’unité.
3. a. Montrer que l’angle $\widehat{CGB}$ mesure exactement 60°.
b. En déduire la mesure de l’angle $\widehat{AGB}$ .
4. Les trois élèves pensent qu’ils peuvent former un disque complet avec leurs 3 pièces.
Expliquer pourquoi ils ont raison.
5. En déduire l’aire de la pièce obtenue par chacun des élèves. On donnera une valeur
arrondie à l’unité.

Exercice 4 : 26 points
Des amis habitent Strasbourg et préparent leurs vacances.
Cette année ils ont décidé de partir découvrir une grande ville française pendant une semaine.
Pour s’y rendre, ils louent une voiture. Une fois arrivés sur place, ils feront ensuite tous leurs
trajets à pied ou en transport en commun.
Une agence de location de voitures propose les trois formules suivantes pour une location
sur une semaine :

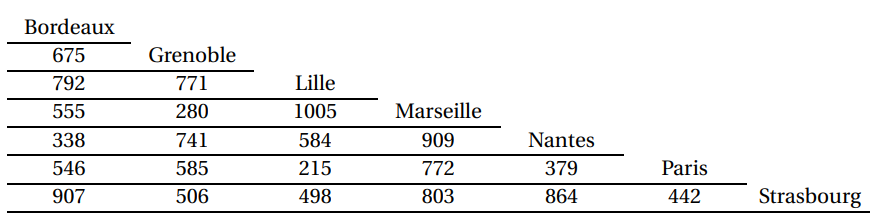
Tableau indicatif des distances (en km) entre des villes françaises.

Exemple : la distance la plus courte entre Nantes et Grenoble est de 741 km.

PARTIE A :

Les amis souhaitent se rendre à Marseille. Ils ont un budget de 1 000 € pour le voyage.

1. Quelle distance, en km, vont-ils parcourir pour le trajet aller-retour ?
2. En choisissant la formule B, montrer que la location de voiture coûtera 701,50 €.
3. Quelle est la formule la plus avantageuse ?
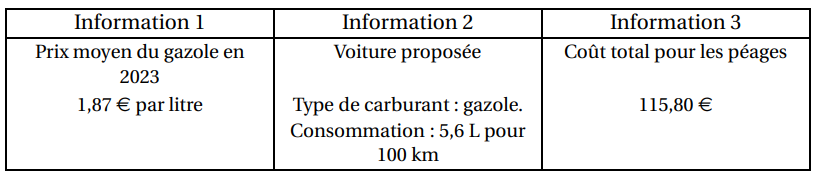
4. Voici des informations pour le voyage :

Leur budget sera-t-il suffisant ?
Dans cette question, toute trace de recherche sera prise en compte dans la correction.

PARTIE B : Étude des formules

5. Soit le nombre de kilomètres parcourus, exprimer en fonction de le prix payé pour
chaque formule de location.
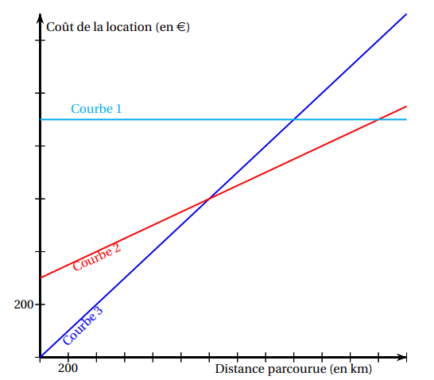
6. On a représenté ci-dessous, pour chacune des formules, le coût de la location (en euros) en fonction de la distance parcourue (en kilomètres).
Associer chaque courbe à la formule de location correspondante. Ne pas justifier.

7. Résoudre l’équation
$0,25x\,+300\,=\,0,5x.$
Interpréter ce résultat.

8. a. Si la distance parcourue est de 2 500 km, quelle formule doit-on choisir pour
payer le moins cher ? Ne pas justifier.
b. Donner une distance parcourue pour laquelle la formule A est la plus intéressante. Ne pas justifier.
c. Déterminer graphiquement quelle formule de location est la moins chère en fonction de la distance parcourue pour une distance inférieure à 2 600 km.

Exercice 5 : 16 points
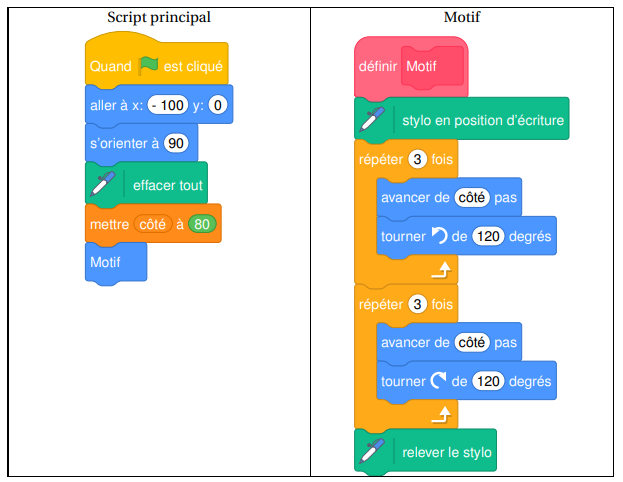
On donne le programme suivant.

Rappel :

Dans cet exercice, aucune justification n’est attendue.

1. À quelles coordonnées le lutin se positionne-t-il juste après avoir cliqué sur le drapeau
vert ?
2. En prenant 1 cm pour 20 pas, dessiner en vraie grandeur la figure obtenue en exécutant
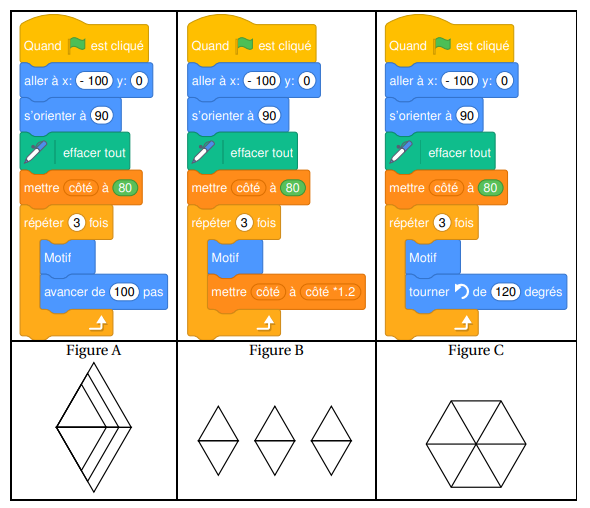
le script principal.
3. On modifie le script principal de trois façons différentes. Associer chaque script à la
figure qui lui correspond.

4. Dans cette question on s’intéresse au script n° 2.
a. Combien de fois le bloc « motif » est-il exécuté ?
b. Quelle est la valeur de la variable « côté » à la fin de ce script ?

Consulter le corrigé en ligne

4.9/5 - (7 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «asie Pacifique : brevet de maths 2024 avec sujet et corrigé en PDF.» au format PDF.

D'autres fiches similaires :

Mathovore c'est 13 984 044 cours et exercices de maths téléchargés en PDF.