La dérivée d’une fonction : cours de maths en terminale en PDF.
I. La notion de dérivée d’une fonction
1.Dérivabilité et fonction dérivée
On considère une fonction f définie sur un intervalle I de ainsi que deux nombres réels
et
tel que
et
appartiennent à I.
La fonction f est dérivable en a si et seulement si avec
.
Si c’est le cas, le réel est appelé le nombre dérivée de f en a et se note
.
On considère une fonction f définie sur un intervalle I de .La fonction f est dérivable sur I si elle est dérivable en tout
de I.
La fonction définie sur I est appelée la fonction dérivée de f sur l’intervalle I.
2.Applications à la dérivation
On considère une fonction f dérivable en et
sa courbe dans un repère orthonormé du plan.Une équation de la tangente à la courbe
au point d’abscisse
est :
.
On considère une fonction f définie et dérivable sur un intervalle I de .
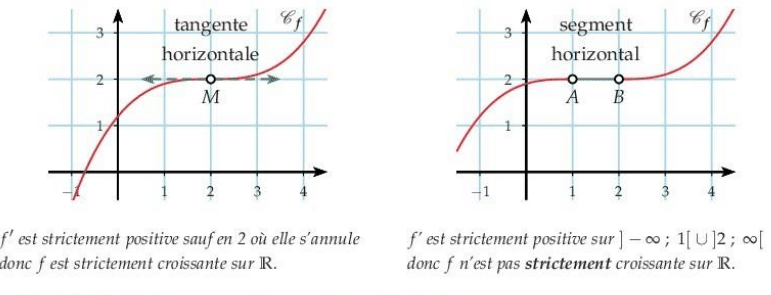
- Si
est strictement positive sur I alors f est strictement croissante sur I;
- Si
est strictement négative sur I alors f est strictement décroissante sur I;
- Si
est nulle sur I alors f est constante sur I.
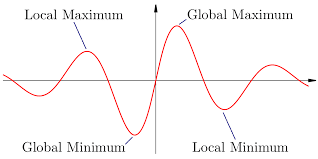
On considère une fonction f définie et dérivable sur un intervalle I de et
.Si
admet un extremum local en
alors
.
Si s’annule et change de signe en
alors
admet un extremum local en
.
3.Calculs de dérivées
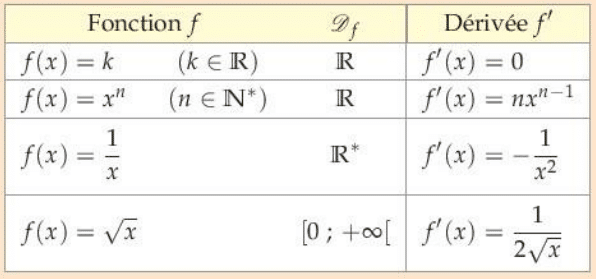
On note le domaine de définition de la fonction f.Toutes les fonctions du tableau ci-dessous sont dérivables sur
à l’exception de la fonction racine carrée qui n’est pas dérivable en
.
On considère un nombre réel k et deux fonctions u et v dérivables sur un intervalle I.Les fonction u+v, ku et uv sont dérivables sur I;
Les fonctions et
sont dérivables sur I sauf là où
s’annule.
II.Dérivées des fonctions composées
- Si la fonction
est dérivable et strictement positive sur I alors
est dérivable sur I.
- Si c’est le cas, nous avons :
.
Soit n un entier naturel non nul.Si est dérivable sur I alors :
- La fonction
est dérivable sur I et
.
- La fonction
est dérivable sur I sauf là où u s’annule et
.
On considère deux nombres réels a et b.Si est dérivable sur I alors :
La fonction est dérivable là où
.
Si c’est le cas , .
Soit une fonction dérivable sur I et f une fonction dérivable sur un intervalle J telle que :Pour tout
.
La fonction composée de u suivie de f est dérivable sur I, et pour tout
:
ou encore
.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «la dérivée d’une fonction : cours de maths en terminale en PDF.» au format PDF.
D'autres cours et exercices à consulter
- Matrices et opérations : cours de maths en terminale spécialité en PDF.
- Arithmétique : cours de maths en terminale spécialité en PDF.
- Les suites numériques : cours de maths en terminale en PDF.
- Les limites et les asymptotes : cours de maths en terminale en PDF.
- Les probabilités conditionnelles : cours de maths en terminale en PDF.
- La fonction logarithme népérien : cours de maths en terminale en PDF.
- Géométrie dans l’espace : cours de maths en terminale en PDF.
- Le raisonnement par récurrence : cours de maths en terminale en PDF.