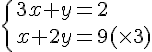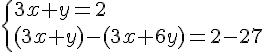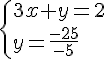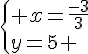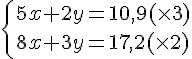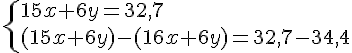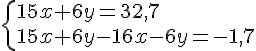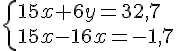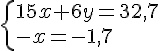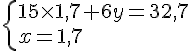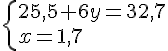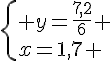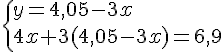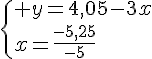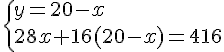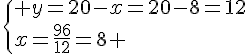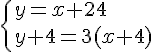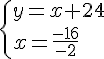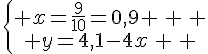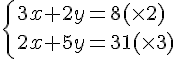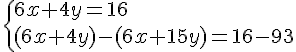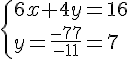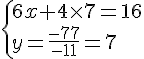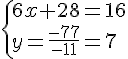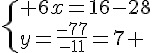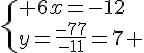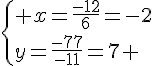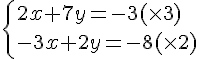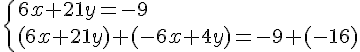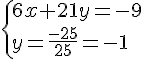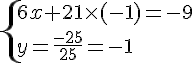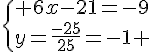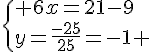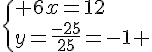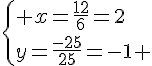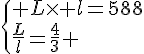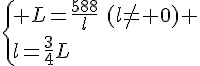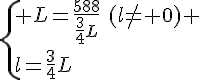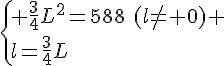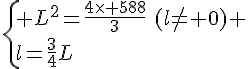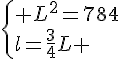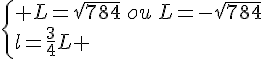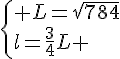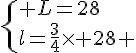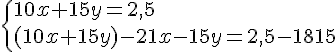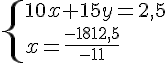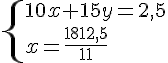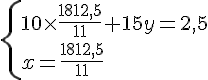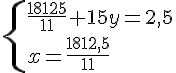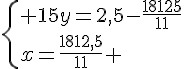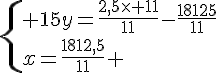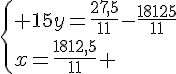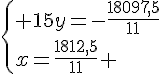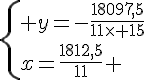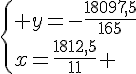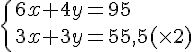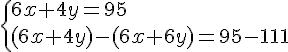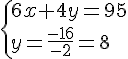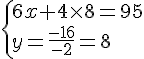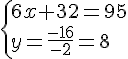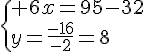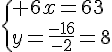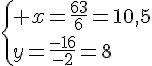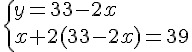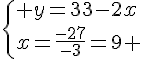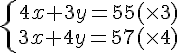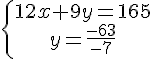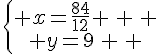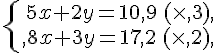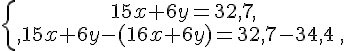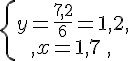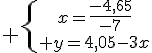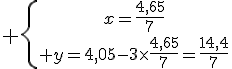Systèmes équations : corrigé des exercices de maths en 2de.

Mis à jour le 29 mai 2025

🔍Corrigés Détaillés

2de • Scolaire

Systèmes équations

🔎 Analyse : 16 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en 2de sur les systèmes d’équations à deux inconnues. Résoudre avec la méthode par combinaison linéaire ou par substitution.

Exercice 1 :

Nous obtenons le système suivant :

Elle peut prendre les différentes possibilités suivantes :

– 3 lots de guppys et lot de néons : 30 + 5×4=50 cm

– 2 lots de guppys et 3 lots de néons ; 20 + 3x5x4=80 cm

– 1 lot de guppy et 4 lots de néons ; 10+4x5x4= 90 cm

– o lot de guppy et 6 lots de néons ; 6x5x4=120 cm

Conclusion : elle pourra soit mettre 3 lots de guppys et un lot de néonsou

2 lots de guppys et 3 lots de néons.

Exercice 2 :

Notons x le premier nombre et y le second nombre, nous obtenons le système suivant :

$\{ 3x+y=2\\x+2y=9 .$

$\{ 3x+y=2\\x+2y=9(\times 3) .$

$\{ 3x+y=2\\3x+6y=27 .$

$\{ 3x+y=2\\(3x+y)-(3x+6y)=2-27 .$

$\{ 3x+y=2\\3x+y-3x-6y=-25 .$

$\{ 3x+y=2\\y-6y=-25 .$

$\{ 3x+y=2\\-5y=-25 .$

$\{ 3x+y=2\\y=\frac{-25}{-5} .$

$\{ 3x+y=2\\y=5 .$

$\{ 3x+5=2\\y=5 .$

$\{ 3x=-3\\y=5 .$

$\{ x=\frac{-3}{3}\\y=5 .$

$\{ x=-1\\y=5 .$

Conclusion : les deux nombres choisis sont – 1 et 5 .

Exercice 3 :

Soit f cette fonction affine,

nous avons f(3)=17 et f(7)=33.

$a=\frac{f(7)-f(3)}{7-3}=\frac{33-17}{7-3}=\frac{16}{4}=4$

$b=f(3)-a\times 3=17-4\times 3=17-12=5$

donc la fonction affine est

f(x)=4x+5

Résolvons les équations suivantes :

f(x)=37

4x+5=37

4x=37-5

4x=32

x=32:4

x=8

f(x)=9

4x+5=9

4x=9-5

4x=4

x=4:4

x=1

f(x)=17

4x+5=17

4x=17-5

4x=12

x=12:4

x=3

f(x)=29

4x+5=29

4x=29-5

4x=24

x=24:4

x=6

Conclusion : le code de la carte bancaire est 8136 .

Exercice 4 :

Retrouvez le prix de chaque article.

Soit x le prix d’un crayon et y le prix d’une gomme.

Nous obtenons le système suivant :

$\{ 5x+2y=10,9\\8x+3y=17,2 .$

$\{ 5x+2y=10,9 (\times 3)\\8x+3y=17,2 (\times 2).$

$\{ 15x+6y=32,7 \\16x+6y=34,4 .$

$\{ 15x+6y=32,7 \\(15x+6y)-(16x+6y)=32,7-34,4 .$

$\{ 15x+6y=32,7 \\15x+6y-16x-6y=-1,7 .$

$\{ 15x+6y=32,7 \\15x-16x=-1,7 .$

$\{ 15x+6y=32,7 \\-x=-1,7 .$

$\{ 15\times 1,7+6y=32,7 \\x=1,7 .$

$\{ 25,5+6y=32,7 \\x=1,7 .$

$\{ 6y=32,7-25,5 \\x=1,7 .$

$\{ 6y=7,2 \\x=1,7 .$

$\{ y=\frac{7,2}{6} \\x=1,7 .$

$\{ y=1,2 \\x=1,7 .$

Conclusion :

le prix d’un crayon de papier est de 1,4 euro et le prix d’une gomme est de 1,2 euro .

Exercice 5 :

Notons x le prix d’un croissant et y le prix d’un pain au lait.

Nous obtenons le système d’équations suivant :

$\{ 3x+y=4,05\\4x+3y=6,9 .$

$\{ y=4,05-3x\\4x+3(4,05-3x)=6,9 .$

$\{ y=4,05-3x\\4x+12,15-9x=6,9 .$

$\{ y=4,05-3x\\12,15-5x=6,9 .$

$\{ y=4,05-3x\\-5x=6,9- 12,15.$

$\{ y=4,05-3x\\-5x=-5,25.$

$\{ y=4,05-3x\\x=\frac{-5,25}{-5}.$

$\{ y=4,05-3x\\x=1,05.$

$\{ y=4,05-3\times 1,05\\x=1,05.$

$\{ y=0,9\\x=1,05.$

Conclusion : le prix d’un croissant est de 1,05 euro et le prix d’un pain au lait est de 0,90 euro.

Exercice 6 :

Un camion transporte 20 caisses de masses différentes:

les unes pèsent 28 kg, les autres 16 kg.

Sachant que la masse totale de ces caisses est 416 kg .

Combien y a t-il de caisses de chaque catégorie ?

Notons x le nombre de caisses de 28 kg et y le nombre de caisses de 16 kg .

$\{ x+y=20\\28x+16y=416 .$

$\{ y=20-x\\28x+16(20-x)=416 .$

$\{ y=20-x\\28x+16\times 20-16x=416 .$

$\{ y=20-x\\12x+320=416 .$

$\{ y=20-x\\12x=416-320 .$

$\{ y=20-x\\12x=96 .$

$\{ y=20-x=20-8=12\\x=\frac{96}{12}=8 .$

Conclusion :

Ce camion contient 8 caisses de 28 kg et 12 caisses de 16 kg .

Exercice 7 :

Combien de chaque espèce d’oiseau Betty a acheté ?
Il y a en fait que deux équations et trois inconnues.
Mais le fait que les inconnues soient entières te permet de résoudre le système quand même.

P osons x le nombre de canards, y le nombre de poulets et z le nombre de poussins.

Betty achète 100 oiseaux, donc : x+y+z=100
Pour 100€ , donc : $5x+y+\frac{z}{20}=100$

De la première équation : .

On remplace dans la deuxième, pour obtenir la relation :

$5(100-y-z)+y+\frac{z}{20}=100$

$500-5y-5z+y+\frac{z}{20}=100$

$500-4y-\frac{100}{20}z+\frac{z}{20}=100$

$-4y-\frac{99}{20}z=100-500$

$-4y=-400+\frac{99}{20}z$

$y=\frac{-400}{-4}+\frac{99}{-4\times 20}z$

$y=100-\frac{99}{80}z$

$y=\frac{8000-99z}{80}$

Et c’est maintenant qu’il faut utiliser les entiers !
D’après l’énoncé, Betty achète les poussins par groupe de 20.
Elle achète donc 20, 40, 60 ou 80 poussins (0 est impossible car elle achète au moins un poussin, et 100 aussi car sinon elle n’aurait acheté que des poussins, et donc pas « au moins un canard et un poulet »).

Et tu trouves :
– pour z=20, y=75.25 (impossible car pas entier)
– pour z=40, y=50.5 (impossible car pas entier)
– pour z=60, y=25.75 (impossible car pas entier)
– pour z=80, y=1

La seule solution entière est donc y=1, z=80. Et x=100-y-z=19.

Betty a donc acheté 19 canards, 1 poulet, et 4 lots de 20 (soit 80) poussins.

Exercice 8 :

Une mère a 24ans de plus que sa fille.

Dans 4 ans sont âge sera le triple de celui de sa fille.
Quelle est l’âge de la fille?

Quelle est l’âge de la Mère?

Soit x : l’âge de la fille et y l’âge de la mère .

$\{ y=x+24\\y+4=3(x+4) .$

$\{ y=x+24\\x+24+4=3x+12 .$

$\{ y=x+24\\x+28-3x=12 .$

$\{ y=x+24\\-2x=12-28 .$

$\{ y=x+24\\-2x=-16 .$

$\{ y=x+24\\x=\frac{-16}{-2} .$

$\{ y=8+24\\x=8 .$

$\{ y=32\\x=8 .$

Conclusion : la mère a 32 ans et la fille a 8 ans .

Exercice 9 :

1. Écrire les équations qui traduisent le texte.

Notons x le prix d’un CD et y le prix d’une BD.

$\{\begin{matrix} 2x+3y=3,3 \, \, \\ 4x+y=4,1\, \, \end{matrix}.$

2.Résoudre le système d’équations et donner le prix d’un CD et le prix d’une BD.

$\begin{matrix} 2x+3y=3,3 \, \, \\ y=4,1-4x\, \, \end{matrix}.$

$\{\begin{matrix} 2x+3(4,1-4x)=3,3 \, \, \\ y=4,1-4x\, \, \end{matrix}.$

$\{\begin{matrix} 2x+12,3-12x=3,3 \, \, \\ y=4,1-4x\, \, \end{matrix}.$

$\{\begin{matrix} -10x+12,3=3,3 \, \, \\ y=4,1-4x\, \, \end{matrix}.$

$\{\begin{matrix} -10x=3,3-12,3 \, \, \\ y=4,1-4x\, \, \end{matrix}.$

$\{\begin{matrix} -10x=-9 \, \, \\ y=4,1-4x\, \, \end{matrix}.$

$\{\begin{matrix} x=\frac{9}{10}=0,9 \, \, \\ y=4,1-4x\, \, \end{matrix}.$

$\{\begin{matrix} x=0,9 \, \, \\ y=4,1-4\times 0,9=4,1-3,6\, \, \end{matrix}.$

$\{\begin{matrix} x=0,9 \, \, \\ y=0,5\, \, \end{matrix}.$

Le prix d’un CD est de 0,90 € et le prix 0,50 €

3.Un mois plus tard, le magasin propose une réduction de 10 % sur les CD et 15 % sur les BD.

Combien aurait alors payé Loïc ?

Pour une réduction de 10%, le coefficient est 0,9 et pour une réduction de 15%, le coefficient est de 0,85.

Le prix d’un Cd devient 0,9×0,9=0,81€

Le prix d’un DVD serait 0,5×0,85=0,425 €

0,81×2+0,425×3=1,62+1,275=2,895 €

Loïc paiera donc 2,895 euros.

Exercice 10 :

Système n° 1 :

$\{ 3x+2y=8\\2x+5y=31 .$

$\{ 3x+2y=8(\times 2)\\2x+5y=31 (\times 3).$

$\{ 6x+4y=16\\6x+15y=93 .$

$\{ 6x+4y=16\\(6x+4y)-(6x+15y)=16-93 .$

$\{ 6x+4y=16\\6x+4y-6x-15y=-77 .$

$\{ 6x+4y=16\\-11y=-77 .$

$\{ 6x+4y=16\\y=\frac{-77}{-11}=7 .$

$\{ 6x+4\times 7=16\\y=\frac{-77}{-11}=7 .$

$\{ 6x+28=16\\y=\frac{-77}{-11}=7 .$

$\{ 6x=16-28\\y=\frac{-77}{-11}=7 .$

$\{ 6x=-12\\y=\frac{-77}{-11}=7 .$

$\{ x=\frac{-12}{6}=-2\\y=\frac{-77}{-11}=7 .$

Conclusion : ${\color{DarkRed} S= \{ (-2;7) \}}$

Système n° 2 :

$\{ 2x+7y=-3\\-3x+2y=-8 .$

$\{ 2x+7y=-3(\times 3)\\-3x+2y=-8(\times 2) .$

$\{ 6x+21y=-9\\-6x+4y=-16 .$

$\{ 6x+21y=-9\\(6x+21y)+(-6x+4y)=-9+(-16) .$

$\{ 6x+21y=-9\\6x+21y-6x+4y=-9-16 .$

$\{ 6x+21y=-9\\21y+4y=-25 .$

$\{ 6x+21y=-9\\25y=-25 .$

$\{ 6x+21y=-9\\y=\frac{-25}{25}=-1 .$

$\{ 6x+21\times (-1)=-9\\y=\frac{-25}{25}=-1 .$

$\{ 6x-21=-9\\y=\frac{-25}{25}=-1 .$

$\{ 6x=21-9\\y=\frac{-25}{25}=-1 .$

$\{ 6x=12\\y=\frac{-25}{25}=-1 .$

$\{ x=\frac{12}{6}=2\\y=\frac{-25}{25}=-1 .$

Conclusion : ${\color{DarkRed} S= \{ (2;-1) \}}$ .

Exercice 11 :

Résoudre le système suivant :

$\{ x+3y=10\\ 3x-y=0 .$

$\{ x=10-3y\\3(10-3y)-y=0 .$

$\{ x=10-3y\\30-9y-y=0 .$

$\{ x=10-3y\\30-10y=0 .$

$\{ x=10-3y\\-10y=-30 .$

$\{ x=10-3y\\y=3 .$

$\{ x=10-3\times 3\\y=3 .$

$\{ x=1\\y=3 .$

Exercice 12 :

Calculer la longueur L et la largeur l .

$\{ L\times l=588\\\frac{L}{l}=\frac{4}{3} .$

$\{ L=\frac{588}{l}\,\,(l\neq 0) \\l=\frac{3}{4}L.$

$\{ L=\frac{588}{\frac{3}{4}L}\,\,(l\neq 0) \\l=\frac{3}{4}L.$

$\{ \frac{3}{4}L^2=588\,\,(l\neq 0) \\l=\frac{3}{4}L.$

$\{ L^2=\frac{4\times 588}{3}\,\,(l\neq 0) \\l=\frac{3}{4}L.$

$\{ L^2=784\\l=\frac{3}{4}L .$

$\{ L=\sqrt{784}\,ou\,L=-\sqrt{784}\\l=\frac{3}{4}L .$

Or L est une longueur donc c’est un nombre positif .

$\{ L=\sqrt{784}\\l=\frac{3}{4}L .$

$\{ L=28\\l=\frac{3}{4}\times 28 .$

$\{ L=28\\l=21 .$

Exercice 13 :

$\{ 2x+3y=0,5\\7x+5y=605 .$

$\{ 2x+3y=0,5\,\,\times 5\\7x+5y=605\,\,\times 3 .$

$\{ 10x+15y=2,5\\21x+15y=1815 .$

$\{ 10x+15y=2,5\\(10x+15y)-21x-15y=2,5-1815 .$

$\{ 10x+15y=2,5\\10x+15y-21x-15y=-1812,5 .$

$\{ 10x+15y=2,5\\-11x=-1812,5 .$

$\{ 10x+15y=2,5\\x=\frac{-1812,5}{-11} .$

$\{ 10x+15y=2,5\\x=\frac{1812,5}{11} .$

$\{ 10\times \frac{1812,5}{11}+15y=2,5\\x=\frac{1812,5}{11} .$

$\{ \frac{18125}{11}+15y=2,5\\x=\frac{1812,5}{11} .$

$\{ 15y=2,5-\frac{18125}{11}\\x=\frac{1812,5}{11} .$

$\{ 15y=\frac{2,5\times 11}{11}-\frac{18125}{11}\\x=\frac{1812,5}{11} .$

$\{ 15y=\frac{27,5}{11}-\frac{18125}{11}\\x=\frac{1812,5}{11} .$

$\{ 15y=-\frac{18097,5}{11}\\x=\frac{1812,5}{11} .$

$\{ y=-\frac{18097,5}{11\times 15}\\x=\frac{1812,5}{11} .$

$\{ y=-\frac{18097,5}{165}\\x=\frac{1812,5}{11} .$

Exercice 14 :

Quel est le prix du kilogramme de vernis et du litre de cire ?

Soit x : le prix d’un kilogramme de vernis en euro et y : le prix d’un litre de cire en euro.

Nous obtenons le système suivant :

$\{ 6x+4y=95\\3x+3y=55,5 .$

$\{ 6x+4y=95\\3x+3y=55,5 (\times 2).$

$\{ 6x+4y=95\\6x+6y=111 .$

$\{ 6x+4y=95\\(6x+4y)-(6x+6y)=95-111 .$

$\{ 6x+4y=95\\6x+4y-6x-6y=-16.$

$\{ 6x+4y=95\\-2y=-16.$

$\{ 6x+4y=95\\y=\frac{-16}{-2}=8.$

$\{ 6x+4\times 8=95\\y=\frac{-16}{-2}=8.$

$\{ 6x+32=95\\y=\frac{-16}{-2}=8.$

$\{ 6x=95-32\\y=\frac{-16}{-2}=8.$

$\{ 6x=63\\y=\frac{-16}{-2}=8.$

$\{ x=\frac{63}{6}=10,5\\y=\frac{-16}{-2}=8.$

Conclusion : un kilogramme de vernis coûte 10,50 euros et un litre de cire coûte 8 euros.

Exercice 15 :

Soit la note du contrôle et la note du devoir maison.

$\{ 2x+y=33\\x+2y=39 .$

$\{ y=33-2x\\x+2(33-2x)=39 .$

$\{ y=33-2x\\x+66-4x=39 .$

$\{ y=33-2x\\-3x=39-66 .$

$\{ y=33-2x\\-3x=-27 .$

$\{ y=33-2x\\x=\frac{-27}{-3}=9 .$

$\{ y=33-2\times 9=33-18=15\\x=9.$

Conclusion : Ahmed a obtenu 9 au contrôle et 15 au devoir maison .

Exercice 16 :

1) On désire calculer le débit, en litre par heures, de chacune des fontaines.

Pour cela, on admet que les renseignements précédents sont traduits par le système de deux équations à deux inconnues :

$\{{4x+3y=55\atop 3x+4y=57}$

où x est le débit horaire de la première fontaine et y est le débit horaire de la seconde fontaine.

Résoudre le système et indiquer le débit horaire de chacune des

deux fontaines.

$\{\begin{matrix} 4x+3y=55(\times 3) \, \, \\ 3x+4y=57(\times 4)\, \, \end{matrix}.$

$\{\begin{matrix} 12x+9y=165 \, \, \\ 12x+16y=228\, \, \end{matrix}.$

$\{\begin{matrix} 12x+9y=165 \, \, \\ 12x+9y-(12x+16y)=165-228\, \, \end{matrix}.$

$\{\begin{matrix} 12x+9y=165 \, \, \\ 12x+9y-12x-16y=-63\, \, \end{matrix}.$

$\{\begin{matrix} 12x+9y=165 \, \, \\ -7y=-63\, \, \end{matrix}.$

$\{\begin{matrix} 12x+9y=165 \, \, \\ y=\frac{-63}{-7}\, \, \end{matrix}.$

$\{\begin{matrix} 12x+9y=165 \, \, \\ y=9\, \, \end{matrix}.$

$\{\begin{matrix} 12x+9\times 9=165 \, \, \\ y=9\, \, \end{matrix}.$

$\{\begin{matrix} 12x+81=165 \, \, \\ y=9\, \, \end{matrix}.$

$\{\begin{matrix} 12x=165-81 \, \, \\ y=9\, \, \end{matrix}.$

$\{\begin{matrix} 12x=84 \, \, \\ y=9\, \, \end{matrix}.$

$\{\begin{matrix} x=\frac{84}{12} \, \, \\ y=9\, \, \end{matrix}.$

$\{\begin{matrix} x=7\, \, \\ y=9\, \, \end{matrix}.$

Le débit horaire de la première fontaine est de 7 litres et celui de la seconde est de 9 litres.

2) Sachant que ce bassin peut contenir 320 litres, combien faudra-t-il de temps pour le remplir, si les deux fontaines coulent ensemble pendant le même temps ?

Chaque heure il y aura 16 litres d’écoulé.

320:16 = 20

Il faudra donc 20 heures pour que ce bassin soit rempli.

Exercice 17 :
Soit le nombre de dromadaires et le nombre de chameaux .
Il y a 19 bonnets et un chameau a 2 bosses :
Il y a 24 paires de pantoufles, chaque camélidé a 4 pattes donc 2 paires de pantoufles :
On est amené à résoudre le système suivant :
$\{\begin{matrix}\,x+y=12\,\,\\,x+2y=19\,\,\end{matrix}.$
$\{\begin{matrix}\,x+y=12\,\,\\,(x+2y)-(x+y)=19-12\,\,\end{matrix}.$
$\{\begin{matrix}\,x+y=12\,\,\\,x+2y-x-y=7\,\,\end{matrix}.$
$\{\begin{matrix}\,x+y=12\,\,\\,y=7\,\,\end{matrix}.$
$\{\begin{matrix}\,x+7=12\,\,\\,y=7\,\,\end{matrix}.$
$\{\begin{matrix}\,x=12-7\,\,\\,y=7\,\,\end{matrix}.$
$\{\begin{matrix}\,x=5\,\,\\,y=7\,\,\end{matrix}.$
Conclusion : il y a 5 dromadaires et 7 chameaux .

Exercice 18 :

$\{\begin{matrix}\,5x+2y=10,9\,(\times ,3),\,\,\\,8x+3y=17,2\,(\times ,2),\,\,\end{matrix}.$

$\{\begin{matrix}\,15x+6y=32,7,\,\,\\,16x+6y=34,4\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,15x+6y=32,7,\,\,\\,15x+6y-(16x+6y)=32,7-34,4\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,15x+6y=32,7,\,\,\\,15x+6y-16x-6y=-1,7\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,15x+6y=32,7,\,\,\\,-x=-1,7\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,15x+6y=32,7,\,\,\\,x=1,7\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,15\times ,1,7+6y=32,7,\,\,\\,x=1,7\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,25,5+6y=32,7,\,\,\\,x=1,7\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,6y=32,7-25,5,\,\,\\,x=1,7\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,6y=7,2,\,\,\\,x=1,7\,,\,\,\end{matrix}.$

$\{\begin{matrix}\,y=\frac{7,2}{6}=1,2,\,\,\\,x=1,7\,,\,\,\end{matrix}.$

2)Notons x le nombre de crayons et y le nombre de gommes.

Nous obtenons le système précédent après traduction de l’énoncé.

Conclusion : le prix d’un crayon est de 1,20 € et le prix d’une gomme est de 1,7 €.

Exercice 19 :

Exercice 20 :

Exercice 21 :

Notons x: le nombre d’autos
et y: le nombre de motos.

Traduction mathématiques :
Il y a en tout 65 véhicules donc x+y = 65
On dénombre 180 roues donc 4x+2y = 180
car une auto possède 4 roues et une moto en possède 2.
Le problème revient à résoudre le système suivant :

Conclusion : il y a 25 autos et 40 motos.
Exercice 22 :
$\{{2x+3y=5,5\atop 3x+y=4,05}$ .

1. Le couple (x=2;y=0,5) est-il solution de ce système ?.

$\{{2\times 2+3\times 0,5=5,5\atop 3\times 2+0,5=6,5}$

donc ce couple n’est pas solution du système.

2. Résoudre ce système d’équations .

$\{{2x+3y=5,5\atop 3x+y=4,05}$

$\{{2x+3y=5,5\atop y=4,05-3x}$

$\{{2x+3(4,05-3x)=5,5\atop y=4,05-3x}$

$\{{2x+12,15-9x=5,5\atop y=4,05-3x}$

$\{{-7x=-12,15+5,5\atop y=4,05-3x}$

$\{{-7x=-4,65\atop y=4,05-3x}$

$\{{x=\frac{-4,65}{-7}\atop y=4,05-3x}$

$\{{x=\frac{4,65}{7}\atop y=4,05-3\times \frac{4,65}{7}=\frac{14,4}{7}}$

3. A la boulangerie, Anatole achète 2 croissants et 3 pains au chocolat : il paie 5,50.

Béatrice achète 3 croissants et 1 pain au chocolat et paie 4,05 .

Quel est le prix d’un croissant? Quel est le prix d’un pain au chocolat ?

En notant x: le prix d’un croissant et y : le prix d’un pain au chocolat, on aboutit au système précédent.

4.5/5 - (28096 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «systèmes équations : corrigé des exercices de maths en 2de.» au format PDF.

Ressources de seconde

Cours de seconde

Généralités sur les fonctions et fonctions usuelles

Factorisation et étude de signe

Racine carrée

Généralités sur les fonctions numériques

Variations de fonctions et extremums

Nombres entiers et rationnels et calcul du PGCD

Exercices de seconde

Fonctions

Vecteurs et translation

Racine carrée

Géométrie dans l’espace

Systèmes de deux équations

Probabilités

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.

Systèmes équations : corrigé des exercices de maths en 2de.

Ressources de seconde

Cours de seconde

Exercices de seconde

L'équipe Mathovore

12 Enseignants Titulaires

Nos ressources pédagogiques