La géométrie dans l’espace et le calcul de volumes à travers des exercices de maths 2de corrigés. L’élève devra savoir représenter l’intersection d’un plan ou d’une droite avec un solide de l’espace.
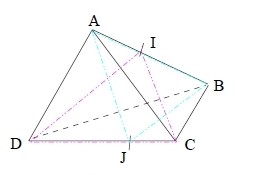
Exercice 1 – Tétraèdre et intersection de plan
Dans un tétraèdre ABCD, I est un point de l’arête [AB], J un point de l’arête [CD].
Le but de l’exercice est de trouver l’intersection des plans (AJB) et (CID).
1. Prouver que chacun des points I et J appartient à la fois aux plans (AJB) et (CID).
2. Quelle est alors l’intersection de ces deux plans.
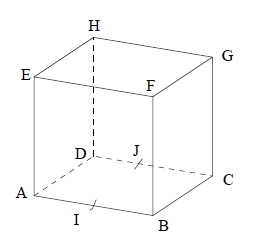
Exercice 2 – Cube et plan de l’espace
ABCDEFGH est un cube. I est le milieu de [AB].
J est le milieu de [CD].
Quel est dans chacun des cas suivants, l’intersection des deux plans ?
Justifier chaque réponse.
1. Le plan (AIE) et le plan (BIG).
2. Le plan (ADI) et le plan (BJC).
3. Le plan (HEF) et le plan (BJC).
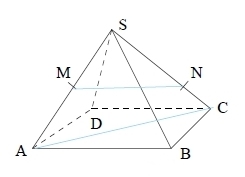
Exercice 3 – Pyramide régulière et droites
SABCD est une pyramide régulière à base carrée.
M est le milieu de [SA], N est le point de [SC] tel que .
1. Démontrer que les droites (MN) et (AC) sont sécantes.
2. Placer le point d’intersection de (MN) et (AC).
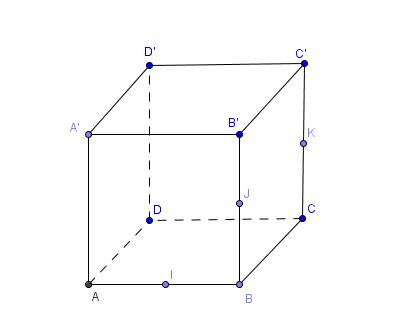
Exercice 4 – Cube
Les points I, J et K sont des milieux.
Dire si les affirmations sont vraies ou fausses et démontrer.
1) (IJ) et (A’D’) sont parallèles .
2) (AJ) et (DK) sont parallèles .
Exercice 5 – Volume d’une pyramide
La pyramide ci-dessous à pour base un rectangle ABCD de périmètre 24 cm et pour hauteur le segment [SA] de longueur triple de celle du segment [AB].
On pose AB=x.
1. Quelles valeurs peut prendre x
2. Démontrer que le volume de la pyramide SABCD est donné par la formule: V=x²(12-x)
3. Quelle est le volume de la pyramide lorsque ABCD est un carré ?
Exercice 6
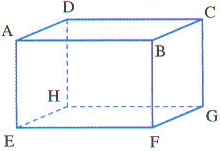
ABCDEFGH est un parallélépipède rectangle. Chaque réponse devra être justifiée.
1. les droites (AD) et (EF) sont-elles sécantes ?
2. Les droites (AE) et (CG) sont-elles parallèles ?
3. Les points A, E, C, G sont-ils coplanaires ?
4.Les droites (AD) et le plan (EGH) sont-ils sécants ?
5. Les plans (BCD) et (AEH) sont-ils sécants ?
Exercice 7
Les points A,B,R,U appartiennent au plan ;
les points S et T n’appartiennent pas à .
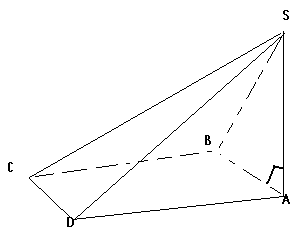
SAB est un triangle isocèle en S et RSUT est un losange de centre, le milieu O de [AB].
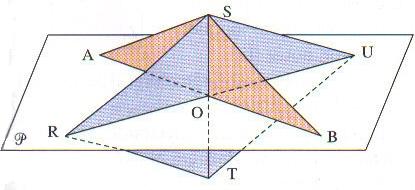
Démontrer que la droite (SO) est orthogonale au plan .
Exercice 8
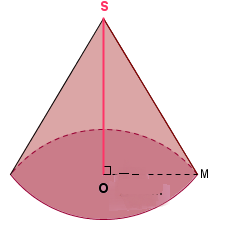
En faisant tourner le triangle AHS, rectangle en H, autour de (SH), on obtient le cône de révolution représenté ci-dessous.
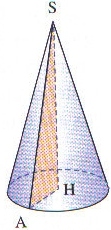
On sait que AS = 10 cm et
1. Calculer l’arrondi au dixième du rayon r, en cm, du cercle de base.
2. Calculer l’arrondi au dixième de la hauteur h, en cm, du cône .
3.Calculer l’arrondi au cm² de l’aire latérale du cône .
Exercice 9
ABCDEFGH est un cube d’arête 5 cm.
I est le milieu de l’arête [EF].
Le but de cet exercice est le calcul du volume de la pyramide IABGH, et celui de la longueur de sa hauteur, notée [IS].
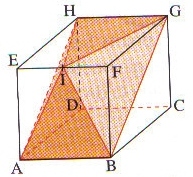
1. Calculer les volumes des tétraèdres IFBG et IEAH et le volume du prisme ADHBCG .
2.En déduire le volume de la pyramide IABGH.
3. Calculer l’aire du quadrilatère ABGH, et en déduire la hauteur IS de cette pyramide .
4.Reproduire cette figure et tracer la hauteur [IS] .
Exercice 10 – Sphère et pyramide
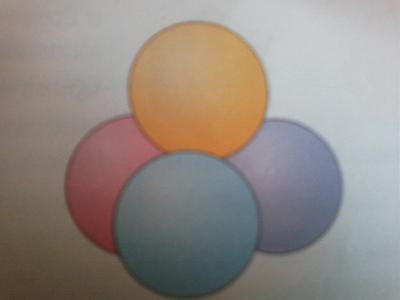
Quatre ballons sphériques de diamètre 20 cm sont disposés de façon a former une pyramide.
Quelle est la hauteur de la pyramide ?
Exercice 12 – Cône de révolution et chapeau
un individu a un tour de tête de 59 cm.il souhaite se confectionner un chapeau pointu pour la nouvelle année dont la forme et celle d’un cône de révolution.
1)Déterminer le rayon R du disque de base du chapeau .
L’individu souhaite que son chapeau ait une hauteur de 20 cm.
2)Déterminer SM .
3)Calculer l’angle du secteur circulaire du patron du chapeau .
Exercice 13 – Pyramide régulière et patron
Soit SABCD une pyramide régulière,
sa base est le carré ABCD de centre O
et le point A’ est le milieu de l’arrête [SA].SO=4 cm et AB=3 cm .
1)calculer la longueur SA .
2)faire un patron en vrai grandeur .
Exercice 14 – Position relative de droites et plans
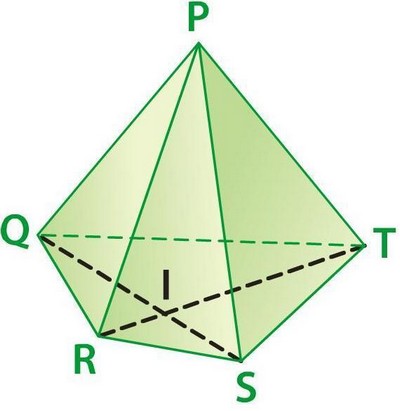
PQRST est une pyramide de sommet P et de base QRST
Les droites (QS) et (RT) se coupent en I.
Déterminer la position relative :
a) des droites (PI) et (QS)
b) des droites (PI) et (QT)
c) de la droite (RI) et du plan (QTP).
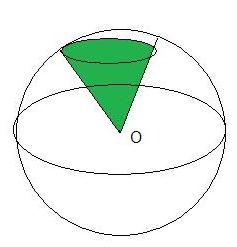
Exercice 15 – Cône dans une sphère
Un cône est dans un boule, le rayon de la boule est de 35 cm .
1. Calculer le volume de la boule .
2. Calculer le rayon du cône vert de hauteur 28 cm sachant que son sommet est en O et la génératrice du cône correspond au rayon de la boule .
Exercice 16 – Pyramide régulière
SABCD est une pyramide régulière à base carrée.
M est le milieu de [SA], N est le point de [SC] tel que .
1. Démontrer que les droites (MN) et (AC) sont sécantes.
2. Placer le point d’intersection de (MN) et (AC).
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «géométrie dans l'espace : exercices de maths en 2de corrigés en PDF.» au format PDF.
Réviser les leçons et les exercices avec nos Q.C.M :
.
.jpg)
Signaler une erreur
Aidez-nous à améliorer cette page en signalant une erreur
