Racine carrée : exercices de maths en 2de corrigés en PDF.

Les racines carrées à travers des exercices de maths en 2de corrigés afin d’assimiler toutes les propriétés sur la racine carrée et sa définition. Cette liste d‘énoncés est accompagnée de sa correction détaillée afin de s’exercer et de réviser en ligne ou de se préparer pour un contrôle. Vous pouvez également télécharger en PDF ou imprimer ces documents gratuits pour le niveau seconde.

Exercice 1 :

On pose $E=(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})-8\sqrt{5}(\sqrt{5}-1)$ .

Ecrire E sous forme $a+b\sqrt{5}$ .

( a et b étant des nombres relatifs) .

Exercice 2 :

Calculer D et E et donner les résultats sous la forme $a\sqrt{b}$ où a et b sont des nombres entiers avec b le plus petit possible.

$D=2\sqrt{12}-5\sqrt{27}+7\sqrt{75}$

$E=(\sqrt{2}+\sqrt{3})^2-5$

Exercice 3 :

On donne :

$A=\sqrt{12}+5\sqrt{75}-2\sqrt{27}$

$B=(5+\sqrt{3})^2-(2\sqrt{7})^2$

Ecrire A sous la forme $a\sqrt{3}$ et B sous la forme $b\sqrt{3}$ où a et b sont deux entiers relatifs .

Exercice 4 :

On pose :
$a=\sqrt{3}(1+\sqrt{6})\,;\, b=3-\sqrt{6}$

1. Calculer a², b² et a²+b² .

2. Montrer que a²+b² est un nombre entier .

3. Si a et b sont les longueurs des côtés de l’angle droit dans un triangle, quelle est la longueur de l’hypoténuse ?

Exercice 5 : une pièce rectangulaire.
Une pièce rectangulaire dont la longueur est le double de la largeur a une aire de 12,5 m².
Quelles sont ses dimensions?

Exercice 6 : racine carrée et pgcd.

1. Sans calculer leur PGCD, explique pourquoi les nombres 648 et 972 ne sont pas premiers entre eux.

2. a. Calculer PGCD ( 972 ; 648 ) en expliquant la méthode utilisée.

b. Démontrer que $\sqrt{648}+\sqrt{972}=18(\sqrt{3}+\sqrt{2})$ .

Exercice 7 : théorème de Pythagore.

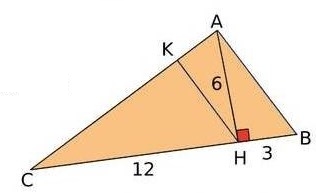
Considèrons la figure suivante, nous avons (KH) // (AB).

a. calculer les valeurs exactes de AC et AB.

b. Démontrer que le triangle ABC est rectangle en A.

c. Calculer la valeur exacte de KH.

Exercice 8

Calculer mentalement
$\sqrt{1}\,,\,\sqrt{0,04}\,,\,\sqrt{64}\,,\,\sqrt{10000}\,,\,-\sqrt{36}$ .

Exercice 9

Un élève a écrit :
$\sqrt{14}=7\,,\,\sqrt{9}=3\,$

A-t-il raison, (à justifier).

Exercice 10
Les nombres suivants sont-ils égaux à 3 ou à – 3 ?

${\sqrt{3}}^2\,,\,-\sqrt{9}\,,\,(-\sqrt{3})^2\,,\,-\sqrt{3^2}\,,\,\sqrt{(-3)^2}\,,\,-{\sqrt{3}}^2$ .

Exercice 11
a. Un carré a pour aire 13 cm².Combien mesure son côté ?

b. Un carré a pour côté $\sqrt{6}$ cm .

Quelle est son aire ?

Exercice 12
Simplifier :

$\sqrt{4}\times \sqrt{9}\,,\,\sqrt{0,01}\times \sqrt{225}\,,\,\sqrt{2^2\times 3^2\times 5^2}\,,\,\sqrt{\frac{4}{9}}\,,\,\sqrt{\frac{100}{81}}\,,\,\sqrt{\frac{30}{7}}\times \frac{\sqrt{21}}{\sqrt{40}}$ .

Exercice 13
a. Ecrire sous la forme $a\sqrt{b}$ les expressions suivantes :

$\sqrt{8}\,,\,\sqrt{54}\,,\,\sqrt{500}\,,\,\sqrt{0,07}\,,\,-\sqrt{125}$ .
b. Ecrire sous la forme $a\sqrt{7}$ ( a entier) :

$A=\,\sqrt{63}\,+\,2\sqrt{28}\,-\,\sqrt{700}$
$B=\,2\sqrt{28}\,-\,\sqrt{175}$

Exercice 14
Développer et réduire :
$A=\,(\sqrt{5}\,+\,\sqrt{7})^2$
$B=\,(\sqrt{7}\,-\,1)^2$
$C=\,(2\sqrt{2}-3)(2\sqrt{2}+3)$

Exercice 15

Montrer que E = 0.
$E=\,3\sqrt{54}-7\sqrt{6}-\sqrt{2}\times \sqrt{12}$

Exercice 16 : rectangle d’or.
Un rectangle est appelé rectangle d’or lorsque le quotient de sa longueur et de sa largeur est égale au nombre d’or.

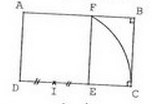
1. Construire un carré ADEF de côté 6 cm.

Placer le milieu I de [DE].

Tracer un arc de cercle de centre I, de rayon IF, comme sur la figure ci-dessous.

Terminer la construction comme ci-dessous.

2. démontrer que ABCD est un rectangle d’or.

Exercice 17 : simplifier des racines carrées.
On donne : $A=\sqrt{300}-4\sqrt{27}+6\sqrt{3}\\B=(5+\sqrt{3})^2\\C=(3\sqrt{2}+\sqrt{5})(3\sqrt{2}-\sqrt{5})$

a) Écrire A sous la forme $a\sqrt{3}$ , où a est un nombre entier.
b) Écrire B sous la forme $e+f\sqrt{3}$ , avec e et f entiers.

c) Montrer que C est un entier.

Exercice 18 : égalité complexe
Démontrer, sans utiliser la calculatrice, que :

$\frac{\sqrt{11}}{2\sqrt{3}-\sqrt{11}}=2\sqrt{33}+11$

Exercice 19 : développement et expression complexe
Développer et donner le résultat sous la forme

la plus simplifiée possible .

$K=2\sqrt{5}\times (3\sqrt{5}-1)-(3\sqrt{5}+2)\times (3\sqrt{5}-2)$

Exercice 20 : développer et réduire cette expression.
A = (27 -9)(27 )+9

Voir Exercices 11 à 20...

Exercice 21 :Points alignés.
Soient trois points O, U et I tels que : $UI=\sqrt{63}$ ; $OU=\sqrt{343}$ et $OI=\sqrt{700}$ .

Les points O, U et I sont-ils alignés ? Justifier.

Exercice 22 :Développer et réduire des racines.
Développer et réduire les expressions suivantes et donne le résultat sous la forme $a+b\sqrt{c}$ ,

où a et b sont des entiers relatifs et c un nombre entier positif.

$D=\sqrt{5}(\sqrt{5}-1)$

$E=\sqrt{2}(\sqrt{2}-5)-7\sqrt{2}$

Exercice 23 : géométrie.
Exprimer les aires de ces trois rectangles sous la forme $a+b\sqrt{5}$

(où et sont des nombres entiers ).

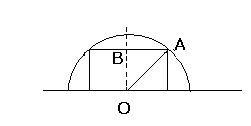
Exercice 24 : cloche à fromage et demi-cercle.
on dispose d’une cloche à fromage qui est une demi-sphère de rayon 9 cm. quelle est la hauteur maximum d’un fromage de la forme d’un cylindre de rayon 7 cm qui peut tenir sous cette cloche?
Expliquer.

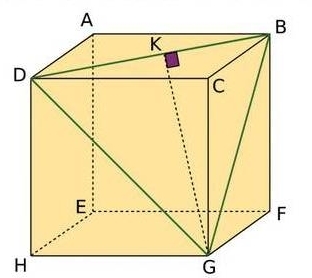
Exercice 25 : étude d’un cube.
ABCDEFGH est un cube de 4 cm d’arête.

a. Calculer la valeur exacte de GD et écrire le résultat sous la forme $a\sqrt{2}$ avec un nombre entier.

b. Quel est le périmètre du triangle BDG ?

Donner le résultat sous la forme $a\sqrt{2}$ avec un nombre entier.

c. Calculer la valeur exacte de GK.

d. Calculer l’aire du triangle BGD.

Donner la valeur exacte puis une valeur arrondie au centième.

Exercice 26 : spirale de Théodore de Cyrène.
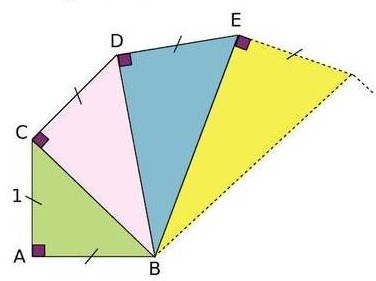
Observer la figure ci-dessous.

a. Sachant que le triangle ABC est un triangle rectangle isocèle en A, calculer la valeur exacte de BC.

b. En vous aidant de la figure ci-dessous et de la question a, calculer les valeurs exactes de DB et EB.

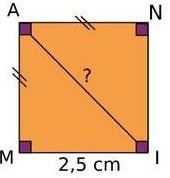
Exercice 27 : diagonales d’un carré.
On considère un carré ANIM.

a. Calculer la longueur exacte de la diagonale AI du carré MANI.

b. Si $AN=a\,(a>0)$ , que vaut la longueur AI ?

Carré

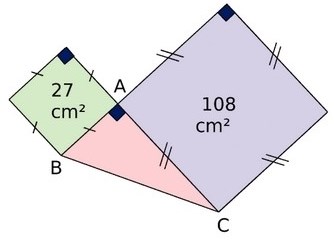
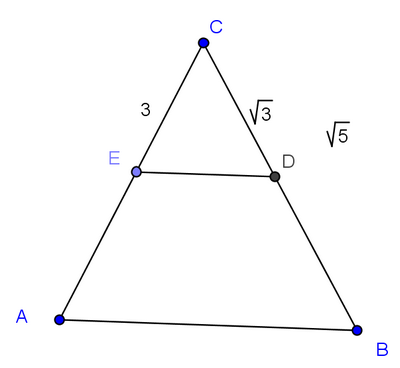
Exercice 28 : aires de triangles.
En utilisant les données de la figure, déterminer l’aire du triangle ABC.

Les proportions ne sont pas respectées.

Exercice 29 : développer un produit.
Développer et réduire : $(\sqrt{2}+3)(4-5\sqrt{2})$ .

Exercice 30 : développez en utilisant les identités remarquables.
$A=(1+\sqrt{2})^2$

$B=(2\sqrt{3}+4)^2$

$C=(\sqrt{5}-\sqrt{6})(\sqrt{5}+\sqrt{6})$

$D=(\sqrt{7}-\sqrt{2})^2$

Voir Exercices 21 à 30...

Exercice 31 : Simplification.
Simplifier les expressions suivantes et les mettre sous la forme $a\sqrt{b}$ , où a est un nombre entier relatif et b un nombre entier le plus petit possible.

$A=8\sqrt{7}-2\sqrt{28}+\sqrt{112}$

$B=2\sqrt{24}-3\sqrt{96}+9\sqrt{294}$

Exercice 32 : escargot de Pythagore.

En te servant du schéma ci-contre, trace un segment

de longueur $\sqrt{8}$ cm.

Explique ton raisonnement.

Exercice 33 : Fonctions numériques
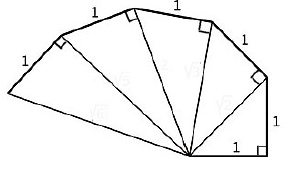
On considère la fonction h telle que

1. Calculer l’image de 1 par la fonction h.

2. Calculer l’image de $\sqrt{2}$ par la fonction h.

3. Calculer l’image de $2\sqrt{3}$ par la fonction h.

Exercice 34 : Volumes dans l’espace.
Un verre de la forme conique a une hauteur de 11 cm.

Quelle doit être la valeur exacte de la longueur de son diamètre, en cm, pour qu’il

contienne 25 cL ?

Exercice 35 : Diagonales d’un cerf volant.

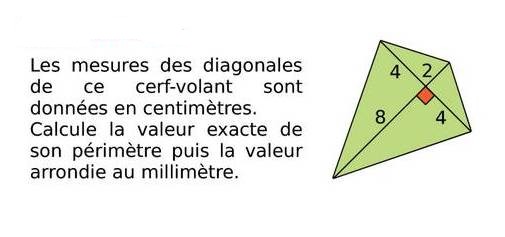
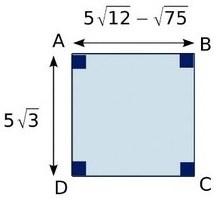
Exercice 36 : étude d’un carré.
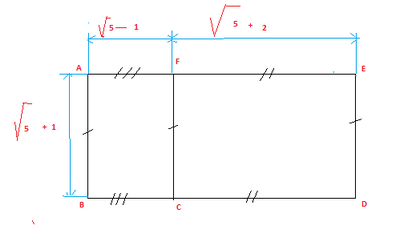
On considère la figure suivante. L’unité est le centimètre.

a. Ecrire $5\sqrt{12}-\sqrt{75}$ sous la forme $a\sqrt{b}$ , où et sont des entiers relatifs, étant le plus petit possible.

b. Quelle est le nature exacte de ABCD? Justifier votre réponse.

c. déterminer le périmètre de ABCD sous la forme la plus simple possible.

Donner, ensuite, l’arrondi au millimètre.

d. Déterminer la valeur exacte de l’aire de ABCD.

Exercice 37 : simplification de racines carrées.
Écrire sous la forme $a\sqrt{3}$ , a étant un entier naturel:

$A=\sqrt{27}+7\sqrt{75}-\sqrt{300}$ .

Ecrire sous la forme $p+m\sqrt{3}$ ou m et p sont des entiers relatifs :

$A=(3\sqrt{3}-2)(4-\sqrt{3})$

Exercice 38 : les racines carrées.
Mettre les nombres suivants sous la forme $a\sqrt{b}$

où et sont deux nombres entiers et le plus petit possible .

$t=\sqrt{96}\,\,\,;\,\,\,u=\sqrt{108}\,\,\,;\,\,\,v=\sqrt{162}$

Exercice 39 : calcul avec les racines.
Mettre les nombres suivants sous la forme $a\sqrt{5}$ .

$x=\sqrt{125}\,\,\,;\,\,\,y=\sqrt{500}\,\,\,;\,\,\,z=\sqrt{80}$

Exercice 40 : volume d’un prisme.
Calculer le volume d’un prisme droit de hauteur $\sqrt{20}$ cm et de base un triangle de dimensions: 1 cm; 3cm et $\sqrt{10}$ cm .

Ecrire le résultat sous la forme $a\sqrt{b}$ ( où et sont des nombres entiers ) .

Voir Exercices 31 à 40...

Exercice 41 : théorème de Thalès.
Les droites (AB) et (ED) sont parallèles .

$BC=\sqrt{5}$ ; $CD=\sqrt{3}$ et CE=3 .

Les longueurs sont en centimètres.

Calculer la longueur du segment [AC ] .

Exercice 42 : équations du type x²=a.
Résoudre les équations suivantes ( justifier vos réponses ) :

a) 3x² =75

b) x²= -36

c) 25x² =4

d) 49x² = -64 e) x²+9=0

f) 27x² = 12

Exercice 43 : fractions et produit de racines carrées.
Calculer le produit suivant et donner le résultat sous la forme la plus simplifiée possible .

$A=\frac{3\sqrt{5}-1}{\sqrt{5}+2}\times \frac{-\sqrt{15}}{\sqrt{5}-2}$

Exercice 44 : problème sur les racines carrées.
Soit a= $\sqrt{5}$ (1- $\sqrt{2}$ ) et b=5+ $\sqrt{2}$ .

a. Calculer a² et b².

b. En déduire les valeurs de a²+b² et $https://mathovore.fr/cgi-bin/mimetex.cgi?\sqrt{a²+b²}$ .

Exercice 45 : racine carrée et rectangle.
ABCD est un rectangle tel que :

$AB=(\sqrt{27}+\sqrt{3})\,\,cm$ et $BC=\sqrt{48}\,\,cm$ .

a) Démontrer que ABCD est un carré .

b) calculer son périmètre et son aire .

Exercice 46 :

Simplifier les expressions suivantes et les mettre sous la forme $a\sqrt{b}$ , où a est un nombre entier relatif et b un nombre entier le plus petit possible.

$A=8\sqrt{7}-2\sqrt{28}+\sqrt{112}$

$B=2\sqrt{24}-3\sqrt{96}+9\sqrt{294}$

Voir Exercices 41 à 46...

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «racine carrée : exercices de maths en 2de corrigés en PDF.» au format PDF.

Réviser les leçons et les exercices avec nos Q.C.M :

Q.C.M en 6ème Q.C.M en 5ème Q.C.M en 4ème Q.C.M en 3ème Q.C.M en 2de Q.C.M en 1ère Q.C.M en Terminale

D'autres fiches similaires :

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.