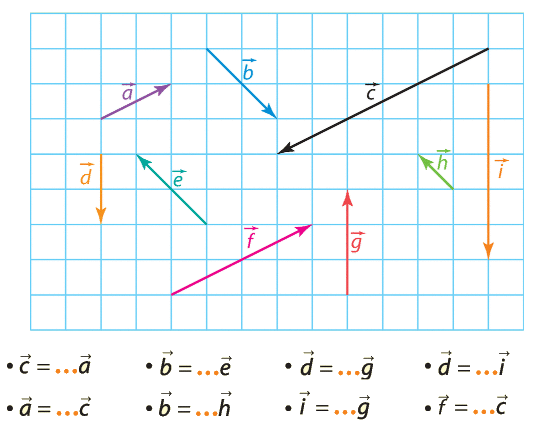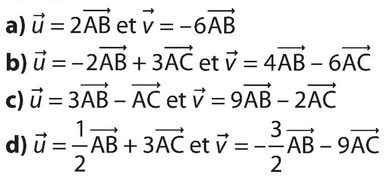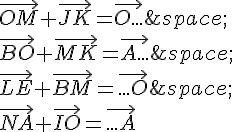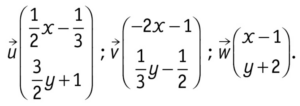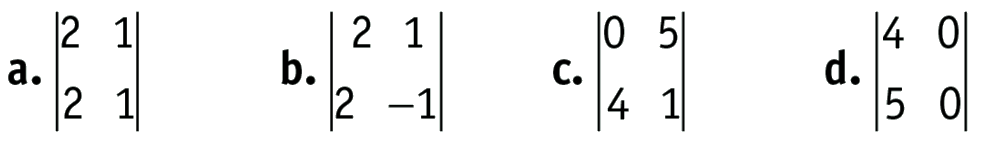Vecteurs et translation : exercices de maths en 2de corrigés en PDF.

Mis à jour le 29 mai 2025

Sommaire

✏️Exercices

2nde • Lycée

Vecteurs et translation

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Lycée

📱 Format : Gratuit

📄 PDF : Disponible

Les vecteurs et la translation à travers des exercices de maths en 2de corrigés. L’élève devra être capable de calculer des coordonnées et démontrer si des vecteurs sont colinéaires ou orthogonaux. Calculer une norme ou démontrer que des points du plan sont alignés. Savoir étudier une translation et construire l’image d’une figure à l’aide du matériel de géométrie.

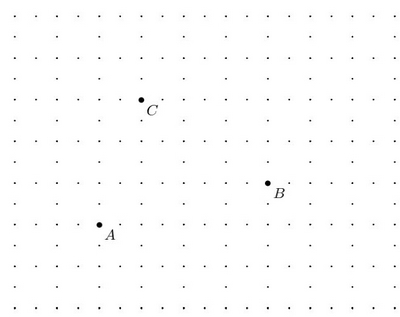
Exercice 1 – Les point sont-ils alignés

Les points P, Q et R sont-ils alignés ?

Exercice 2 – Points alignés et vecteurs

ABCD est un parallélogramme.
I est le milieu de [AB].
E est le point tel que $\vec{DE}=\frac{2}{3}\vec{DI}$

1. Effectuer la figure suivante.
2. Déterminer les coordonnées des points de la figure
dans le repère $(A;\vec{AB};\vec{AD})$ .
3. Les points A, E et C sont-ils alignés ?

Exercice 3 – Exprimer un vecteur en fonction de deux autres

A et B sont deux points distincts du plan .

On définit le point M par la relation vectorielle suivante :

$3\vec{MA}+\vec{MB}=\vec{0}$ .

1. Exprimer $\vec{AM}$ en fonction de $\vec{AB}$ .

2. Placer le point M .

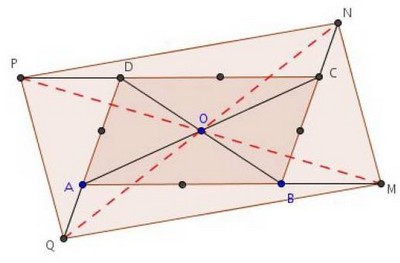
Exercice 4 – Etude d’un parallélogramme

ABCD est un parallélogramme de centre O. Les points M, N, P et Q sont tels que :

$\vec{AM}=\frac{3}{2}\vec{AB}\,;\,\vec{BN}=\frac{3}{2}\vec{BC}\,;\,\vec{CP}=\frac{3}{2}\vec{CD}\,;\,\vec{DQ}=\frac{3}{2}\vec{DA}$

a. Démontrer que $\vec{MB}=\vec{DP}$ .

b. Déduisez-en que O est le milieu de [MP] .

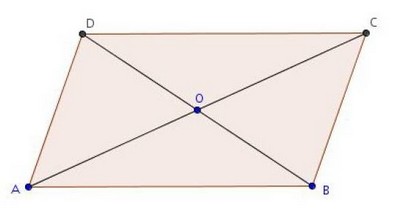
Exercice 5 – Parallélogramme
ABCD est un parallélogramme de centre O.
Donner l’ensemble des relations vectorielles possibles sur cette figure.

Exercice 6
(O,I,J) est un repère orthonormal avec OI=OJ=1 cm.

a. Placer les points A(-4;6), B(-2;-3),C(2;0),D(0;3), E(2;3).

b. Quelles sont les coordonnées des points A et B dans le repere (O;C,D)dans le repère (O;D,C)?

c. Quelles sont les coordonnées du point O dans le repère (E;C,D)?

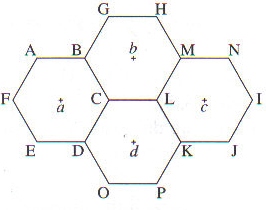
Exercice 7

La figure ci-dessous représente des hexagones réguliers de centres a,b,c,d.

1. Déterminer les images de chacun des points C,E,A,M par la translation de vecteur :

a. $\vec{AB}$

b. $\vec{BC}$

c. $\vec{AC}$

2. Démontrer que C est le milieu de [AK].

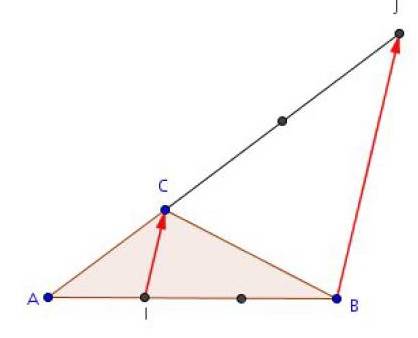
Exercice 8

Démontrer que pour tous points A, B, C, D.

$\fbox{\vec{AD}+\vec{BC}=\vec{AC}+\vec{BD}}$ .

Exercice 9

Dans un répère, on considère les points A(-5;3), B(2;-1), C(0;4).

a. Placer les points A,B,C.

b. Calculer les coordonnées des vecteurs $\vec{AB},\vec{AC},\vec{BC}.$ .

c. En déduire les coordonnées du point M tel que $\vec{AM}=\vec{u}.$

d. Vérifier que B est le milieu de [AM] .

e. Calculer la distance AB .

Exercice 10

ABC est un triangle.

D,E,F sont les points tels que :

$\vec{CD}=-\vec{CB}\,;\,\vec{AE}=\frac{3}{2}\vec{AC}\,;\,\vec{BF}=-2\vec{BA} .$

Démontrer que les points D, E, F sont alignes .

Indication : utiliser la relation de Chasles .

Exercice 11 – Droite d’EULER d’un triangle
ABC est un triangle scalène*. A’, B’, C’ sont les milieux respectifs des côtés [BC], [AC] et [AB].
O est le centre de son cercle circonscrit.

1. On note P le point défini par $\vec{OP}= \vec{OA}+\vec{OB}+\vec{OC}$
a. Faire une construction à la main ou avec le logiciel de géométrie « GEOGEBRA ».
b. Montrer que: $\vec{AP}= 2. \vec{OA'}$

c. Démontrer que (AP) est perpendiculaire à (BC).
d. Démontrer de même que (BP) est perpendiculaire à (AC)
e. Quelle position particulière occupe le point P ? (Dans la suite de l’exercice le point P sera noté H)

2. On note G le centre de gravité du triangle ABC, c’est à dire le point d’intersection des médianes.
On rappelle que si G est le centre de gravité du triangle ABC alors :

$\vec{GA}+\vec{GB}+\vec{GC}= \vec{0}$
Montrer que :
$\vec{OH} = 3. \vec{OG}$

Que déduit-on alors de la position des points O, H et G ?

Notes :

1- Scalène : un triangle est dit «scalène» lorsque ses trois côtés ont des mesures différentes.
Un triangle scalène n’est ni rectangle, ni isocèle, ni équilatéral.

2- La droite qui passe par les trois points O , H , G est appelée : « Droite d’EULER du triangle ».

Exercice 12 – Des perpendiculaires dans un triangle

On considère un triangle isocèle de base [BC] et de sommet A.

On désigne par O le centre du cercle circonscrit à ce triangle.

On désigne par M le milieu de [AB] et par G le centre de gravité du triangle AMC.

Montrer que les droites (MC) et (OG) sont perpendiculaires.

Exercice 13 – Orthogonalité dans un triangle

On considère un triangle ABC et son cercle circonscrit de centre O.

On désigne par H l’orthocentre du triangle ABC et par M le milieu de [BC].

La droite (MH) coupe, l’arc $\overset{\frown}{AB}$ qui ne contient pas C, en I.

Montrez que les droites (MH) et (AI) sont perpendiculaires.

Exercice 14 – Déterminer les coordonnées d’un point M

Dans un repère $(O;\vec{i};\vec{j})$ , on donne K ( – 3 ; 5) et L(4 ; 2).
Déterminer l’abscisse du point M d’ordonnée – 2 tel que K, L et M soient alignés.

Exercice 15 – Etude de droites dans un repère

Dans un repère $(O;\vec{i},\vec{j})$ , on donne A(2 ;- 3) B(0 ; – 3) C( – 3 ; 0).

1. Déterminer par le calcul les coordonnées du point E tel que $\vec{CE}=\frac{1}{2}\vec{AB}$ .

2. Que peut-on dire des droites (CE) et (AB) ? Justifier.

3. Donner les équations de (CE) et (AB).

Exercice 16 – Points alignés dans un repère

Dans un repère $(O;\vec{i},\vec{j})$ , on donne :

E(3 ; – 1) F(7 ; – 7) G(5 ; – 4).

Déterminer si les trois points E, F et G sont alignés.

Exercice 17 – Coordonnées et vecteurs colinéaires

1. Les vecteurs $\vec{u}(1+\sqrt{3};4)$ et $\vec{v}(\frac{1}{2};\sqrt{3}-1)$ sont-ils colinéaires ?

2. Déterminer tel que les vecteurs $\vec{u}(2;m)$ et $\vec{v}(5;-1)$ soient colinéaires.

Exercice 18 – Quatre points quelconques du plan

Soient A, B, C et D, quatre points quelconques du plan.

Montrer que :

$3\vec{DA}-\vec{DB}-2\vec{DC}=3\vec{BA}-2\vec{BC}$

Exercice 19 – Démontrer que des points sont confondus

Démontrer que les points B et D sont confondus sachant que :

$\vec{BA}+\vec{CB}+\vec{DC}=\vec{CA}+\vec{DB}-\vec{CD}$

Exercice 20 – Problème sur les vecteurs
A et B sont deux points distincts.

On cherche à construire le point M tel que :

$3\vec{MA}+4\vec{MB}=\vec{0}$

1. Les vecteurs $\vec{MA}$ et $\vec{MB}$ sont-ils colinéaires ?ont-ils le même sens?ont-ils la même norme?

2. En utilisant la relation de Chasles, montrer que l’on a l’égalité :

$7\vec{MA}+4\vec{AB}=\vec{0}$

3. En déduire $\vec{AM}$ en fonction de $\vec{AB}$ .

Construire le point M.

Exercice 21 – Colinéarité de deux vecteurs

Les vecteurs $\vec{u}(\sqrt{2};1-\sqrt{3})$ et $\vec{v}(1+\sqrt{3};-\sqrt{2})$ sont-ils colinéaires ?

Exercice 22 – Relation de Chasles

On considère un triangle ABC et les points I et J tels que :

$\vec{AI}=\frac{1}{3}\vec{AB}$

$\vec{AJ}=3\vec{AC}$

1. Montrer à l’aide de la relation de Chasles que $\vec{BJ}=3\vec{IC}$ .

2. Que peut-on en déduire pour les droites (BJ) et (IC) ?

Exercice 23 – Vecteurs colinéaires

Dans chacun des cas suivants, montrer que les vecteurs $\vec{AB}$ et $\vec{CD}$ sont colinéaires.

1. $\vec{AC}+\vec{DC}=\vec{BD}$ .

2. $2\vec{CB}-9\vec{CA}-7\vec{AD}=\vec{0}$

Exercice 24 – Démontrer que deux points sont confondus

Démontrer que les points A et D sont confondus sachant que :

$\vec{AC}+\vec{AD}-\vec{BC}=\vec{AB}$ .

Exercice 25 – Placer des points à partir d’égalités vectorielles

1. Placer le point E tel que $\vec{BE}=\vec{AC}$ .

2. Placer le point F tel que $\vec{BF}=-\vec{AC}$ .

3. Placer le point G tel que $\vec{BG}=\vec{AC}+\vec{BA}$ .

Exercice 26

(O,I,J) est un repère orthonormal avec OI=OJ=1 cm.

a. Placer les points A(-4;6), B(-2;-3),C(2;0),D(0;3), E(2;3).

b. Quelles sont les coordonnées des points A et B dans le repère (O;C,D)dans le repère (O;D,C)?

c. Quelles sont les coordonnées du point O dans le repère (E;C,D)?

Exercice 27

Démontrer que pour tous points A, B, C, D.

$\fbox{\vec{AD}+\vec{BC}=\vec{AC}+\vec{BD}}$ .

Exercice 28

Dans un repère, on considère les points A(-5;3), B(2;-1), C(0;4).
a. Placer les points A,B,C.
b. Calculer les coordonnées des vecteurs $\vec{AB},\vec{AC},\vec{BC}.$ .
c. En déduire les coordonnées du point M tel que $\vec{AM}=\vec{u}.$

d. Vérifier que B est le milieu de [AM] .

e. Calculer la distance AB .

Exercice 29

ABC est un triangle.
D,E,F sont les points tels que :

$\vec{CD}=-\vec{CB}\,;\,\vec{AE}=\frac{3}{2}\vec{AC}\,;\,\vec{BF}=-2\vec{BA} .$

Démontrer que les points D, E, F sont alignés .

Indication : utiliser la relation de Chasles .

Exercice 30 – Coordonnées de points et longueurs

Dans le plan muni d’un repère orthonormé, on note E l’ensemble des points dont les coordonnées (x;y) vérifient la relation :

$\frac{x^2}{25}+\frac{y^2}{9}=1$ .

On considère également les points F(4;0) et F'(-4;0).
1. Calculer les coordonnées des points d’intersection de E avec les axes du repères.
2. A l’aide du logiciel Geogebra, visualiser l’ensemble E et faire une conjecture sur la somme des distances MF + MF’ lorsque M est un point de E.
3. Soit M(x;y) un point de E.
a) Exprimer en fonction de et en déduire que $x^2\leq\, 25$ .

b) Montrer que $MF^2=(\frac{4}{5}x-5)^2$ .

c) Sachant que $x\leq\, 5$ , montrer que $\frac{4}{5}x-5\leq\, 0$

puis en déduire que $MF=5-\frac{4}{5}x$ .

d) Valider la conjecture .

Exercice 31 – Vecteurs et parallélogramme

Soit ABCD est un parallélogramme .

1) Placer les points M et N définis par les égalités suivantes:

$\vec{AM}=\vec{AD}+\frac{2}{5}\times \vec{DB}$

$\vec{CN}=-\vec{CB}-\frac{1}{3}\times \vec{BA}$

2) Montrer en utilisant la relation de chasles que $\vec{DN}=-\vec{CB}-\frac{2}{3}\times \vec{BA}$ .

3) Exprimer le vecteur $\vec{DN}$ en fonction des vecteurs $\vec{AD}$ et $\vec{DB}$ .

Exercice 32 – Coordonnées dans un repère orthonormé

Dans un repère orthonormal $(O,\vec{i},\vec{j})$ , on donne les points :
A(5 ; 4), B(– 1 ; 6) et C(– 3 ; 1)

1° a) Placer le point D tel que ABCD soit un parallélogramme.
Déterminer les coordonnées de D.

b) Calculer les coordonnées du point I centre du parallélogramme ABCD.

c) Le point F est le symétrique du point C par rapport au point E(– 2 ; – 1).
Calculer les coordonnées de F.

d) Calculer les coordonnées des vecteurs $\vec{EI}$ et $\vec{FA}$ .

Que remarque-t-on ? Pouvait-on prévoir ce résultat ?

2° Soit le point M défini par : $\vec{AM}+3\vec{DM}=\vec{0}$ .

a) Calculer les coordonnées du point M.

b) Les points M, I et D sont-ils alignés ?

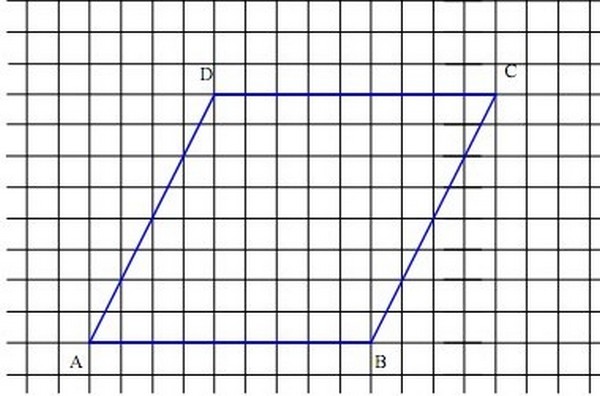
Exercice 33 – Vecteurs et parallèles
Soit ABCD un parallélogramme et soit les points M,N et P définis par :

$\vec{AM}=\frac{3}{8}\vec{AD}\,\,;\,\vec{BN}=\frac{3}{4}\vec{BC}\,\,;\,\vec{CP}=\frac{2}{3}\vec{CD}$

1. Construire les points M, N et P sur la figure ci-dessous.
2. On veut démontrer que les droites (BM) et (PN) sont parallèles.

On propose deux méthode au choix :

Méthode A :

a) Exprimer les vecteurs $\vec{BM}$ et $\vec{PN}$

en fonction de $\vec{AB}$ et $\vec{AD}$ .

b) Que peut-on dire des vecteurs $\vec{BM}$ et $\vec{PN}$ .

c) Conclure

Méthode B :

On se place dans le repère $(A,\vec{AB},\vec{AD})$

a) Donner (sans justification) les coordonnées des
points A, B, C et D.

b) Calculer les coordonnées des points M, N et P.

c) Conclure

Exercice 34 :

Soit ABCD un trapèze convexe tel que : (AB)//(DC), AB = 5 et DC = 7.

1) a) A partir de ces hypothèses, montrer que $\vec{DC}=\frac{7}{5}\vec{AB}$

b) Exprimer $\vec{AC}$ en fonction de $\vec{AB}$ et $\vec{AD}$ .

2) On considère le point E tel que 5 $\vec{EC}$ = 2 $\vec{DE}$

a) Déterminer $\vec{DE}$ en fonction de $\vec{DC}$ , puis placer E.

b) Montrer que les segments [AE] et [BD] ont même milieu.

3) A chaque réel x , on fait correspondre le point M tel que $\vec{AM}$ = x $\vec{AB}$ + $\vec{AD}$ .

a) Pour quelle valeur de x le point M est-il le symétrique de C par rapport à D ?

b) Exprimer $\vec{DM}$ en fonction de $\vec{AB}$ . Sur quelle ligne se déplace le point M lorsque x varie ?

Exercice 35 :

Soit ABC un triangle et x un réel.

A chaque valeur de x on associe les points E et F tels que : $\vec{AE}=\frac{1}{3}\vec{AB}\,+x\vec{AC}$ et $\vec{AF}=x\vec{AB}\,+\frac{1}{3}\vec{AC}$

1) Construire E et F pour $x=-\frac{1}{2}$ .

2) Montrer que, pour tout x de $\mathbb{R}$ , $\vec{EF}$ est colinéaire à $\vec{BC}$ .

3) Pour quelles valeurs de x a-t-on :

a) E = F ?

b) BCFE est un parallélogramme ?

Exercice 36 :

Soit ABCD un quadrilatère, on défini les points M et N par : $\vec{AM}=a\vec{AB}$ et $\vec{DN}=a\vec{DC}$ ( a étant un réel)

1) Montrer que pour tout réel a , on a : $\vec{MN}=a\vec{BC}\,+(1-a)\vec{AD}$

2) Que dire de MBCN si ABCD est un parallélogramme ?

Exercice 37 :

Soit un réel a et un triangle RST. Soit aussi les points M, N et U définis par
$\vec{RM}=\frac{1}{4}\vec{RS}\,+(a+\frac{5}{2})\vec{RT}$ ; $\vec{RN}=(a+2)\vec{RS}\,+\frac{3}{4}\vec{RT}$ ; $\vec{RU}=\,\frac{3}{4}\vec{RS}\,-(a+\,\frac{3}{2})\vec{RT}$

1) Placer les points M, N et U lorsque a = 0.

2) Démontrer que pour tout réel a , les vecteurs $\vec{MN}$ et $\vec{ST}$ sont colinéaires. Que peut-on en déduire ?

3) Démontrer que pour tout réel a , SMTU est un parallélogramme

Exercice 38 :

Soit ABC un triangle.

1) On donne G tel que $\vec{GA}\,+2\vec{GB}\,+3\vec{GC}\,=\vec{0}$ .
Déterminer $\vec{CG}$ en fonction de $\vec{CA}$ et $\vec{CB}$ puis construire G.

2) Soit H tel que $\vec{AH}\,=\frac{2}{3}\vec{AB}$ , montrer que G est le milieu de [HC]

3) Montrer que pour tout point M, $\vec{MA}+2\vec{MB}\,+3\vec{MC}\,=6\vec{MG}$ .

4) Déterminer et construire l’ensemble des points M du plan tels que :

a) $\,\|\,\vec{MA}+2\vec{MB}\,+3\vec{MC}\,\,\|=6AB$ .

b) $\vec{MA}+2\vec{MB}\,+3\vec{MC}$ est colinéaire à $\vec{BC}$ .

Exercice 39 :

Recopier et compléter les égalités suivantes avec le nombre réel manquant.

Exercice 40 :

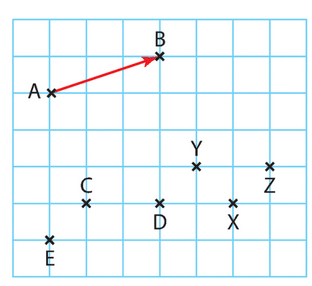
1.A partir de la figure, citer un vecteur :

a) opposé à $\vec{CD}$ .

b) de même direction et de même sens que $\vec{AC}$ .

c) de même direction que $\vec{BC}$ mais de sens contraire.

d) égal au vecteur $\vec{BA}$ .

Exercice 41 :

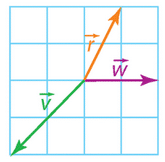
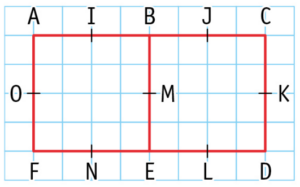
A partir de la figure :

Donner les images des points C, D, E par la translation de vecteur $\vec{AB}$ .
Citer trois vecteurs égaux au vecteur $\vec{AB}$ .
Citer les trois parallélogrammes définis par les trois égalités vectorielles du 2.

Exercice 42 :

1.Reproduire la figure ci-dessous.

2.Construire un représentant de chacun des vecteurs suivants.

$a)-\vec{r}$ $b)\vec{w}+\vec{r}$ $c)\vec{r}+\vec{v}$ $d)\vec{w}-\vec{r}$

Exercice 43 :

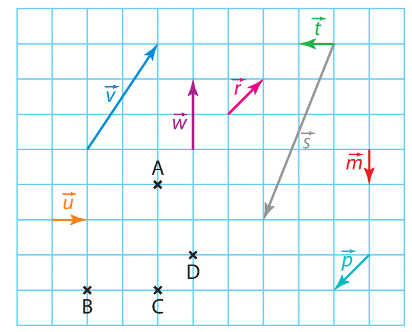
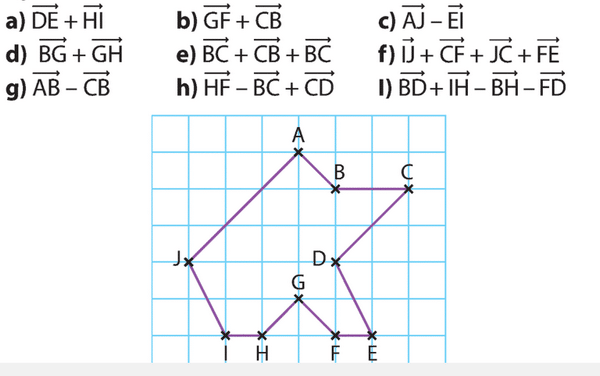
En utilisant les points de la figure, donner un vecteur égal à :

Exercice 44 :

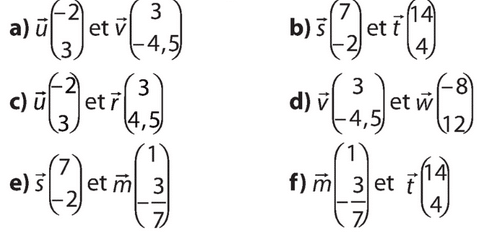
Calculer les déterminants des vecteurs suivants.
Dire s’ils sont colinéaires.
S’ils sot colinéaires, trouver un coefficient de colinéarité.

Exercice 45 :

Soit trois points A, B et C distincts non alignés.

Les vecteurs $\vec{u}$ et $\vec{v}$ sont-ils colinéaires dans les cas suivants ?

Exercice 46 :

Compléter :

$\vec{OM}+\vec{JK}=\vec{O...}\,\\\vec{BO}+\vec{MK}=\vec{A...}\,\\\vec{LE}+\vec{BM}=\vec{...O}\,\\\vec{NA}+\vec{IO}=\vec{...A}$

Exercice 47 :

Soient les vecteurs :

2 Déterminer les valeurs des réels x et y pour que :

a. $\vec{u}-\vec{v}\,=\,\vec{w}$

b. $3\vec{u}=-\vec{v}+\frac{1}{2}\vec{w}$

c. $-4\vec{u}+3\vec{v}-\frac{2}{3}\vec{w}=\vec{0}$

Exercice 48 :

Calculer les déterminants suivants :

Exercice 49 :
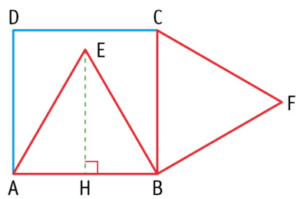
Soit un carré ABCD de côté de longueur 1, ABE et CFD sont des triangles équilatéraux.

Soit H le pied de la hauteur issue de E du triangle ABE.
1.Calculer la longueur EH.
2.Dans toute la suite on considère de repère $(A,\,\vec{AB},\,\vec{AD})$

a. Montrer que le repère $(A,\,\vec{AB},\,\vec{AD})$ est orthonormé.
b. Déterminer les coordonnées de tous les points de la figure dans le repère $(A,\,\vec{AB},\,\vec{AD})$ .
c. En déduire que les points D, E et F sont alignés.

5/5 - (21701 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «vecteurs et translation : exercices de maths en 2de corrigés en PDF.» au format PDF.