Probabilités : exercices de maths en 2de corrigés en PDF.
Mis à jour le 4 avril 2025
Exercice 1 :
1.
a. Effectuer 50 lancers de deux pièces.
Pour chaque lancer, noter l’évènement qui est réalisé :
A: « Obtenir deux fois Pile »;
B:Obtenir deux fois face;
C: Obtenir une fois Pile et une fois Face ».
b. Calculer la fréquence de chacun des évènements A,B et C.
2. Effectuer une nouvelle série de 50 lancers et calculer également les fréquences de A, B et C.
Exercice 2 :
Proposer une façon de simuler le tirage au sort de 20 élèves parmi 832 élèves d’un lycée.
Exercice 3 :
Dans certains pays, on recommande aux couples, souhaitant fonder une famille, d’avoir des enfants jusqu’à ce que les deux sexes soient représentés.
1. Donner une façon de simuler la composition d’une famille obéissant à cette politique.
2.
a. Réaliser 100 simulations et noter, à chaque fois, le nombre d’enfants de la famille.
b. Calculer, pour l’échantillon obtenu, le nombre moyen d’enfants par famille.
Exercice 4 :
On lance un dé équilibré et on s’intéresse au nombre de lancers nécessaires pour obtenir les six chiffres .
Par exemple, la réalisation : 2 3 5 3 4 2 6 3 5 6 2 4 4 1 a nécessité 14 lancers pour obtenir les six chiffres.
a. Réaliser des simulations de cette expérience pour obtenir les six chiffres .
b. Estimer le nombre moyen de lancers nécessaires pour obtenir les six chiffres .
Exercice 5 :
Voici les 100 premiers chiffres de l’écriture décimale de Pi :
3,1415 92653 58979 32384 62643
38327 95028 84197 16939 93751
05820 97494 45923 07816 40628
62089 98628 03482 53421 17067
1- On prend au hasard l’un des 30 premiers chiffres.
Déterminer la probabilités que ce soit :
a-0 b-1 c-2 d-3
2- Reprendre la question 1 avec :
a- les 50 premiers chiffres
b- les 100 premiers chiffres.
Exercice 6 :
Dans une loterie, une roue est divisée en secteurs tous identiques :
neuf de ces secteurs permettent de gagner 5€, six permettent de gagner 10€, trois permettent de gagner 50€, deux permettent de gagner 100€ et quatre ne font rien gagner.
1) Quelle est la probabilité de ne rien gagner ? Justifie ta réponse.
2) Quelle est la probabilité de gagner au moins 50€ ? Justifie ta réponse.
Exercice 7 :
On lance un dé cubique équilibré dont les faces sont numérotées de 1 à 6 et on considère le numéro de la face supérieure.
a. Quel est l’univers associé à cette expérience aléatoire ?
b. Pourquoi est-on en situation d’équiprobabilité ?
c. Quelle est la probabilité d’obtenir chacune des faces ?
d. La probabilité d’obtenir un nombre pair est-elle égale à celle d’obtenir un nombre impair.
Exercice 8 :
On lance un dé équilibré à 20 faces numérotés de 1 à 20 et on considère le numéro de la face supérieure.
1.Quel est l’univers associé à cette expérience aléatoire ?
2.Pourquoi est-on en situation d’équiprobabilité ?
3.Calculer la probabilité d’obtenir :
a. un nombre impair ?
b. un nombre multiple de 3 ?
c. un nombre divisible par 5 ?
d. un nombre multiple de 15 ?
4. Quelle est la probabilité d’obtenir un nombre multiple de 3 ou de 5 ?
Exercice 9 :
On dispose de trois pièces de monnaie équilibrée : une Française, une Allemande et une Italienne.
On choisit une pièce au hasard et on la lance. On observe la face obtenue.
On note F l’événement « la pièce est française », A l’événement « la pièce est allemande » et P
l’événement « obtenir Pile lors du lancer ».
a. Réaliser un arbre permettant de regrouper toutes les issues possibles.
b. Déterminer la probabilité d’obtenir la pièce française.
c. Calculer la probabilité d’obtenir Pile sur la pièce allemande.
Écrire cette probabilité à l’aide des événements A et P.
d. Traduire par une phrase l’événement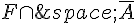 
et calculer sa probabilité.
Exercice 10 :
À la cafeteria, des lycéens souhaitent jouer au jeu « Loup-Garou ».
Voici la composition du jeu de cartes :
13 villageois, 1 chasseur, 4 Loups-Garous,
1 cupidon, 1 sorcière, 1 voyante
1 petite fille, 1 capitaine, 1 voleur.
Un premier joueur tire une carte au hasard.
Quelle est la probabilité :
a. qu’il obtienne une carte Loup-Garou ?
b. qu’il obtienne une carte Villageois ?
c. qu’il n’obtienne ni une carte Loup-Garou, ni une carte Villageois ?
Exercice 11 :
On fait tourner une roue divisée en douze secteurs égaux, identique à la roue ci-contre. On lance
la roue et on observe la couleur repérée.
Déterminer la probabilité :
a. d’obtenir le secteur orange.
b. d’obtenir un secteur de couleur bleu.
c. de ne pas obtenir un secteur de couleur bleu.
Exercice 12 :
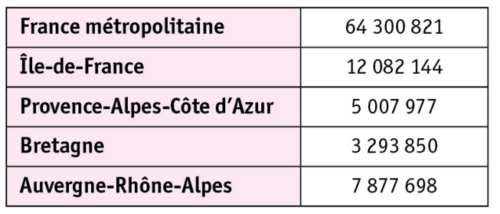
Voici la répartition de la population dans certaines régions françaises en 2015 :
On choisit au hasard une personne qui vivait en France en 2015.
Arrondir les probabilités à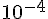
Déterminer la probabilité qu’en 2015, elle ait habité :
a. en Auvergne-Rhône-Alpes ;
b. en Île-de-France ;
c. en Provence-Alpes-Côte d’Azur ou en Bretagne.
Exercice 13 :
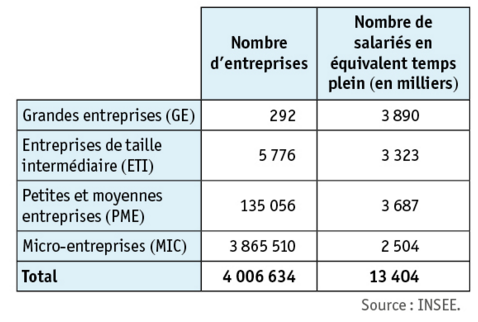
Le tableau ci-après donne les caractéristiques des entreprises françaises par catégorie en 2016 (y compris les activités financières et assurances).
Arrondir les probabilités demandées à .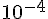
1.On choisit au hasard une de ces entreprises.
Déterminer la probabilité que l’entreprise :
a. soit de taille intermédiaire ;
b. ne soit pas une grande entreprise.
2.On choisit au hasard un salarié d’une de ces entreprises.
Déterminer la probabilité qu’il travaille :
a. dans une grande entreprise ;
b. dans une PME ou dans une MIC.
Exercice 14 :
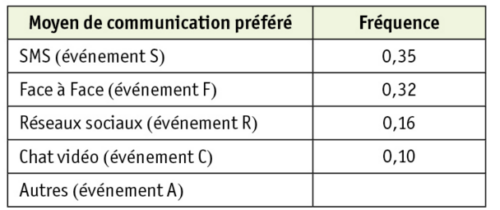
Un sondage auprès de lycéens a été réalisé sur leur moyen de communication préféré.
Les résultats sont donnés dans le tableau ci-dessous :
1.Déterminer la fréquence des lycéens qui utilisent un autre moyen de communication.
2.On choisit un de ces lycéens au hasard.
a. Déterminer la probabilité .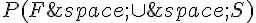
b. Traduire par une phrase l’événement 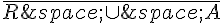puis calculer sa probabilité.
c. Traduire par une phrase l’événement 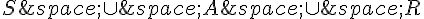puis calculer sa probabilité.
Exercice 15 :
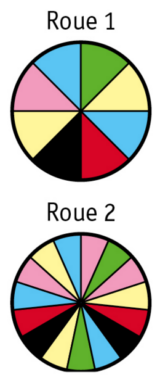
Sacha a le choix entre les deux roues de loterie équilibrées ci-dessous (les secteurs sont de même dimension) :
Il remporte un gros lot s’il obtient un secteur de couleur rouge.
Quelle roue doit-il choisir pour avoir le plus de chance de remporter le gros lot ?
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «probabilités : exercices de maths en 2de corrigés en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.
