Généralités sur les fonctions : cours de maths en 2de en PDF.

Sommaire de cette fiche

1 I. Opérations algébriques sur les fonctions :
2 II. Sens de variation:
3 Vous avez assimilé ce cours sur les généralités sur les fonctions en 2de?

Les généralités sur les fonctions numériques dans un cours de maths en 2de où nous étudierons les opérations sur les fonctions ainsi que les égalités. dans cette leçon en seconde, nous aborderons le sens de variation d’une somme, produit et composée de fonctions numériques.

I. Opérations algébriques sur les fonctions :

1. Egalité :

Définition :

Dire que deux fonctions f et g sont égales, ce que l’on note alors f = g, signifie qu’elles ont le même ensemble de définition D et que, pour tout x de D, f(x) = g(x).

2. Opérations :

Propriété :

Soient f et g deux fonctions définies respectivement sur Df et Dg.
Opérations :

Opération	Notation	Definition	Definie pour :
Somme	f+g	$\,D_f\cap\,D_g$
Différence	f-g	x f(x)-g(x)	$\,D_f\cap\,D_g$
Produit	fg	x f(x)g(x)	$\,D_f\cap\,D_g$
quotient	$\frac{f}{g}$	x $\,\frac{f(x)}{g(x)}$	$\,D_f\cap\,D_g-\{x\in\,D_g\,,\,g(x)\neq\,0}$

3. Composition de fonctions :

Définition :

Etant donné deux fonction f et g, la fonction gof (lire « g rond f ») est la fonction definie par

$\,\fbox{gof(x)=g[f(x)]}$

L’ensemble de définition de gof est constitué de tous les nombres x tels que x soit dans Df et f(x) soit dans Dg.

Exemple :

f est la fonction définie sur R par f(x)=x-2 et g est la fonction carrée.
Dans g(x), on remplace x par f(x).
Alors g(f(x))= (x-2)²
Donc gof est la fonction x 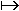(x-2)² définie sur R.

II. Sens de variation:

1. Sens de variation d’une somme de fonction :

Théorème :

La somme de deux fonctions strictement croissantes sur un intervalle I est une fonction strictement croissante sur I.
La somme de deux fonctions strictement décroissantes sur un intervalle I est une fonction strictement décroissante sur I.

2. Sens de variation de ku :

Définition :

Soit u une fonction définie sur un intervalle I et k un nombre réel.
ku est la fonction x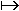 ku(x).

Exemple :

si u(x)=x²+3, la fonction 5u (ici k=5) est x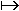 5(x²+3) ainsi (5u)(x)=5x²+15.

Théorème :

Si k>0, u et ku ont le même sens de variation sur I.
Si k<0, u et ku varient en sens contraires sur I.

3. Sens de variation d’une composée de fonctions :

Théorème :

Soient f et g deux fonctions strictement monotones, I est un intervalle inclus dans Df,
J un intervalle inclus dans Dg tel que pour tout x dans I, f(x) soit dans J.

Lorsque f et g ont même sens de variation, alors gof est strictement croissante sur I.
Lorsque f et g ont des sens de variation différents, alors gof est strictement décroissante sur I.

3.4/5 - (23 votes)

Télécharger et imprimer ce document en PDF gratuitement

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «généralités sur les fonctions numériques : cours de maths en 2de» au format PDF.

Télécharger nos applications gratuites avec tous les cours,exercices corrigés.

D'autres fiches similaires à généralités sur les fonctions numériques : cours de maths en 2de.

Mathovore vous permet de réviser en ligne et de progresser en mathématiques tout au long de l'année scolaire.
De nombreuses ressources destinées aux élèves désireux de combler leurs lacunes en maths et d'envisager une progression constante. Tous les cours en primaire, au collège, au lycée mais également, en maths supérieures et spéciales ainsi qu'en licence sont disponibles sur notre sites web de mathématiques.
Des documents similaires à généralités sur les fonctions numériques : cours de maths en 2de à télécharger ou à imprimer gratuitement en PDF avec tous les cours de maths du collège au lycée et post bac rédigés par des enseignants de l'éducation nationale.
Vérifiez si vous avez acquis le contenu des différentes leçons (définition, propriétés, téhorèmpe) en vous exerçant sur des milliers d'exercices de maths disponibles sur Mathovore et chacun de ces exercices dispose de son corrigé.
En complément des cours et exercices sur le thème généralités sur les fonctions numériques : cours de maths en 2de, les élèves de troisième pourront réviser le brevet de maths en ligne ainsi que pour les élèves de terminale pourront s'exercer sur les sujets corrigé du baccalauréat de maths en ligne.

Calcul littéral : correction des exercices en troisième
63
Développer avec les identités remarquables, exercices corrigés de mathématiques en troisième (3ème) sur les identités remarquables. Exercice: Développer en utilisant les identités remarquable : Exercice : On considère les expressions E = x² − 5x + 5 et F = (2x − 7)(x − 2) − (x − 3)² .…
Les équations et inéquations : correction des exercices en troisième
61
Résoudre des équations du premier degré à une inconnue.Exercices corrigés de mathématiques en troisième (3ème). Exercice : Exercice : Déterminer trois nombres entier positifs consécutifs dont la somme des carrés est égale à 1 325. Pour la facilité des calculs on choisira les nombres consécutifs suivants : n-1…
Problèmes de maths et calculs à résoudre à imprimer en PDF.
59
La série des problèmes ouverts de maths afin de réfléchir sur des exercices complexes avec un travail individuel ou en groupe.Ces exercices développe l'esprit d'initiative et le raisonnement scientifique pour les élèves du collège et du lycée. Une série de problèmes ouverts afin de développer la prise d'initiative et le…
Variations de fonctions et extremums : cours de maths en 2de
56
Un cours sur les variations de fonctions et les extremums en 2de avec la croissance et décroissance d'une fonction ainsi que le tableau de variation. Nous étudierons, dans cette leçon en seconde, l'aspect algébrique puis l'aspect graphique de l'étude des variations d'une fonction. Les connaissances de collège nécessaires pour aborder…
Fonctions : exercices de maths en 2de corrigés en PDF.
55
Des exercices en seconde (2de) sur les généralités sur les fonctions. L'intégralité de ces fiches d'exercices sont corrigés. Exercice n° 1 : Etablir le tableau de signe des expressions algébriques suivantes : a. b. c. Exercice n° 2 : 1. Etablir le tableau de signe de l'expression algébrique suivante :…