Fonctions : exercices de maths en 2de corrigés en PDF.
Mis à jour le 23 décembre 2025
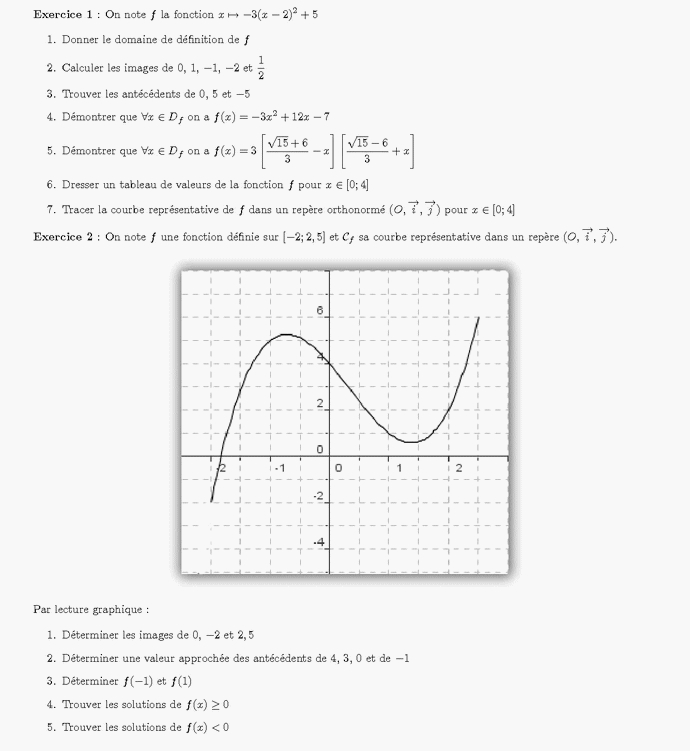
Exercice 1 :
Etablir le tableau de signe des expressions algébriques suivantes :
a. 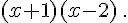
b. 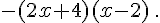
c. 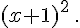
Exercice 2 :
1. Etablir le tableau de signe de l’expression algébrique suivante :
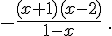
2. Résoudre :
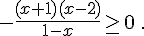
3.
a. Développer 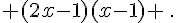 .
.
b. Résoudre :
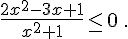 .
.
Exercice 3 :
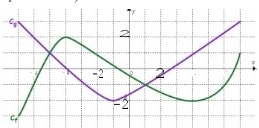
1. Considérons les courbes représentatives des fonctions f et g suivantes :
a. Résoudre 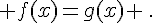 .
.
b. Résoudre 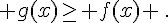 .
.
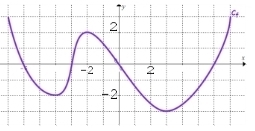
2. Considérons la courbe représentative de la fonction f suivante :
Résoudre les équations et inéquations suivantes :
a. 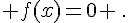 .
.
b.  .
.
c. 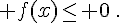 .
.
Exercice 4 :
On considère les fonctions f et g définies par :
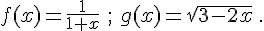 .
.
1. Déterminer l’ensemble de définition de ces deux fonctions.
2. Déterminer l’image de 3 et -1,5 par ces fonctions.
3. Calculer 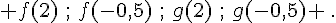 ..
..
4. Déterminer les antécédents de 4 par ces deux fonctions .
Exercice 5 :
On considère la fonction g définie par :
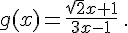 .
.
1. Déterminer l’ensemble de définition de la fonction g .
2. Déterminer les antécédents de 2 par la fonction g (donner les résultats sous forme simplifiée).
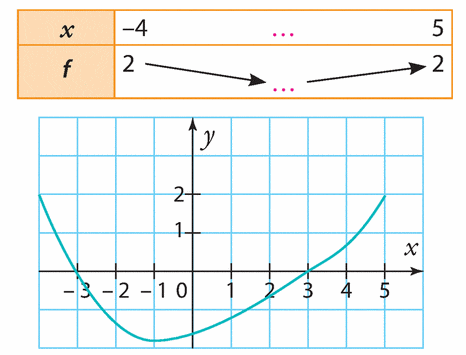
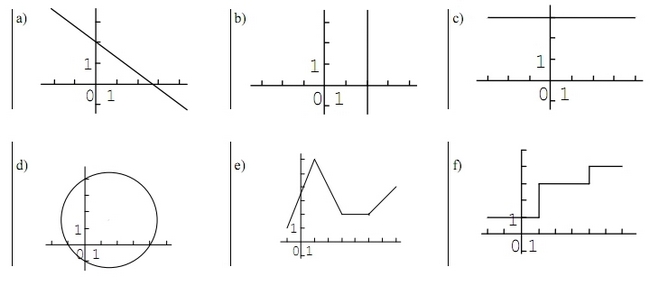
Exercice 6 – Représentation graphique
Pour chacune des courbes ci-dessous, indiquer si c’est la représentation graphique d’une fonction.
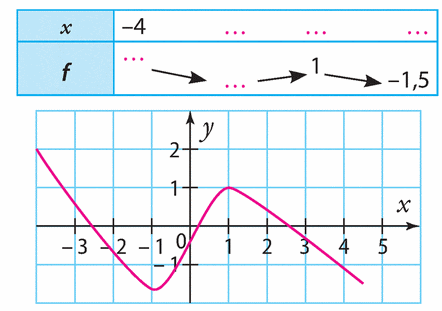
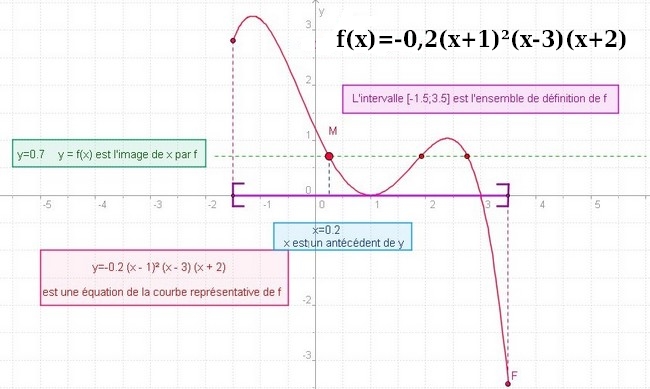
Exercice 7 – Image et antécédent
1. Déterminer par lecture graphique les images de 1et de 2.5 par la fonction f. (à 0.1 près)
2. Retrouver les valeurs exactes de ces résultats par le calcul.
3. Déterminer graphiquement les antécédents de 1. ( toujours à 0.1 près)
4. Résoudre graphiquement l’équation f(x) =0.
5. Résoudre graphiquement l’inéquation f(x)> 1.
Exercice 8 – Fonctions et calcul littéral
On donne
f(x) = 9x² – 4 + (3-2 x) (3x-2) et g (x) = x² +2x +1 – (2x-3)²
1. Développer, réduire et ordonner f(x) et g (x). (1 pt)
2. Factoriser f (x) et g (x).
Soit la fonction rationnelle définie par h(x) = (f(x))/(g(x))
1. Déterminer la condition d’existence de h(x).
2. Simplifier h(x).
3. Résoudre les équations et inéquations suivantes :
h(x) = 0 ; h(x) = 3 et h(x) < 0.
Exercice 9 – Etude d’un rectangle et fonction numériques
 et
et  désignent des réels strictement positifs .
désignent des réels strictement positifs .
Un rectangle de dimension  et
et  (en centimètres) a pour aire
(en centimètres) a pour aire 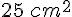 .
.
a) Exprimer  en fonction de
en fonction de  .
.
b) On définit une fonction en associant à la dimension  ,
,
l’autre dimension  .
.
Quel est l’ensemble de définition de cette fonction ?
Exercice 10 – Tableau de signe et étude d’une fonction
f est la fonction définie sur  par
par 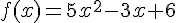 .
.
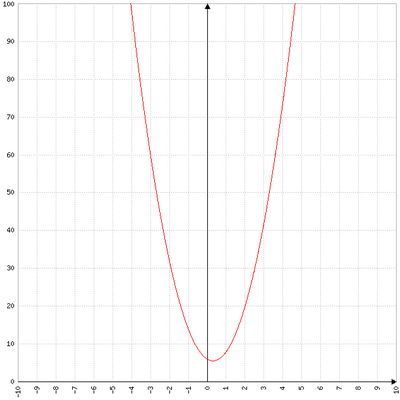
1- Démontrer que, pour tout nombre réel x, 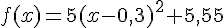 .
.
2- Résoudre graphiquement l’inéquation 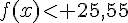 .
.
3- Factoriser 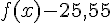 et retrouver les solutions de l’inéquation à l’aide d’un tableau de signes.
et retrouver les solutions de l’inéquation à l’aide d’un tableau de signes.
Exercice 11 – Etude d’une fonction numérique
Soit f la fonction définie sur R par f(x) = 4x² + 16x + 7
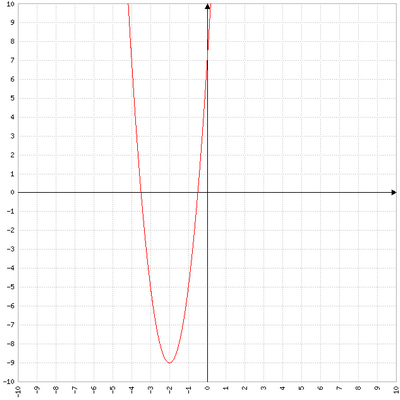
1) démontrer que f(x) = 4(x+2)²-9
2) factoriser f(x)
3) choisir la forme la mieux adaptée et détailler les calcules pour calculer f(-1/2) et f(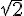 )
)
4) Dans le repère suivant tracer la représentation graphique de f
5 ) résoudre algébriquement f(x) = 0. Expliquer comment contrôler les solutions sur le graphique
6a) résoudre algébriquement l’équation f(x) = 2x+7
b) résoudre graphiquement la même équation
7) quelle forme de f(x) permet d’affirmer que f(x) est toujours supérieur ou égal a -9.
Démontrer alors que pour tout x de R, f(x) est toujours supérieur ou égal a -9.
Comment contrôler ce résultat sur le graphique ?
Exercice 12 – Exercices sur les fonctions
1. On considère les fonctions f, g , h définies sur 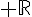 par :
par :
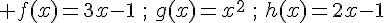 .
.
a. Donner l’expression algébrique de la fonction composée i=hofog .
b. Calculer l’image de -1;0 et 1 par la fonction i .
c. Calculer les antécédents de 27 par i.
2. Décomposer les fonctions suivantes à l’aide des fonctions de référence (fonctions usuelles).
a. 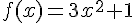 .
.
b. 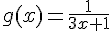 .
.
c. 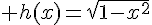 .
.
d. 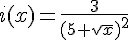 .
.
Exercice 13 :
On considère la fonction f définie sur 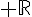 par :
par :
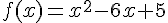 .
.
1. Montrer l’égalité des expressions algébriques suivantes :
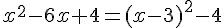
2. On considère, désormais, la fonction f définie par 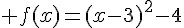 :
:
a. f=hokom avec 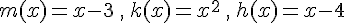
b. Déterminer le sens de variation de la fonction f sur chacun les intervalles ![]-\infty\,;\,3]](https://mathovore.fr/latex-images/10c43c736faca91e476acb0b59cb3aa9.png) et
et 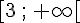 .
.
c. Dresser le tableau de variation de la fonction f sur 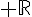 .
.
d. En déduire la valeur minimale de f sur 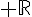 , en quel point est-elle atteinte?
, en quel point est-elle atteinte?
e. Retrouver le résultat de la question d. à l’aide de l’expression algébrique de f.
Exercice 14 – Vocabulaire sur les fonctions
Traduire les phrases suivantes à l’aide d’égalités :
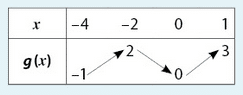
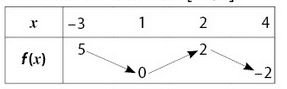
a. Par la fonction g, – 5 est l’image de 4.
b. 2 a pour image 0 par la fonction f.
c. Un antécédent de – 3 par h est 5.
d. Les images par f de – 3 et 5 sont nulles.
Exercice 15 – Etude de deux fonctions numériques
Soient f et g deux fonctions définies sur  par :
par :
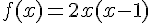 et
et 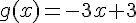 .
.
1. Tracer à l’écran de la calculatrice les courbes représentatives des fonctions
f et g.
2. Conjecturer graphiquement les solutions de l’équation 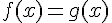 .
.
3. Résoudre algébriquement l’équation 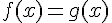 .
.
4. En déduire les coordonnées des points d’intersection des deux courbes.
Exercice 16 – Développer et réduire l’expression de la fonction
Développer, puis réduire, l’expression de la fonction définie sur
définie sur 
par :
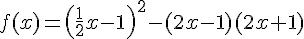
Exercice 17 – Fonctions et géométrie
Soit ABCD un carré de côté 20
Soit M un point de [AB]. On note x la distance AM
Les points P et N sont définis tel que AMNP soit un carré et P appartient à [AD]
Soit f(x) l’aire du carré AMNP et g(x) l’aire du triangle DNC
1. Exprimer f(x) en fonction de x
2. Exprimer g(x) en fonction de x
3.Représenter dans un même repère les fonctions f et g pour tout x de [0;20]
4.Déterminer graphiquement les valeurs de x pour lesquelles le carré AMNP et le triangle DNC ont la même aire
Exercice 18 – Etude d’une fonction
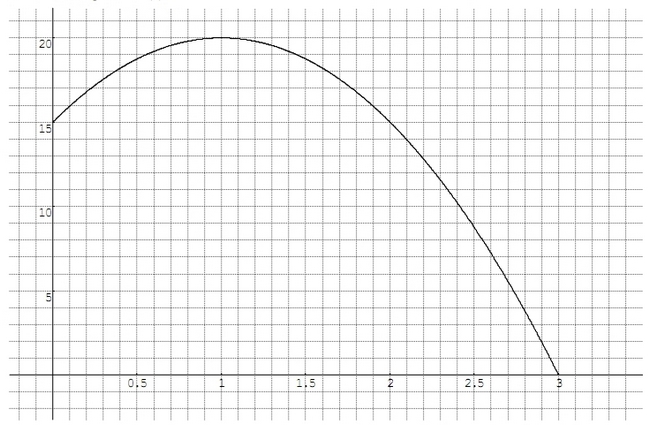
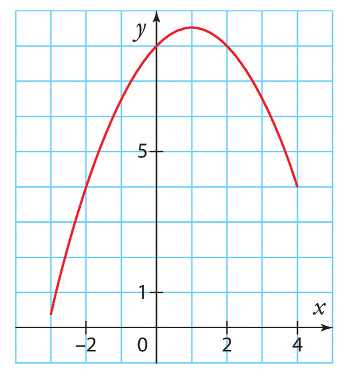
La trajectoire d’une balle de jeu est donné par f(x) = – 5 x² + 10 x + 15 .
où x est le temps écoulé depuis le lancement en l’air, exprimé en secondes, avec x ∈ [0 ; 3],
et f(x) est la hauteur de la balle au dessus du sol, exprimée en mètres .
Partie A. Lecture graphique.
On a représenté graphiquement la fonction f ci-dessous .
Répondre aux questions suivantes en utilisant le graphique.
1° a) Quelle est la hauteur de la balle après 10 secondes ?
b) A quelle hauteur était la balle quand elle a été lancée ?
c) La balle peut-elle être lancée à 20 m ?
d) Au bout de combien de temps est-elle revenue au sol ?
e) Déterminer f(3) et f(0). Que représente ce nombre ?
2° a) Quelle est la hauteur maximale atteinte par la balle
b) Donner les instants où la hauteur est égale à 15 m
c) Résoudre graphiquement f(x) 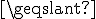 18. Donner une interprétation concrète de cette inéquation.
18. Donner une interprétation concrète de cette inéquation.
Partie B : Calculs .
1° Par le calcul retrouver les résultats de la partie A 1° b) et 1° d
2° a) Démontrer que pour tout réel x de [ 0 ; 3 ], 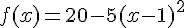 .
.
b) Résoudre l’équation : f(x) = 15. Quel résultat de la partie A retrouve-t-on ?
3° Démontrer que pour tout réel x de [ 0 ; 3 ], f(x) 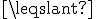 20.
20.
Quel résultat de la partie A retrouve-t-on ?
4° calculer 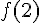 et
et 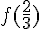 .
.
5° Résoudre l’équation : f(x) = 0.
Exercice 19 :
Soit la fonction linéaire 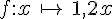 .
.
a. Calculer f(5) ; f(- 1,2) ; f(0) ; f(100).
b. Calculer les nombres x dont les images sont 2 400 ; – 45.
Exercice 20 :
Soit g la fonction linéaire telle que 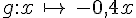 .
.
a. Quel est le coefficient de la fonction g ?
b. Calculer les images de 10 ; – 5 et 1.
c. Compléter les égalités suivantes :
g (10)= … g (- 5 ) = … et g(……)= – 0,4.
Exercice 21 :
On sait que 18 a pour image 23 par la fonction f et que 12 a pour image 14 par f.
f est-elle une fonction linéaire ?Pourquoi ?
Exercice 22 :
Exprimer la fonction linéaire f sous la forme 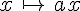 ( le nombre a est à déterminer), puis calculer f(0) ; f(1) et f( – 2).
( le nombre a est à déterminer), puis calculer f(0) ; f(1) et f( – 2).
1. Lorsque l’image de 10 est – 3.
2. Lorsque f (- 100)= – 46.
3. Lorsque le coefficient de f est 2,5.
Exercice 23 :
Dans un repère,
a. Tracer la droite d représentant la fonction 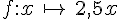
b. Tracer la droite d d’équation 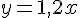 .
.
Quelle fonction la droite d représente-t-elle ?
c. Tracer la droite d’ représentant la fonction linéaire g de coefficient a = – 2.
Exercice 24 :
Expliquer ce que signifie les notations suivantes :
a. 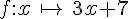 .
.
b. 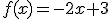 .
.
Exercice 25 :
Parmi les fonctions données, indiquer celles qui sont affines, celles qui sont linéaires, celles qui ne sont pas affines.
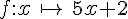
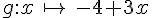
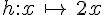
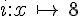
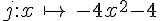
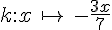
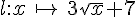
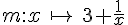
Exercice 26 :
La fonction f est définie par : 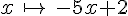 .
.
a. Calculer f(2) ;f(- 3) ; f(0).
b. Calculer l’image de 4.
c. Calculer le nombre x tel que :
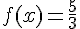 .
.
Exercice 27 :
On donne les images de deux nombres par une fonction affine f.
f(3)=5 et f(7)=13
a. Tracer sa représentation graphique dans un repère.
b. Déterminer l’expression algébrique de cette fonction 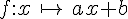 (c’est-à-dire déterminer a et b).
(c’est-à-dire déterminer a et b).
Exercice 28 – Problèmes
1. Dans un magasin, 100 g de chocolats sont vendus 3 €, et l’emballage coûte 1,52 €.
Sonia a acheté 750 g de chocolats et Samy en a achetés 900 g.
Combien chacun a-t-il payé ?
2. Deux personnes sont abonnées à un même ciné-club .
Pour trois séances, la première a payé 16 € (places et abonnement) ; pour cinq séances, la deuxième a payé 22 € ( places et abonnement).
Calculer le prix d’une place et le montant de l’abonnement.
Exercice 29 – Généralités sur les fonctions
Exercice 30 – Etude d’une fonction
Exercice 31 – Sens de variation
Exercice 32 – Tableau de variation
Exercice 33 – Etude d’une fonction rationnelle
On considère la fonction f définie par  .
.
1. Déterminer son ensemble de définition.
2. Démontrer que f est une fonction positive sur  .
.
3. Etudier la parité de la fonction f.
4. Tracer soigneusement la représentation graphique Cf de la fonction f.
5. Donner par lecture graphique la valeur du maximum de f sur :
a. l’intervalle [- 1;1].
b. l’intervalle [- 2;1].
6. Résoudre l’inéquation  .
.
Exercice 34 – Image et antécédent
Soit  définie sur
définie sur  par
par 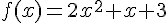
1. Calculer l’image de 0, l’image de 1 et l’image de 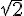 par la fonction
par la fonction  .
.
2. Déterminer le (ou les) antécédent(s) de 3 par  .
.
Exercice 35 – Image et antécédent par une fonction
 est la fonction définie sur
est la fonction définie sur  par :
par :
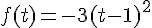 .
.
1. Calculer l’image de 2.
2. Calculer 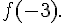
3. Est-il vrai que 4 n’admet pas d’antécédent par  ?
?
4. Est-il vrai que 0 admet un seul antécédent par  ?
?
5. Déterminer un antécédent de – 12 .
Exercice 36 – Domaine de définition, image et antécédent
 est la fonction définie sur
est la fonction définie sur ![]-2;+\infty[](https://mathovore.fr/latex-images/c878284574639705d6c952cfb80fd622.png) par :
par :
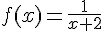
1. Expliquer pourquoi  n’est pas définie en
n’est pas définie en  .
.
2. Calculer 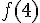 .
.
3. Déterminer l’antécédent de 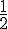 .
.
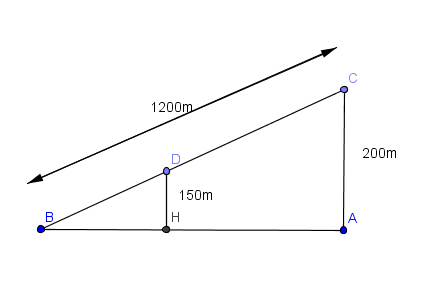
Exercice 37 – Skieur et théorème de Thalès
Un skieur dévale, tout schuss, une piste rectiligne représentée ci-dessous par le segment [BC] de longueur 1 200 m.
A son point de départ C, le dénivelé par rapport au bas de la piste, donné par la longueur AC, est de 200 m. Après une chute, il est arrêté au point D sur la piste.
Le dénivelé donné par la longueur DH, est alors de 150 M.
Calculer la longueur DB qu’il lui reste à parcourir.
Exercice 38 – Problème sur les fonctions
On fabrique une boîte à partir d’une feuille de carton carrée de 18 cm de côté .
On découpe à chaque coin du carré, un carré de côté x (cm) et on plie à 90° les bords libérés de façon à former une boîte de profondeur égale à x (cm).
On note x la largeur de l’encoche exprimée en cm, f(x) le volume de la boîte exprimée en cm cube.
1) Donner les valeurs possibles de x.
En déduire l’ensemble de définition D de f.
2) Donner l’expression de f sur D.
3) Représenter graphiquement cette fonction.
4) A l’aide du graphique, donner la valeur de x pour laquelle le volume de la boîte est maximal et établir le tableau de variations de la fonction f.
5) Montrer que f(x) – f(3) = 4 (x – 3)² (x – 12).
En déduire que f(x) est inférieur ou égal à f(3) pour tout x élément de [0;9]. Que peut-on en conclure ?
Exercice 39 :
Soit f la fonction définie sur  par
par 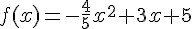
1)a) Calculer l’image de 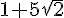 par f , on donnera le résultat sous la forme
par f , on donnera le résultat sous la forme 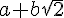 avec a et b deux décimaux .
avec a et b deux décimaux .
b) Reprendre la question précédente avec 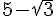 .
.
2) Déterminez les antécédents de 5 par f.
3) a)Démontrez que pour tout x réel on a 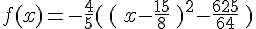 .
.
b) En déduire l’expression factorisée de f(x).
c) Déterminez alors les antécédents de 0 par f
Exercice 40 :
On considère la fonction f définie sur  par:
par:
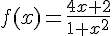 .
.
1. A-t-on f(3) = 1 ?
2. Les images de 2 et de 0 par f sont-elles égales ?
3. Déterminer l’image de 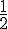 par f.
par f.
4. Déterminer les antécédents de 0 par f.
Exercice 41 :
Voici la courbe représentative d’une fonction f définie sur  .
.
Par lecture graphique, déterminer :
a) l’image de -1 par f.
b) l’image de 0 par f.
c) le (ou les) antécédent(s) de 1 par f.
d) le (ou les) antécédent(s) de 3 par f.
Exercice 42 :
Voici la courbe représentative d’une fonction g définie sur [-2 ; 3].
Par lecture graphique, déterminer :
a) g(0).
b) les images de 1 et -2 par g.
Exercice 43 :
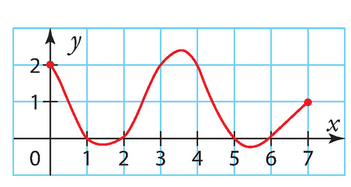
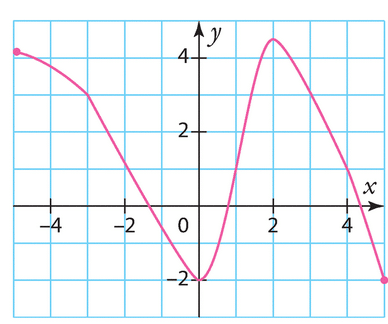
Voici la courbe représentative d’une fonction f définie sur [0;7].
Estimer les solutions des équations suivantes.
a) f(x)= 2 b) f(x)=0 c) f(x) = – 1 d) f(x) = 1.
Exercice 44 :
Voici la courbe représentative d’une fonction g définie sur [-5 ; 5].
Estimer les solutions des équations.
a) g(x) = 2.
b) g(x)= -3.
c) g(x) =4.
d) g(x) = -1.
Exercice 45 :
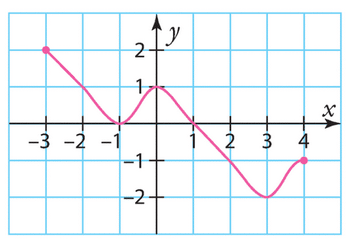
Voici la courbe représentative d’une fonction k définie sur [-3 ; 4].
Estimer les solutions des équations et inéquations suivantes.
a) k(x) =1 b) k(x) = 0 c) k(x)> -1
d) k(x) < 0 e) k(x) 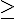 -2 f) k(x)
-2 f) k(x) 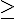 2
2
Exercice 46 :
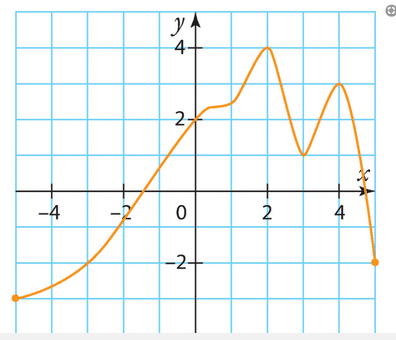
Voici la courbe représentative d’une fonction h définie sur [-5 ; 5].
Estimer les solutions des inéquations suivantes.
a) h(x) 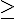 0
0
b) h(x) < -4
c) h(x) < -2
d) h(x) > 2
Exercice 47 :
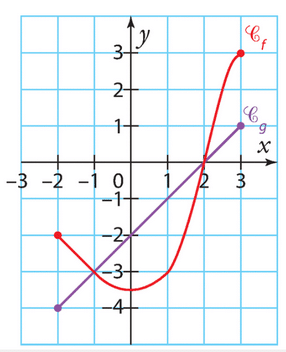
Voici les courbes représentatives d’une fonction f
et d’une fonction g définies sur [-2;3].
Résoudre graphiquement les équations et inéquations.
a) g(x) = f(x)
b) g(x) 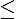 f(x)
f(x)
c) f(x) < -3
d) g(x) < 2
e) f(x) 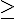 -2
-2
Exercice 48 :
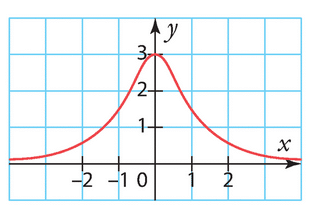
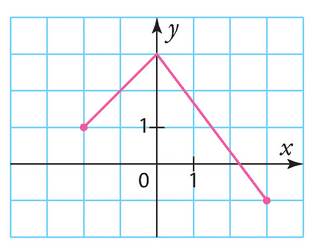
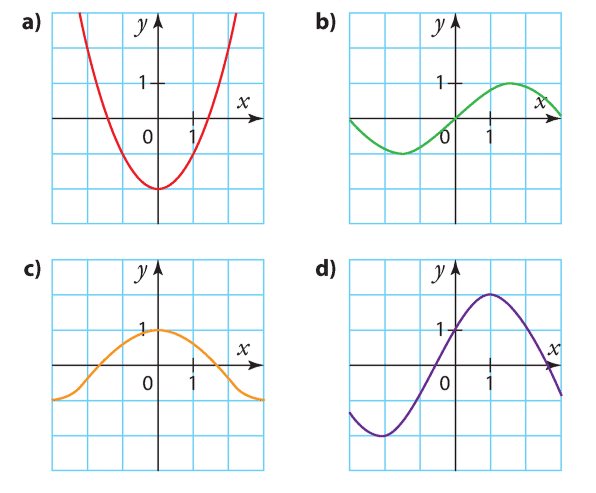
Pour chacune des courbes ci-dessous, dire si elle semble être la courbe représentative d’une fonction paire, d’une fonction impaire ou d’une fonction qui n’est ni paire ni impaire.
Exercice 49 :
Pour chacune des fonctions dont on donne les expressions ci-dessous,
essayer d’établir le plus grand ensemble de définition possible.
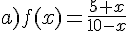
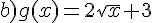
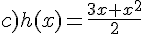
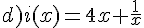
Exercice 50 :
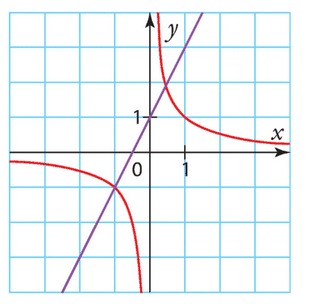
On considère les courbes représentatives de la fonction inverse, notée f,
et de la fonction affine g définie sur R par g(x) = 2x + 1.
Elles sont tracées dans le repère ci-dessous.
1. Repérer les courbes associées aux deux fonctions.
2. Résoudre graphiquement l’équation 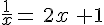 .
.
3. a) Développer l’expression (2x – 1)(x+ 1).
b) Retrouver algébriquement les résultats obtenus à la question 2.
Exercice 51 :
On considère une fonction f dont on donne la représentation graphique sur [3;4].
1. Déterminer l’image de 2.
2. Donner la valeur de f(-2).
3. Donner une valeur approchée des antécédents de 5.
4. Résoudre f(x) = 4.
5. Résoudre f(x) < 6.
6. Résoudre f(x) 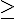 8.
8.
Exercice 52 :
Soit f la fonction définie par 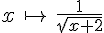
1) Déterminer Df, l’ensemble de définition de f.
2) Déterminer les images de –1, 7 et –4.
3) Déterminer graphiquement le ou les antécédents de 2.
4) Déterminer par le calcul le ou les antécédents de –1.
5) Représenter graphiquement f.
Exercice 53 :
Soit la fonction f définie par 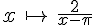
1) Déterminer l’ensemble de définition de f.
2) Déterminer les images de 0 et 2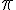 .
.
3) Déterminer le ou les antécédents de 2 et 0.
4) Déterminer le signe de f.
5) Tracer la représentation graphique de f.
Exercice 54 :
On définit la fonction f sur ℝ par 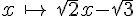
1) Calculer l’image de 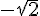 .
.
2) Déterminer le ou les antécédents de 0 et 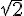 .
.
3) Étudier le signe de f.
4) Tracer la courbe Cf.
Exercice 55 :
Soit f la fonction définie sur  par :
par :
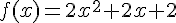
1) Déterminer le signe de f.
2) f admet-elle un extrémum ?
3) Représenter graphiquement f.
Exercice 56 :
Soit f la fonction définie sur ]–3 ; +∞[ par 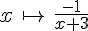
1) Étudier le signe de f.
2) Étudier les variations de f.
3) Tracer la courbe Cf.
Exercice 57 :
f est la fonction définie sur ℝ par 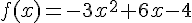
1) Déterminer le ou les antécédents de –1, –4 et 0
2) Déterminer le signe de f.
3) Montrer que f admet un extremum que l’on caractérisera.
4) Étudier les variations de f.
5) Représenter graphiquement f.
Exercice 58 :
Soit f la fonction définie par 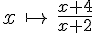
1) Déterminer Df.
2) Calculer les images de 0 et 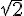 .
.
3) Étudier les variations de f.
4) Représenter graphiquement f.
5) Résoudre graphiquement : f (x) = 3.
6) Résoudre graphiquement : f (x) > x.
Exercice 59 :
Soient f : 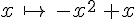 et g :
et g : 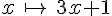 .
.
1) Étudier les variations de f. puis celles de g.
2) Représenter graphiquement ces deux fonctions
3) Déterminer la position relative de Cf et Cg.
Exercice 60 :
Déterminer le sens de variation des fonctions ci-dessous:
1) x  (x + 1)2 − 5 sur ]−
(x + 1)2 − 5 sur ]− ; −1]
; −1]
2) x 
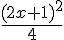 sur ]−
sur ]− ; −1/2]
; −1/2]
3) x 
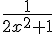 sur R−
sur R−
4) x  2 +
2 + 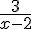 sur ]2 ; +
sur ]2 ; + [
[
5) x 
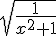 sur R+
sur R+
6) x  (| x | + 1)2 sur R−
(| x | + 1)2 sur R−
7) x  3 +
3 + 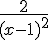 sur ]1 ; +
sur ]1 ; + [
[
8) x 
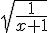 sur ]−1 ; +
sur ]−1 ; + [
[
9) x 
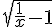 sur ]0 ; 1]
sur ]0 ; 1]
10) x 
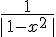 sur [0 ; 1[
sur [0 ; 1[
Exercice 61 :
Décrire le sens de variation de la fonction définie par la courbe donnée.
Exercice 62 :
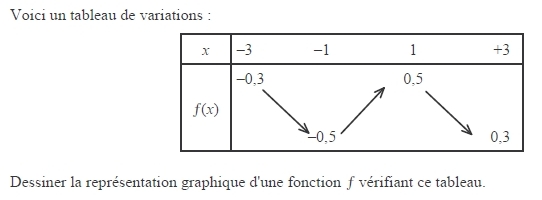
Décrire le sens de variation de la fonction dont voici le tableau de variation.
Exercice 63 :
Le tableau ci-dessous donne le sens de variation d’une fonction f définie sur l’intervalle [-3;4].
Pour chaque affirmation, dire si elle est vraie ou fausse. Justifier votre réponse.
1.f est croissante sur [0;2].
2.f est décroissante sur [-1;1].
3.f(3)>f(2).
4.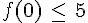
5.Pour tout nombre réel x de l’intervalle [-3;2], 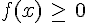 .
.
Exercice 64 :
f est une fonction définie sur l’intervalle [-3;6] telle que :
- le maximum de f sur [-3;6] est égal à 5, il est atteint pour x=0.
- le minimum de f sur [-3;6] est égal à -2, il est atteint pour x=3.
- les antécédents de 0 par f sont atteints pour x=0;-3 et 6.
- le maximum de f sur [-3;-1] est égal à 3 et il est atteint pour x= – 2.
- f(-1)=2 et f est croissante sur [-1;0].
Tracer une courbe susceptible de représenter la fonction f dans ce repère.
Exercice 65 :
g est une fonction décroissante sur  telle que g(0)=1 et g(1)=0.
telle que g(0)=1 et g(1)=0.
Quel est l’ensemble des nombres réels tels que :
a) 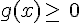
b) g(x)<1.
Exercice 66 :
Les questions 1. à 5. Comportent trois réponses possibles. Pour chacune de ces questions, une seule des réponses proposées est exacte. On demande de cocher cette réponse.
Une réponse inexacte enlève la moitié des points attribués à la question. L’absence de réponse à une question ne rapporte aucun point et n’en enlève aucun. Si le total est négatif, la note est ramenée à 0.
Soit f une fonction définie sur l’intervalle [-5;5] dont le tableau de variation est le suivant :(on suppose que la courbe représentative de f sur [-5;5] s’obtient « sans lever le crayon »)
|
|
|
|
|
|
|
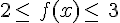 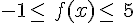 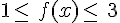 |
|
|
Exercice 67 :
Une joueuse de handball lance une balle devant elle.
Au bout de x mètres parcourus, la hauteur de la balle (en mètres) avant qu’elle ne touche
le sol est donnée par : 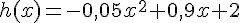 .
.
Quelle est la hauteur de la balle après 20 mètres parcourus ?
Que peut-on en déduire pour la balle ?s
a) Montrer que 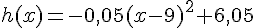 .
.
b) Que peut-on dire du signe de 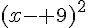 ?
?
c) En déduire la hauteur maximale atteinte par la balle.
Exercice 68 :
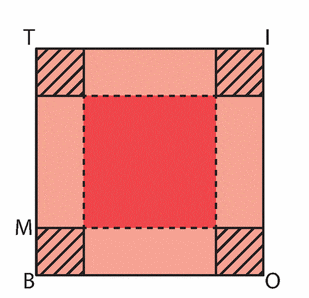
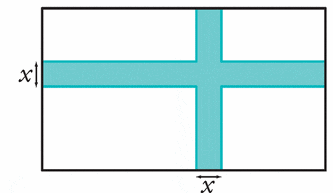
On considère un rectangle de longueur 7 et de largeur 5.
On trace à l’intérieur de celui-ci une croix de largeur x
variable comme indiqué ci-dessous.
On s’intéresse à l’aire de la croix bleue.
1. A quel intervalle x appartient-il ?
2. Exprimer l’aire 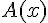 de la croix bleue en fonction de x.
de la croix bleue en fonction de x.
3. Avec la calculatrice, dresser le tableau de valeurs de 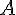 avec un pas de 1.
avec un pas de 1.
Exercice 69 :
Le prix de l’essence sans plomb est de 1 euro le litre.
Marius veut faire le plein de sa voiture. II compte mettre x litres dans
son réservoir vide qui peut contenir 40 litres.
La station dans laquelle il se sert ne délivre pas moins de 5 litres.
On considère la fonction P qui à chaque valeur de x associe
le prix payé par Marius.
1. D’après le contexte de l’exercice, à quel intervalle x appartient-il ?
2. Quel est l’ensemble de définition de la fonction P ?
3. Déterminer l’expression algébrique de la fonction P.

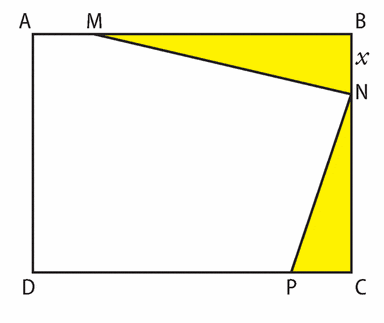
Exercice 70 :
ABCD est un rectangle tel que AB 10 cm et BC = 8 cm.
N est un point mobile sur le segment [BC].
On note x la longueur en centimètres M et P sont les points respectifs de [AB] et [CD] tels que
AM = BN = CP = x.
Le but de cet exercice est de déterminer où placer N sur le segment [BC] pour que l’aire de la surface jaune, la somme des aires des triangles BMN et CNP, soit maximale.
1. Justifier que ![x \in [O ; 8]](https://mathovore.fr/latex-images/cd11eba503a73843e570462fd5de5559.png) .
.
2. Exprimer BM en fonction de x.
3. Exprimer CN en fonction de x.
4. Montrer que l’aire du triangle BMN est égale à
5. On note f la fonction qui à la longueur x associe l’aire totale de la surface jaune.
Vérifier que l’on a 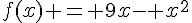 .
.
6.a) Montrer que 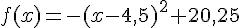 .
.
b) En déduire la solution au problème posé.
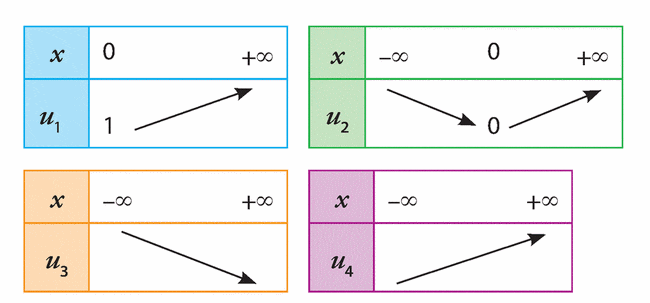
Exercice 71 :
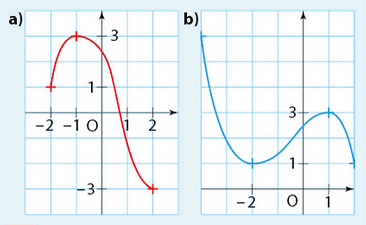
Associer chaque fonction son tableau de variations
parmi les suivants.
a) f définie sur  par f(x) = —2x+ 4.
par f(x) = —2x+ 4.
b) g définie sur  par g(x) =
par g(x) = 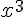 .
.
c) h définie sur  par h(x) =
par h(x) = 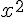 .
.
d) k définie sur  par k(x) =
par k(x) = 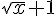 .
.
Exercice 72 :
Une fonction f possède les propriétés suivantes :
• elle est définie sur [—3 ; 5] ;
• elle est croissante sur [—3 ; —I] ;
• elle est décroissante sur [—1 ; 4] ;
• elle est croissante sur [4 ; 5] ;
• sur l’intervalle [—3 ; 4], son maximum vaut 6 ;
• sur l’intervalle [-1 ; 5], son minimum vaut -3 ;
• l’image de —3 est I ;
• 5 est un antécédent de 7.
Dresser le tableau de variations de cette fonction.
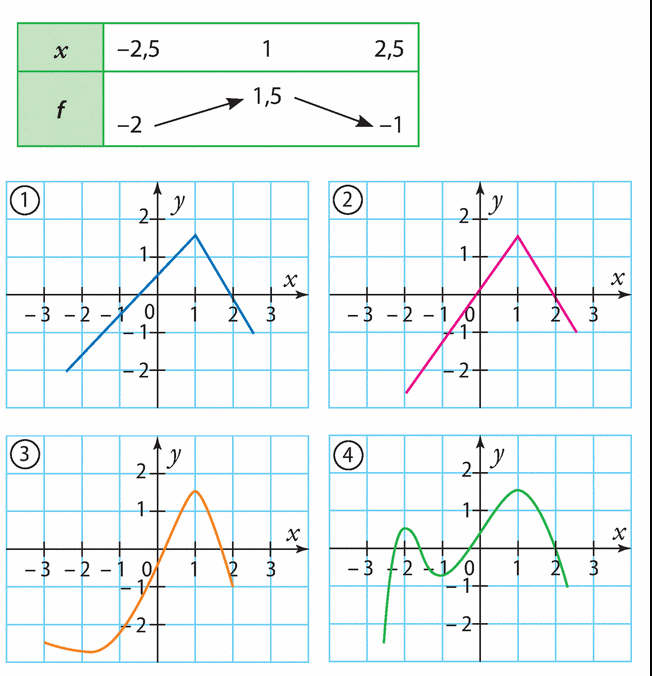
Exercice 73 :
Exercice 74 :
Voici le tableau de variations d’une fonction f.
Comparer si possible les nombres suivants en justifiant.
1. a) f(2) et f(4).
b) f(- 2) et f(- 1).
2. Résoudre 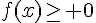 .
.
3. On sait de plus que 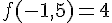 .
.
Résoudre 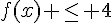 et
et 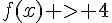 .
.
Exercice 75 :
On considère un carré de côté 15 cm.
Dans chaque coin, on découpe un même carré pour obtenir un patron d’une boite sans couvercle.
A. Un cas particulier
1. Construire le patron d’une boite en choisissant BM = 3 cm.
2.Calculer son volume.
3. Peut-on réaliser une boîte sachant que BM = 8 cm ?
Expliquer.
B. Une fonction
On pose BM= x et on appelle V la fonction qui à x associe le volume de la boite sans couvercle.
1. Déterminer une expression de la fonction V.
2. Quel est l’ensemble de définition de V ?
3. A l’aide d’une calculatrice, ou d’un logiciel, tracer la courbe représentative de la fonction V.
4. Pour quelles valeurs de x le volume est-il supérieur ou égal 100 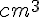 ?
?
5. Le volume de cette boite peut-il dépasser 1 dL ?
Si oui, donner les dimensions d’une boite vérifiant cette condition.
Si non, expliquer pourquoi.
Exercice 76 :
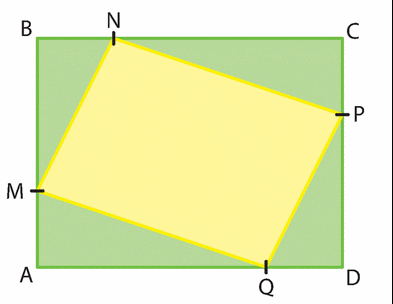
On considère un rectangle ABCD de dimensions AB = 6 cm et BC = 8 cm.
Sur le côté [AB], on place un point M quelconque.
On considère ensuite les points N sur [BC], P sur [CD] et Q sur [DA] tels que
AM = BN = CP = DQ.
On pose AM = x. On appelle f la fonction qui x associe la valeur de l’aire de MNPQ.
1. AM peut-elle prendre la valeur 7 ?
Quel est l’ensemble de définition de f?
2. Démontrer que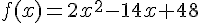 .
.
3. A l’aide d’une calculatrice ou d’un logiciel, tracer la courbe
Représentative de f. Ajuster la fenêtre d’affichage.
4.Pour quelle(s) valeur(s) de x l’aire de MNPQ est-elle supérieure ou égale à 24 cm² ?
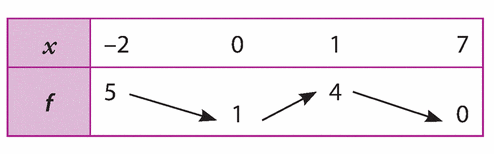
Exercice 77 :
g est une fonction dont on connait le tableau de variations.
a) Donner le sens de variation de la fonction g sur l’intervalle [2 ; 5].
b) En déduire quel est le nombre le plus grand entre g (3) et g(4).
2. Sur le modèle de la question précédente, comparer g (1) et g(l ,5).
3. Même question pour g (—2) et g (O).
Exercice 78 :
Recopier et compléter le tableau de variations proposé à partir de la représentation graphique suivante.
Exercice 79 :
Recopier et compléter le tableau de variations proposé à partir de la représentation graphique suivante :
Exercice 80 :
Recopier et compléter le tableau de variations proposé partir de Ia représentation graphique suivante.
Exercice 81 :
Déterminer a et b pour que le tableau ci-dessous soit un tableau de valeurs d’une fonction h définie par
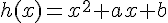 sur
sur  .
.
2. La fonction h est-elle paire ? impaire ?
3. Déterminer les antécédents de —7 par h.
Exercice 82 :
On considère la fonction f définie sur  par f(x) = —2x+ 5.
par f(x) = —2x+ 5.
1. Déterminer le ou les antécédents de —2 par f.
2. Écrire un algorithme ou un programme qui :
— demande une valeur b l’utilisateur ;
— calcule puis affiche le ou les antécédents de b par la
fonction f.
Exercice 83 :
1. A l’aide de la calculatrice, recopier et compléter le tableau de valeurs de la fonction h définie
sur [—2 ; 2] par h(x)=(3x+1)(5-x).
2. Déterminer tous les antécédents de 0 par h.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «fonctions : exercices de maths en 2de corrigés en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.





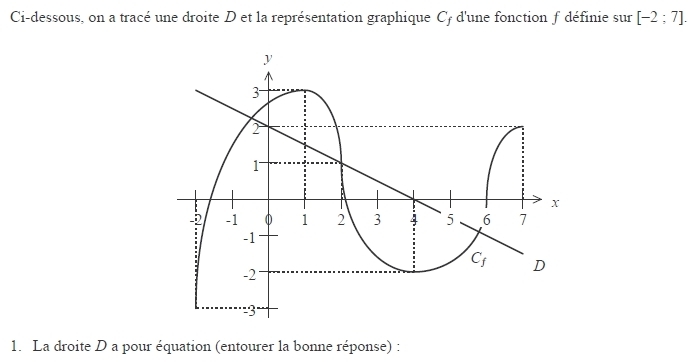



 la courbe représentative de la fonction f dans un repère, alors
la courbe représentative de la fonction f dans un repère, alors 
 , alors
, alors
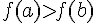
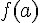 et
et 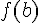 sont négatifs
sont négatifs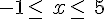 alors
alors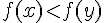
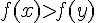
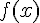 et
et 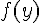 sont de signes opposés
sont de signes opposés