Triangle : corrigé des exercices de maths en 5ème en PDF.

Mis à jour le 28 mai 2025

Sommaire

🔍Corrigés Détaillés

5eme • Scolaire

Triangle

🔎 Analyse : 16 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en 5ème sur les triangles. Savoir tracer un triangle à l’aide du matériel de géométrie. Utiliser l’inégalité triangulaire et tracer le cercle circonscrit à un triangle en cinquième.

Exercice 1 :

1. Soit LNI un triangle tel que : 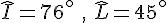$\widehat{I}=76^{\circ}\,\,,\,\,\widehat{L}=45^{\circ}$

Calculer la mesure de l’angle 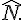$\widehat{N}.$

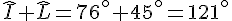
$\widehat{I}+\widehat{L}=76^{\circ}+45^{\circ}=121^{\circ}$

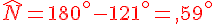
$\widehat{N}=180^{\circ}-121^{\circ}={\color{DarkRed},59^{\circ}}$

2. Soit SAC un triangle tel que 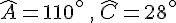$\widehat{A}=110^{\circ}\,,\,\widehat{C}=28^{\circ}$

Calculer la mesure de l’angle 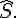$\widehat{S}.$

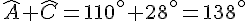
$\widehat{A}+\widehat{C}=110^{\circ}+28^{\circ}=138^{\circ}$

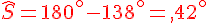
$\widehat{S}=180^{\circ}-138^{\circ}={\color{DarkRed},42^{\circ}}$

Exercice 2 :

Exercice 3 :

Exercice 4 :

ACD est un triangle équilatéral donc ses trois angles mesurent 60°.

ACE est un triangle rectangle isocèle donc 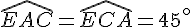$\widehat{EAC}=\widehat{ECA}=45^{\circ}$

Ensuite 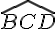$\widehat{BCD}$ est un angle plat donc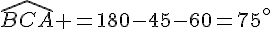 $\widehat{BCA} =180-45-60=75^{\circ}$

Et ABC est isocèle en A donc ses angles à la base ont la même mesure.

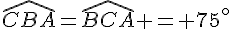
$\widehat{CBA}=\widehat{BCA} = 75^{\circ}$

et le dernier angle mesure :

180-150=30°

Exercice 5 :

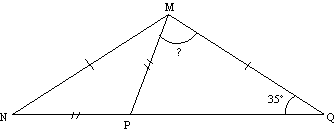
Le triangle MNQ est isocèle de sommet principal M et de base [NQ].

Le triangle PMN est isocèle de sommet principal P et de base [MN].

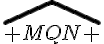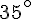L’angle $\widehat{ MQN }$ mesure $35^{\circ}$ .

Déterminer la mesure de l’angle 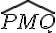$\widehat{PMQ}$ .

MQN est isocèle en M donc les angles à la base sont égaux.

donc

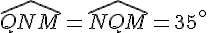
$\widehat{QNM}=\widehat{NQM}=35^{\circ}$

Le trangle NPM est isocèle en P donc les angles à la base ont la même mesure.

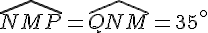
$\widehat{NMP}=\widehat{QNM}=35^{\circ}$

ensuite

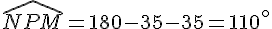
$\widehat{NPM}=180-35-35=110^{\circ}$

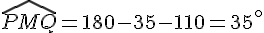
$\widehat{PMQ}=180-35-110=35^{\circ}$

Exercice 6 :

On considère un triangle MNO, isocèle de sommet principal N et de base [MO].

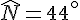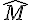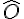On sait que $\widehat{N}=44^{\circ}$ . En déduire la mesure de $\widehat{M}$ et $\widehat{O}$ .

Les angles à la base ont même mesure pour un triangle isocèle.

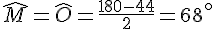
$\widehat{M}=\widehat{O}=\frac{180-44}{2}=68^{\circ}$

Exercice 7 :

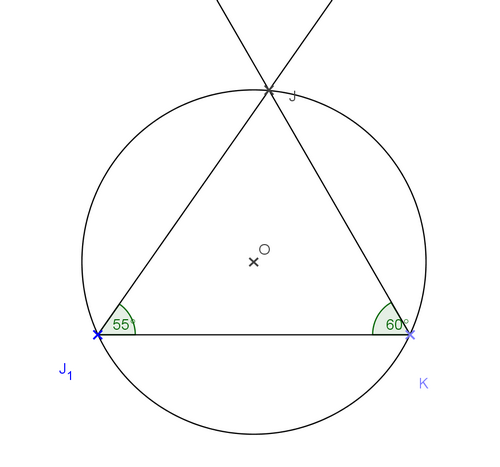
On considère un triangle équilatéral JKL.

En déduire la mesure de ses trois angles.

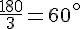
$\frac{180}{3}=60^{\circ}$

les trois angles d’un triangle équilatéral sont mesurent 60 °.

Exercice 8 :

On considère un triangle GHI, rectangle en H. On sait que 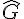$\widehat{G}$ = 34°.

En déduire la mesure de 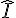$\widehat{I}$ .

$\widehat{I}=180-90-34=56^{\circ}$

Exercice 9 :

Magalie a mesuré les angles DEF avec son rapporteur.

Elle a trouvé 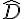$\widehat{D}$ = 53°, 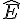$\widehat{E}$ = 74° et 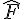$\widehat{F}$ = 54°.

Que penses-tu de sa réponse ? Justifie.

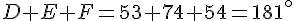
$D+E+F=53+74+54=181^{\circ}$

Les mesures de Magalie sont fausses car la somme des trois angles d’un triangle est de 180°.

Exercice 10 :

On considère un triangle ABC. On sait que 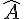$\widehat{A}$ = 28° et 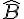$\widehat{B}$ = 73°.

En déduire la mesure de 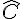$\widehat{C}$ .

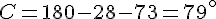
$C=180-28-73=79^{\circ}$

Exercice 11 :

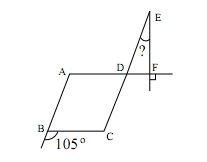
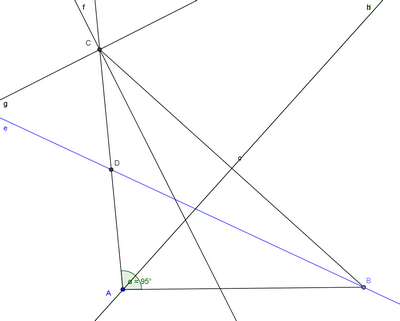
Quelle est la mesure de l’angle DEF ?

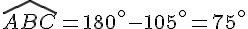
$\widehat{ABC}=180^{\circ}-105^{\circ}=75^{\circ}$

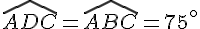$\widehat{ADC}=\widehat{ABC}=75^{\circ}$ (les angles opposés d’un parallélogramme ont la même mesure ) .

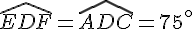$\widehat{EDF}=\widehat{ADC}=75^{\circ}$ (deux angles opposés par le sommet ont la même mesure ).

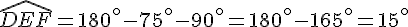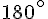$\widehat{DEF}=180^{\circ}-75^{\circ}-90^{\circ}=180^{\circ}-165^{\circ}=15^{\circ}$ (la somme des angles d’un triangle vaut $180^{\circ}$ )

Exercice 12 :

Quelle est la mesure de l’angle ADB ?

Dans le triangle ADC :

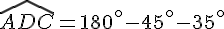
$\widehat{ADC}=180^{\circ}-45^{\circ}-35^{\circ}$

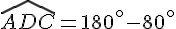
$\widehat{ADC}=180^{\circ}-80^{\circ}$

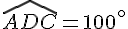
$\widehat{ADC}=100^{\circ}$

L’angle 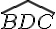$\widehat{BDC}$ est un angle plat .

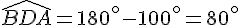
$\widehat{BDA}=180^{\circ}-100^{\circ}=80^{\circ}$

Exercice 13 :

Exercice 14 :

Exercice 16 :

La somme des angles des angles est 180 °.

90°+84,7°=174,7°

180°-174,7°=5,3°

Donc l’angle d’inclinaison par rapport à la verticale est de 5,3 ° .

La somme des angles est un calcul fondamental à maîtriser dans ce chapitre sur le triangle.

Exercice 18 :

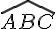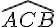Soit ABC un triangle rectangle en A. Montrer que $\widehat{ABC}$ et $\widehat{ACB}$ sont complémentaires.
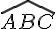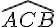$\widehat{ABC}$ + $\widehat{ACB}$ = 180 – 90 = 90° donc ces deux angles sont complémentaires.

Exercice 19 :

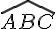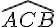Soit ABC un triangle tel que $\widehat{ABC}$ et $\widehat{ACB}$ soient complémentaires. Montrer que ABC est rectangle en A.
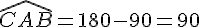$\widehat{CAB}=180-90=90$ donc ABC est rectangle en A.

Exercice 20 :

Soit ABC un triangle isocèle en A et d la médiatrice de [BC].
1) Montrer que A appartient à d.
ABC est isocèle en A donc AB=AC ainsi A est sur la médiatrice du segment [BC]

2) Déterminer les images de A, B et C par la symétrie d’axe d.
3) Montrer que les angles à la base du triangle ABC sont de même mesure.

Exercice 21 :

Soit ABC un triangle isocèle en A et ayant un angle de 60°.
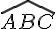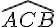1er cas : L’angle de 60° est (BAC) ˆ: Déterminer $\widehat{ABC}$ et $\widehat{ACB}$ . En déduire que ABC est équilatéral.
Les angles à la base ont la même mesure donc 180-60=120 et 120:2=60 °

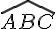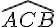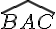2ème cas : L’angle de 60° est $\widehat{ABC}$ : Déterminer $\widehat{ACB}$ et $\widehat{BAC}$ . En déduire que ABC est équilatéral.
3ème cas : L’angle de 60° est 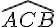$\widehat{ACB}$ : Pourquoi est-il inutile d’étudier ce troisième cas ?

Exercice 22 :

Soit ABC un triangle quelconque et O le point d’intersection des médiatrices de [AB] et de [AC].
1) Montrer que OA = OB puis que OA = OC.
D’après la propriété de la médiatrice comme O appartient à la médiatrice de [AB] alors OA=OB
et comme O appartient à la médiatrice de [AC] alors OA=OC .

2) En déduire que O est le centre du cercle circonscrit au triangle.
Nous avons OA=OB et OA=OC donc par transitivité OA=OB=OC donc le cercle de centre O et de rayon OA passe par les trois sommets du triangle ABC, c’est son cercle circonscrit.

3) En déduire également que O appartient aussi à la médiatrice de [BC]
Comme OB=OC alors O appartient à la médiatrice du segment [BC].

Exercice 23 :

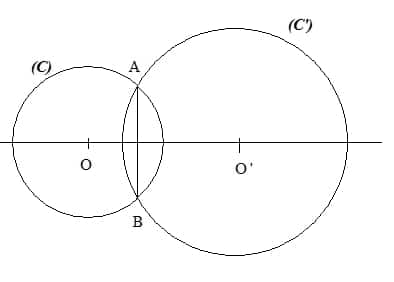
( C ) est un cercle de centre O et de rayon 2 cm.

( C’ ) est un cercle de centre O’ et de rayon 3 cm.

Les deux cercles se coupent en A et B.

Démontre que (OO’) est la médiatrice de [AB].

Nous avons OA=OB car ce sont des rayons du cercle (C)donc O appartient à la médiatrice du segment [AB] et nous avons O’A=O’B car ce sont des rayons du cercle (C’) donc O’ appartient à la médiatrice du segment [AB].

Donc les points O et O’ appartiennent à la médiatrice du segment [AB], par unicité de la médiatrice d’un segment, on en déduit que (OO’) est la médiatrice du segment [AB].

Exercice 24 :

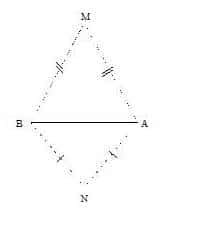
Expliquer pourquoi sur la figure ci-dessous (MN) perpendiculaire à (AB).

M est sur la médiatrice de [AB] et N aussi car MB=MA et NB=NA.

Donc la droite (MN) est la médatrice du segment [AB] ainsi par définition

de la médiatrice d’un segment, on en déduit que (MN) perpendiculaire à (AB).

Exercice 25 :

Tracer un segment [AB].

Construire son milieu I sans utiliser de quadrillage ni d’instrument graduée.

Il suffit de tracer la médiatrice du segment [AB] à la règle non graduée et avec le compas.

Exercice 26 :

On donne une droite (d) et un point N qui n’est pas sur cette droite.

Construire deux points A et B de (d) tel que la médiatrice de [AB] passe par N.

Il faut construire le symétrique N’ par rapport à l’axe (d) et construire le losange NAN’B avec A et B sur D.

Exercice 27 :

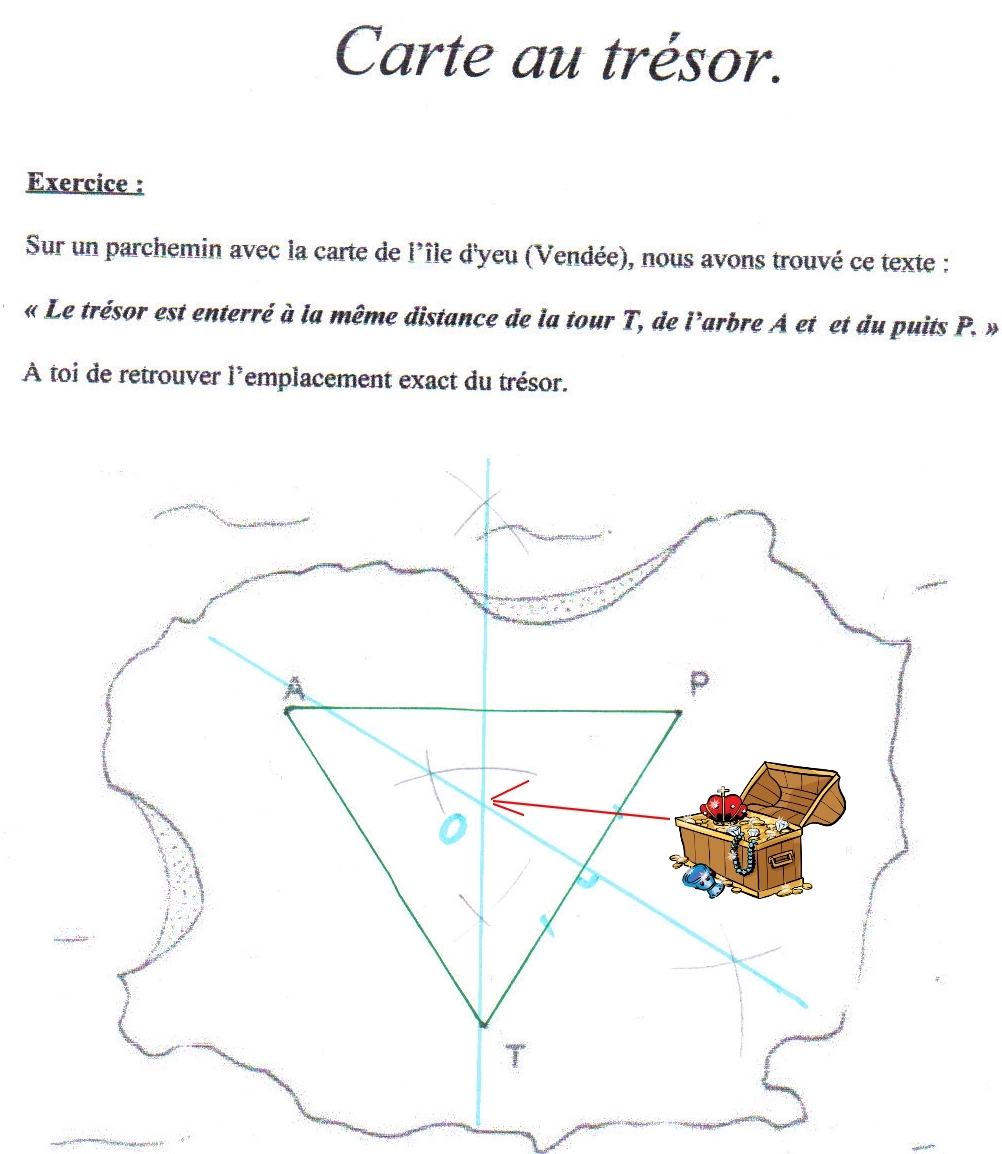
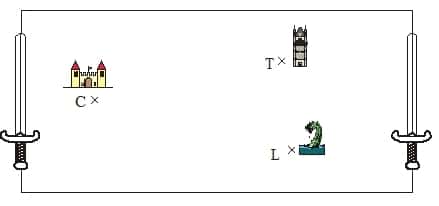
Le bon roi Gatovert a caché son épée magique.

Tu dois la retrouver sur le plan ci-dessous, sachant qu’il l’a enterrée à égale distance de son château C, de la vielle tour T et du lac au dragon L.

Il faut tracer le triangle TLC et deux médiatrices de ce triangle.

Son épée est au point d’intersection de ces deux médiatrices.

Exercice 28 :

a) Tracer trois points R, S et T non alignés.

Construire un point K à égale distance des trois points.

C’est le point d’intersection des médiatrices du triangle RST.

b) Comment s’appelle le point que tu as construit ? Y a-t-il plusieurs solutions ?

C’est le point d’intersection des médiatrices du triangle RST. Non, la solution est unique.

Exercice 29 :

a) Tracer un segment [AB] de longueur 3,8 cm.

Construire un triangle ABC sachant que côté [AC] mesure 5 cm et que le rayon du cercle circonscrit est de 3 cm.

b) Combien y a-t-il de triangles possibles ?

c) Construis-les tous.

Exercice 30 :

a) Construire les triangles EFG et MNP tels que :

· EF 8,4 cm, FG = 7,4 cm et EG = 6,3 cm ;

· MN 5,9 cm, NP = 6,5 cm et MP = 8 cm.

b) Tracer leur cercle circonscrit.

c) Quelle différence y-a-t-il entre les centres de ces deux cercles ?

Exercice 31 :

Construire à chaque fois le cercle circonscrit d’un triangle ABC :

a) AB 4,5 cm, BC 7 cm et 75°.

b) ABC est isocèle en A avec AB = 5 cm et 120°.

c) ABC est équilatéral ce côté 6 cm.

d) ABC est rectangle en A, avec AB = 5 cm et AC = 7 cm.

4.6/5 - (22443 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «triangle : corrigé des exercices de maths en 5ème en PDF.» au format PDF.