Signaler une erreur / Remarque ?
Sommaire de cette fiche
I. Introduction :
Il existe un nouvel ensemble de nombres : les nombres relatifs .Il y en a deux sortes :
- – Les nombres relatifs positifs :
; - – Les nombres relatifs négatifs : .
Ces nombres relatifs sont utilisés dans de nombreux cas :
- Frises chronologiques en histoire;
- Les températures ;
- Les découverts à la banque ;
- Les altitudes ( au-dessus ou en-dessous du niveau de la mer).
- le déplacement du lutin dans Scratch.
Remarque :
La calculatrice connaît les nombres relatifs ainsi que toutes les priorités opératoires
et elle sait également effectuer des calculs avec les nombres relatifs.
II.Repérage et droite graduée :
1. définition :
Les nombres relatifs regroupent les nombres positifs et les nombres négatifs.
Ils sont composés de deux éléments :
- leur signe;
- leur partie numérique (appelée également, sur une droite graduée, la distance à zéro)
Remarque :
La distance à zéro est la distance qui sépare un nombre relatif à zéro.
Exemples :
La distance à zéro de est .
La distance à zéro de est .
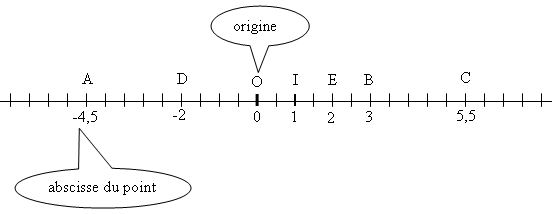
2. Repérage sur une droite graduée :
On peut utiliser les nombres relatifs pour repérer des points sur une droite graduée.
Il faut d’abord choisir un repère de deux points O et I auxquels on fait correspondre les nombres 0 et 1.
O s’appelle l’origine du repère.
La distance OI est l’unité du repère donc OI = 1.
A chaque point du repère on fait correspondre un nombre relatif appelé abscisse de ce point .
Exemple :
Le point A a pour abscisse
et se lit le point A d’abscisse
La distance à zéro du point A est .
Remarque :
Deux point A et B symétriques par rapport à l’origine O du repère de la droite graduée ont la même distance à zéro.
3. Nombres opposés :
L’opposé d’un nombre relatif est le nombre :
- qui a la même partie numérique ( ou distance à zéro);
- qui est de signe contraire.
Exemples :
est l’opposé du nombre relatif .
est l’opposé du nombre relatif .
Deux nombres opposés sont représentés par des points qui seront symétriques par rapport à l’origine sur une droite graduée.
III. Comparaison de nombres relatifs :
1. Nombres relatifs de signes différents :
Un nombre relatif négatif est toujours inférieur à un nombre relatif positif.
Exemples :
2. Nombres relatifs positifs :
Si deux nombres relatifs sont positifs alors le plus grand est celui qui a la plus grande partie numérique (ou distance à zéro).
Exemples :
3. Nombres relatifs négatifs :
Si deux nombres relatifs sont négatifs alors le plus grand est celui qui a la plus petite partie numérique (ou distance à zéro).
Exemples :
Addition et soustraction de nombres relatifs :
1. Addition de deux nombres relatifs :
La somme de deux nombres relatifs opposés est nulle.
Exemple :
Si les deux nombres relatifs ont le même signe alors la somme de ces deux nombres relatifs :
– a comme signe, le signe en commun;
– a pour partie numérique la somme des deux parties numériques .
Exemples :
Si les deux nombres relatifs sont de signe différents alors la somme est le nombre relatif :
– qui a le même signe que celui qui a la plus grande partie numérique;
– qui a pour partie numérique la différence de la plus grande partie numérique et de la plus petite.
Exemples :
2. Soustraction de deux nombres relatifs :
Soustraire un nombre relatif, c’est ajouter son opposé.
Exemples :
3. Calculs d’expressions numériques :
Afin de calculer des expressions numériques, il faut transformer les soustractions en additions,
puis appliquer les règles de calculs précédentes, en effectuant les calculs dans le sens de la lecture.
On ne note pas un signe + en début de ligne.
Exemples :
Calculer
Vous avez assimilé le cours sur les nombres relatifs en 5ème ?
Effectuez ce QCM de maths en cinquième sur les nombres relatifs afin d’évaluer vos acquis sur cette leçon.
Cette publication est également disponible en :
English (Anglais) 
Español (Espagnol) 
العربية (Arabe)
Télécharger et imprimer ce document en PDF gratuitement
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «nombres relatifs et repérage : cours de maths en 5ème» au format PDF.
D'autres fiches dans la section cours de maths en 5ème
- Le parallélogramme : cours de maths en 5ème
- Fractions : cours de maths en 5ème à télécharger en PDF.
- Les angles correspondants et alternes-internes : cours de maths en 5ème.
- Calcul littéral et simple distributivité : cours de maths en 5ème
- Nombres relatifs et repérage : cours de maths en 5ème
- Symétrie centrale et centre de symétrie : cours de maths en 5ème
- Priorités opératoires : cours de maths en 5ème
- Les statistiques : cours de maths en 5ème
- Proportionnalité : cours de maths en 5ème
- Les triangles et son cercle circonscrit et l’inégalité triangulaire : cours de maths en 5ème
D'autres fiches similaires à nombres relatifs et repérage : cours de maths en 5ème.
- 57
Des cours de maths en 5ème au programme de la classe de cinquième en ligne qui vous permettent de réviser et de revoir des points du cours que vous n'auriez pas compris.Ces leçons sont destinées aux professeurs mais également aux élèves désireux d'avoir une autre version de celle abordée en… - 56Le parallélogramme avec un cours de maths en 5ème où nous traiterons de la définition, des propriétés ainsi que des parallélogrammes particuliers comme le rectangle, le losange et le carré ainsi que la construction à la règle et compas en classe de cinquième au cycle 4. I. Définition et vocabulaire : 1. Rappels : Définition et vocabulaire…
- 56La proportionnalité dans un cours de maths en 5ème où nous étudierons les grandeurs proportionnelles ainsi que des tableaux de proportionnalité ainsi que les différentes propriétés et la détermination du coefficient de proportionnalité. la règle du produit en croix et la calcul de la quatrième proportionnelle. Nous terminerons cette leçon…
Les dernières fiches mises à jour.
Voici les dernières ressources similaires à nombres relatifs et repérage : cours de maths en 5ème mis à jour sur Mathovore (des cours, exercices, des contrôles et autres), rédigées par notre équipe d'enseignants.
