Priorités et calculs : exercices de maths en 5ème corrigés en PDF.

Mis à jour le 28 mai 2025

Sommaire

✏️Exercices

5ème • Collège

Priorités et calculs

⏱️ Temps de travail : 20-45 min

🎯 Niveau : Collège

📱 Format : Gratuit

📄 PDF : Disponible

Les opérations et priorités opératoires à travers des exercices de maths en 5ème corrigés. Cette fiche est à imprimer en PDF.

Exercice 1 – Calculer les expressions.

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

a) $7\,+\,4\,\times \,8$ b) $3\,\times \,11\,-\,7\,\times \,4$ c) $37-6\,\times \,5$

d) $9\,-4\,:\,4$ e) $32\,:\,4-2\,+\,7\,\times \,3$ f) $9\,\times \,4\,:\,2\,-\,5\,\times \,2$

Exercice 2 – effectuer les calculs.

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

$A\,=6\,\times \,(3\,+\,7)$ $B\,=23\,-\,4\,\times \,5$ $C\,=(3\,+\,5)\,\times \,(9\,-\,7)$

$D\,=(13\,-\,7)\,:\,2$ $E\,=5\,-\,[4\,-\,(2\,+\,1)]$ $F\,=(3\,+\,5\,\times \,7)\,:\,2\,+1$

Exercice 3 – Problème du pot de confiture.

Aurélie achète 5 pots de confitures à 9 € pièce et 12 baguettes à 6,50 € pièce.

Écris un calcul te permettant de trouver le prix total qu’elle doit payer.

Exercice 4 – placer des parenthèses.

Recopie sur ta feuille les expressions suivantes en ajoutant des parenthèses pour que l’égalité soit vraie :

$8\,+\,2\,\times \,5\,=50$ ; $9\,-\,3\,\times \,2\,+\,5\,=42$ ; $8\,+\,4\,\times \,3\,:\,2\,=18$

Exercice 5 – expressions et calculs.

Calcule les expressions suivantes :

$A=24-\,5\,-1$ $B\,=14\,\times \,3\,-\,5\,\times \,2$ $C\,=10\,:\,[\,6\,-2\,\times \,(1\,-0,5)\,]\,\times \,5$

$D\,=8\,:\,4\,-\,0,25\,\times \,2$ $E\,=3\,\times \,(7\,-\,2)\,-\,4$ $F\,=72\,:\,9\,\times \,8\,:\,2\,-\,9\,\times \,3$

Exercice 6 – obtenir des résultats.

En utilisant une seule fois les nombres 3 ; 7 ; 10 et

autant de fois que tu veux les signes + − x : ( ) essaie d’obtenir les résultats suivants :

20 ; 14 ; 31 ; 67 ; 40 ; 1.

Exercice 7 – Placer des parenthèses.

Mets les parenthèses et les crochets pour que l’égalité soit vraie :

$5\,\times \,4\,-\,1\,+\,2\,\times \,2\,=\,34$

Exercice 8 – Problème de football.

L’entraîneur d’une équipe de football doit acheter 16 équipements pour ses joueurs.

Chaque équipement est composé d’un maillot à 24€, d’un short à 11€ et d’une paire de chaussettes à 4,50€.

Écrire l’expression permettant de calculer le montant de ses achats.

Exercice 9 – Problème du boxeur.

Un boxeur pèse 86,2 kg à une semaine d’un combat.

Il fait un régime qui lui permet de perdre 0,6 kg pendant 7 jours.

Écrire l’expression qui permet de calculer le poids du boxeur le jour du combat.

Exercice 10 – calculer des expressions.

Calculer les expressions suivantes:

A = 125 − 7 x4 + 11 B = (125 − 7) x4 + 11 C = 125 − 7 x(4 + 11)

D = 125 − (7 x4) + 11 E = [(125 − 7) x4] + 11 F = 125 − [7 x(4 + 11)]

Exercice 11 – Priorités des opérations.

Calcule en respectant les priorités:

1) 12,7 + 3,1×2 2) 12,7 – 3,1×2 3) 12,7 x3 + 3,1×7

4) 12,7 x3 − 3,1×8 5) (5 − 3) x(9,1 − 7,8) 6) (5 + 3) x(9,1 + 7,8)

Exercice 12 – Calculs et étapes intermédiaires.

En écrivant les étapes intermédiaires, calculer les expressions suivantes :

A = = − 4 + 15 + ( 9 – 4) – 2 + (−4 + 1 )

B = − 35 + [12 + ( 75 − 55) − (15 − 8 ) ] + 7

C = 4 − (7 – 3 ) − [ 11 − ( 8 − 5)]

Exercice 13 – Des égalités exactes ou fausses.

Pour chaque égalité, indique si elle est exacte ou corrige en plaçant les parenthèses indispensables.

a) 6 + 5 x5 – 3 =28 b) 6 + 5 x5 – 3 =52

c) 6 + 5 x5 – 3 =16 d) 6 + 5 x5 – 3 =22

Exercice 14 – Priorités des opérations.

Calcule en indiquant les étapes intermédiaires :

A = 25 − 7 x(8 − 5) B = (7 − 4) x3 + 4 − (7 x2 − 8)

C = 8 x3 − (12 : 3 + 2) x3 D = [10 + 5 x(6 – 4)] : 4

Exercice 15 – Calculer des expressions
Calculer les expressions suivantes en écrivant les étapes intermédiaires:

A = 7 + 4 x8 B = 3 x11– 7×4 C = 37 – 6 x5

D = 9 – 4 : 4 E = 32 ÷ 4 – 2 + 7 ´3 F = 9 x 4:2 – 5 x2

Exercice 16 – Calculs numériques

Calculer les expressions suivantes en écrivant les étapes intermédiaires:

x = 132 – 11×10 + 4 x2,5 y = 12,5 – 2 – 5,1 + 15 – 1,2

z = 120 – 4×5 – 7x´8 + 54 : 9 t = 22 + 3×1,5 – 1,5

Exercice 17 – Ranger dans l’ordre croissant

Calculer et ranger les cinq résultats ci-dessous par ordre croissant :

X = 2,9 + 0,8 x5 T = 4 x0,5 + 3 x1,36 C = 12,8 – 0,7 x 9

A = 10 – 9,9 : 3 E = 0,23 x 5 + 99,18 :17,1

Exercice 18 – Calculer des expressions numériques

Calculer les expressions suivantes en écrivant les étapes intermédiaires:

M = (6 + 2) x 7 N = 17 x (15 – 11) O = (3,5 + 6,5)x(14 – 9,5) P = (18 – 11) x(5 + 9)

Exercice 19 – Des expressions à calculer

Calculer les expressions suivantes :

A =6 x (3 + 7) B =23 – 4 x 5 C =(3 + 5)x (9 – 7)

D =(13 – 7) : 2 E =5 – [4 – (2 + 1)] F =(3 + 5x 7) : 2 +1

Exercice 20 – Relier expression et résultat

Relier par une flèche chaque calcul à son résultat :

(5 + 5) x(5 + 5) . . 6

5 x(5 + 5 + 5) . . 10

5 + (5 + 5) x5 . . 55

(5 + 5) x(5 : 5) . . 75

(5 + (5 x5)) :5 . . 100

Exercice 21 – Ecrire une expression numérique

En utilisant une seule fois les nombres 3 ; 7 ; 10 et autant de fois que tu veux les signes + – : et ( ) essayer d’obtenir les résultats suivants : 20 ; 14 ; 31 ; 67 ; 40 ; 1.

Exercice 22 – Placer correctement des parenthèses

Mettre les parenthèses et les crochets pour que l’égalité soit vraie :

5 x4 – 1 + 2×2 = 34

Exercice 23 – Calculs avec des parenthèses.

Effectuer les calculs suivants en détaillant les différentes étapes :

$A=8\times (26-14)$

$C=(0,5+15+35+8,5+1,75)\times (55+45))$
$D=(1,2+3,8)\times (5,5-4)-(7,5-6)$

Exercice 24 – Calculs avec des parenthèses imbriquées.

Calculer les expressions en détaillant les calculs :

$A=7\times [16-(2+9)]$
$B=[9-(9-8)]\times [(2+7):3]$
$C=4\times [39,2-(2,4+4,8)+3]$

Exercice 25 – Retrouvez les calculs.

Traduire par une expression numérique :

a. La somme de 7,5 et du produit de 3 par 1,5 ;
b. Le produit de 7,5 par la somme de 3 et 1,5 ;
c. Le quotient de la somme de 12 et 8 par 100 ;
d. La somme du produit de 3 par 6 et du résultat de la soustraction de 7 à 15.

Exercice 26 – Enchaînement d’opérations.

Calculer les expressions numériques suivantes :

$A = 12 + 8 \times 5 - 4 + 16 : 2 \\B = 17 -(3 + 8 - 5) \\C = 18 + 4 \times (7 \times 2 - 6) \\D = 75 - (6 + 3 \times 10) : 9 \\E = 3 200 \times 0,01 \times 100 - 100 \\F = (5,6 + 1,4) \times (3,4 - 1,4) \\G = 48 + 2 \times (7 + 3 \times 5 - 2 \times 10) \\H = 5 + 3 \times 6 - 8 : 2 \\I = 24,1 - [9 - (2 + 5)] \\J = 15,1 - [17 - (30- 20)] \\K = 128 - 4 \times (6 + 1) + 218 - 3 \times (7 - 1)$

Exercice 27 – Calcul numérique et parenthèses.

Calculer les expression numériques suivantes :

$A\,=\,12\,+\,[3\,\times \,[5\,+\,(4\,\times \,7)\,+\,2]]\,+\,(8\,\times \,3)$

$B\,=\,25\,-\,[12\,-\,(3\,+\,4)]$

$C\,=\,81\,+\,[(7\,+\,21)\,-\,13]\,-\,(17\,-\,9)$

$D\,=\,[(7,8\,-\,4,5)\,+\,11]\times \,(4\,+\,3)$

$E\,=\,6\,+\,[(7\,\times \,2)\,-\,(1,1\,\times \,2)]$

Exercice 28 – Problème du libraire.

Un libraire a reçu un premier colis contenant 50 tomes d’Harry Potter, puis un second en contenant 80.

Il les range sur des étagères qui peuvent contenir 13 livres.

Combien d’étagères remplira-t-il ?

Exercice 29 – Brocante et prix d’un DVD.

Lors d’une brocante, Marc a acheté 8 livres, 4 dvd et 2 bd.

Chaque livre coutait 1.5 euro et une bd 4 euros.

Il a paye en tout 38 euros .

Quel est le prix d’un DVD ?

Exercice 30 – Priorités opératoires.

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

a) 7 + 4x 8

b) 3×11 − 7x 4

c) 37 − 6x 5

d) 9 − 4 : 4

e) 32 ÷ 4 − 2 + 7 x 3

f) 9 x4 : 2 − 5x 2

Exercice 31 – Problème et expression numérique.

Associe à chaque problème la bonne expression. Calcule ensuite en détaillant les
calculs :
1) Un éleveur possède 102 œufs et en ramasse 18 autres. Il doit expédier ses œufs par boîte de 12. Combien expédiera-t-il de boîtes ?

2) L’intendance du collège achète 102 cartons de papier blanc et 12 de papier de couleur. Un carton coûte 18 €.

Quel est le prix total à payer ?

3) Un grand magasin reçoit sa livraison de jus de fruit, soit 18 cartons de 12 bouteilles. Il reste en réserve 102

bouteilles. Combien y a-t-il maintenant de bouteilles de jus de fruit dans ce grand magasin ?

Exercice 32 – Problème du libraire et opérations.

Un libraire a reçu un premier colis contenant 50 tomes d’Harry Potter,

puis un second en contenant 80.
Il les range sur des étagères qui peuvent contenir 13 livres.
Combien d’étagères remplira-til ?

Exercice 33 – Priorités et calcul numérique.

Calculer les expressions numériques suivantes:

$A = 15 + 60 : 5 \times 6 - 3 ; \\ B = 45 \times 8 - 20 : 4 \times 2 ; \\ C = 150 - (45 - 8 - 3)- 34 ;\\ D = 25 : (12 -4 -3) : 5 ;\\ E = 48 + 36 : 6 : 3 ;\\ M = 40 : 4 \times 5 ; \\ N = 24 : 6 \times 2 ;\\ O = 15 - 7 - 6 + 1.$

Exercice 34 – Placer correctement des parenthèses.

Recopier les expressions suivantes en plaçant des parenthèses pour obtenir les résultats donnés :

$9 + 3\times 15 = 180 ;\\ 2 + 3 \times 5 + 4 = 45 ;\\ 8 + 9\times 6 + 4 = 106 ; \\ 9 \times 5 + 17 = 198 ;\\ 1 + 2 \times 3 = 9 ; \\ 2 \times 3 + 5 \times 8 + 2 = 106 ;\\ 7 \times 2 + 6 = 56 ; \\ 3\times 5 + 1 - 10 = 8$

Exercice 35 – Expressions contenant des parenthèses.

Calculer les expressions numériques suivantes :

A =(5 + 7)x 2 ; B= 5 + 7x 2 ; C= (12 – 4)x 3 ; D= 12 – 4 x 3 ; E= (21 – 18)x (12 – 10) + 1.

F= 18 + [12 – 2x (13 – 9)] ; G= (4,8 – (2,5 + 0,3))x (3 + 3,5) ; H =[18 + 2 x(120 – 45)] x1,5 ;

I =700 – [300 – (300 – 80)].

Exercice 36 – Enchaînement de calculs.

Calculer les expressions numériques suivantes en respectant les priorités opératoires.

$A= 6 + 27 : 3 \\ B = 24 : 3 + 16 : 8 - 2 \\ C = 8\times 6 -23 \\ D = 5\times 6 + 4 \times 3\\ E = 7 + 15 : 3 \times 5 \\ F = 3 + 4 \times 5 - 1 \\ G = 15\times 5 - 2 \\ H = 55 - 7 \times 6 + 1\\ I = 12 \times 4 - 15 :3.$

Exercice 37 – Problème des bd.

Au stand d’un vide grenier, Pierre s’est acheté 4 BD de Titeuf à 2,50 € chacune et une voiture télécommandé pour 6 €. Il a payé avec un billet de 20 €.

Écris en une seule expression le calcul donnant la monnaie rendue, puis effectue le calcul.

Exercice 38 – Problème sur le bidon d’huile.

J’ai acheté un bidon d’huile à 12 € et quatre pneus à 45 € l’un.

Écris en une seule expression le calcul donnant le montant de la dépense.

Effectue ensuite ce calcul.

Exercice 39 – Traduis chaque phrase par un calcul.

· F est le produit de 4 par la somme de 12 et de 5.

· G est la somme du produit de 6 par 8 et de 20.

· H est la somme de 9 et du produit de 11 par 3.

· I est le quotient de la somme de 8 et 4 par 6.

· J est la différence de 7 et du quotient de 25 par 7.

· K est le quotient de 9 par la différence de 7 et 4.

· L est le produit de la différence de 15 et 7 par 8.

· M est la somme du produit de 8 par 4 et du produit de 7 par 3.

· N est le produit de la somme de 15 et 7 par la différence de 17 et 5.

Exercice 40

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

a) 7 + 4 $\times$ 8 b) 3 $\times$ 11 − 7 $\times$ 4 c) 37 − 6 $\times$ 5 d) 9 − 4 : 4 e) 32 ÷ 4 − 2 + 7 $\times$ 3 f) 9 $\times$ 4 : 2 − 5 $\times$ 2

Exercice 41

Calculer les expressions suivantes en écrivant les étapes intermédiaires :

A = 6 $\times$ (3 + 7) B = 23 − 4 $\times$ 5 C = (3 + 5) $\times$ (9 − 7) D = (13 − 7) : 2 E = 5 − [4 − (2 + 1)] F = (3 + 5 $\times$ 7) : 2 +1

Exercice 42

Aurélie achète 5 pots de confitures à 1,50 € pièce et 12 baguettes à 0,95 € pièce.

Écrire un calcul te permettant de trouver le prix total qu’elle doit payer.

Exercice 43

Recopier sur ta feuille les expressions suivantes en ajoutant des parenthèses pour que l’égalité soit vraie :

8 + 2 $\times$ 5 = 50 ; 9 − 3 $\times$ 2 + 5 = 42 ; 8 + 4 $\times$ 3 : 2 = 18

Exercice 44

Calculer les expressions suivantes :

A = 24 − 5 − 1

B =14 $\times$ 3 − 5 $\times$ 2

C = 10 : [ 6 − 2 $\times$ (1 − 0,5) ] $\times$ 5

D = 8 : 4 − 0,25 $\times$ 2

E= 3 $\times$ (7 − 2) − 4

F = 72 : 9 $\times$ 8 : 2 − 9 $\times$ 3

Exercice 45

En utilisant autant de fois les nombres 3 ; 7 ; 10 et autant de fois que tu veux les signes + − $\times$ : ( ) essaie d’obtenir les résultats suivants :

20 ; 14 ; 31 ; 67 ; 40 ; 1.

Exercice 46

Mets les parenthèses et les crochets pour que l’égalité soit vraie :

5 $\times$ 4 − 1 + 2 $\times$ 2 = 34

Exercice 47

L’entraîneur d’une équipe de football doit acheter 16 équipements pour ses joueurs.

Chaque équipement est composé d’un maillot à 24€, d’un short à 11€ et d’une paire de chaussettes à 4,50€.

Écrire l’expression permettant de calculer le montant de ses achats.

Exercice 48

Un boxeur pèse 86,2 kg à une semaine d’un combat.

Il fait un régime qui lui permet de perdre 0,6 kg pendant 7 jours.

Écrire l’expression qui permet de calculer le poids du boxeur le jour du combat.

Exercice 49

Calculer les expressions suivantes:

A = 125 − 7 $\times$ 4 + 11

B = (125 − 7) $\times$ 4 + 11

C = 125 − 7 $\times$ (4 + 11)

D = 125 − (7 $\times$ 4) + 11

E = [(125 − 7) $\times$ 4] + 11

F = 125 − [7 $\times$ (4 + 11)]

Exercice 50

Calculer en respectant les priorités:

1) 12,7 + 3,1 $\times$ 2

2) 12,7 – 3,1 $\times$ 2

3) 12,7 $\times$ 3 + 3,1 $\times$ 7

4) 12,7 $\times$ 3 − 3,1 $\times$ 8

5) (5 − 3) $\times$ (9,1 − 7,8)

6) (5 + 3) $\times$ (9,1 + 7,8)

Exercice 51

En écrivant les étapes intermédiaires, calculer les expressions suivantes :

A = − 4 + 15 + ( 9 – 4) – 2 + (−4 + 1 )

B = − 35 + [12 + ( 75 − 55) − (15 − 8 ) ] + 7

C = 4 − (7 – 3 ) − [ 11 − ( 8 − 5)]

Exercice 52

Pour chaque égalité, indiquer si elle est exacte ou corriger en plaçant les parenthèses indispensables.

a) 6 + 5 $\times$ 5 – 3 = 28 b) 6 + 5 $\times$ 5 – 3 = 52

c) 6 + 5 $\times$ 5 – 3 = 16 d) 6 + 5 $\times$ 5 – 3 = 22

Exercice 53

Calculer en indiquant les étapes intermédiaires :

A = 25 − 7 $\times$ (8 − 5) B = (7 − 4) $\times$ 3 + 4 − (7 $\times$ 2 − 8)

C = 8 $\times$ 3 − (12 : 3 + 2) $\times$ 3 D = [10 + 5 $\times$ (6 – 4)] : 4

Exercice 54

Relier par une flèche chaque calcul à son résultat :

(5 + 5) $\times$ (5 + 5) · · 6

5 $\times$ (5 + 5 + 5) ) · · 10

5 + ((5 + 5) $\times$ 5) · · 55

(5 + 5) $\times$ (5 : 5) · · 75

(5 + (5 $\times$ 5)) : 5 · · 100

Exercice 55

Au rayon lait d’un supermarché, il y a au début de la journée 52 packs de 6 bouteilles de lait chacun.

Dans la journée, il s’est vendu 18 packs entiers et 63 bouteilles à l’unité.

1) Écrire une expression avec parenthèses permettant de calculer le nombre de bouteilles restant dans le rayon à la fin de la journée.

2) Écrire aussi une expression sans parenthèse.

3) Faire le calcul.

Exercice 56

On donne l’expression littérale E = 2x + y (3y − x ) − 5

1) Calculer E lorsque x = 2 et y = 3

2) Calculer E lorsque x = 3,5 et y = 1

3) Calculer E lorsque x = 3 et y = 2

Exercice 57

Effectuer les calculs suivant en soulignant le calcul en cours.

A=24+3×7 B=720 : 9+4

C=60-14+5×3+2 D=8×3-5×4×0,2

E=15 :5-2

Exercice 58

Effectuer les calculs suivant en soulignant le calcul en cours.

A=25-(8-3)+1 B=25-(8-3+1)

C=18-[4×(5-3)+2] D=[2+0,1×(5+3)] :4 E=24 :[8-(3+1))]

Exercice 59

Placer les parenthèses pour que les égalités suivantes soient vraies et vérifier chacune de vos réponses.

a) 4×2+9=44 b) 1+13-14-7=7 c) 15-3×2=24

d) 2×5-2×4+1=30 e) 32 – 4+7×2=10 f) 7+7+6×7=98

Exercice 60

Associer chaque expression à une phrase :

7×(4+3) · · La différence du produit de 4 par 3 et de 7

7×4+3 · · Le produit de 7 par la somme de 4 et de 3

4×3-7 · · Le produit de la différence de 7 et 4 par 3

(7-4) ×3 · · La somme du produit de 7 par 4 et de 3

Exercice 61

Traduis chaque phrase par une expression mathématique .

a) A est la somme du produit de 5 par 2 et de 3 alors A=……

b) B est le produit de 4 par la somme de 9 et de 7 alors B=…..

c) C est la différence de 17 et du produit de 4 par 3 alors C=…..

d) D est le quotient de la somme de 19 et 3 par 11 alors D=….

Exercice 62

Calculer les expressions suivantes sur votre cahier.

A=35-[4× (5+2)-7]

B=12×[32-(4+7) ×2]

C=(1+7) ×[11-(2+3)]

D=12+[(120-20)-2×4×5]

E=150-10-[(12+2) ×4+2]

F=(60-59,9) ×[30-(25-15)]

Exercice 63

I) Calculer :

$A = 12 + 8 \times 5 - 4 + 16 : 2$

$C = 18 + 4 \times (7 \times 2 - 6)$

$D = 75 - (6 + 3 \times 10) : 9$

$E = 3 200 \times 0,01 \times 100-100$

$F = (5,6 + 1,4) \times (3,4- 1,4)$

$G = 48 + 2 \times (7 + 3 \times 5 - 2 \times 10)$

$H = 5 + 3 \times 6 - 8 : 2$

$K = 128 - 4 \times (6 + 1) + 218 - 3 \times (7 - 1)$

$L = 8 + 2 \times (15 - 5 \times 2 + 4)$

$M = 8 \times [9 - (2 + 4)] - 5 + 2$

$N = 6 + 4 \times [2 \times (11 - 4 \times 2 + 2) - (9 - 5)]$

O = 17 − [3 × (5 − 2) + 8] + 12,3 × 4 − 4

$P = 3,5 \times [12 - (7 + 3)]$

Q = 2,5 × [3 + 2 × (13 − 3 × 3) − 6 − 3]

R = 38 − 8 × (7 − 2 × 3 + 1) − 4 + 2

S = 6 + 2 × 8 – 5 × 3 + 10 : 2

T = [(6 + 2) × (8 – 5) × 3 + 10] : 2

U = 6 + [2 × (8 – 5) × 3 + 10 : 2]

V = (19 – 7) × 4 – (28 – 14)

W = 25 – [18,7 – (9,2 + 4,5)]

X = [35 – (17 – 6)] : 8

Y = 2 × [(25 – 17,1) × 3 + 11,3]

Z = [35 – 56 : (28 – 20)] × 10

II) Calculer astucieusement :

$B = 8 \times 8765,43 \times 4 \times 0,125 \times 2,5$

$D =0,4 \times 56,49 \times 12,5 \times 25 \times 0,08$

$F = 17,3 + 12 \times 2 + 1,4 + 2,7 + 2,3 \times 2$

$G = 2 - 1,2 + 0,71 + 1,1 \times 2 + 12 + 0,29$

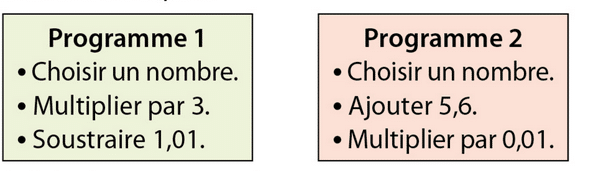
Exercice 64

a. Pour chacun des programmes de calcul ci-dessous, écrire une expression qui permet de
calculer le nombre obtenu lorsqu’on choisit 0,7 comme nombre de départ.

b. Calculer ces expressions.

Exercice 65

a. Laquelle de ces expressions correspond à la description de Sofiane ?
$C=(5,29 \times 10+78) \times 001 \,\,D=5,29 \times (10+ 78) \times 0,01 \\E=5,29 \times 10+78 \times 0,01\,\, F=5,29 \times (10+78 \times 0,01)$
b. Calculer cette expression.

Exercice 66

Associer l’une des expressions À, B, C ou D à chacun des trois problèmes, puis donner les
réponses aux problèmes.
$A=5 \times (4+8) \,\,B=4+5 \times 8 \\C=5+4 \times 8 \,\, D=5 \times 4+5 \times 8$

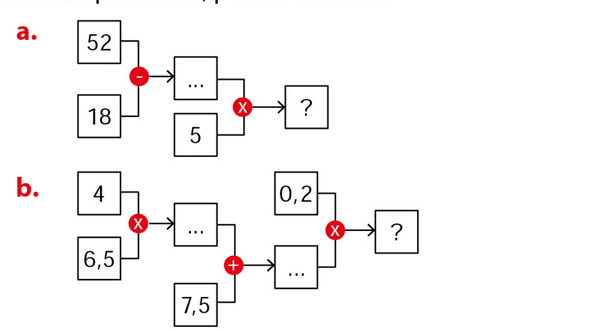
Exercice 67

Calculer à la main chaque expression.
$A=21,4-(24-7):2 \\B=(13-4) \times 0,6-3,8 \\C= 34,5 - 30 \times (1 - 0,6) \\D=(16+2):5-2$

Exercice 68

Écrire l’expression qui correspond à la succession d’opérations, puis la calculer.

Exercice 69

Voici les achats que Clara veut effectuer avec un billet de 50€.

1. Expliquer à l’aide d’ordres de grandeur pourquoi le billet de 50 € suffira.
2. a. Écrire l’expression R qui permet de calculer la somme que l’on rendra à Clara.
b. Calculer R.

4.2/5 - (23020 votes)

×12

L’équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «priorités et calculs : exercices de maths en 5ème corrigés en PDF.» au format PDF.