Volumes : exercices de maths en 5ème corrigés en PDF.
Mis à jour le 17 décembre 2025
Exercice 1 – Longueur et aire d’un petit suisse.
1°) Calculer la longueur du papier entourant le petit suisse, sachant qu’il y a un recouvrement de 5 mm.
( Réponse arrondie à 1 mm.)
2°) Calculer l’aire du papier.

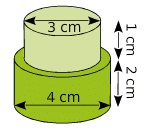
Exercice 2 – Volume d’une pièce montée.
Calculer le volume de la pièce montée sachant
que chaque couche est cylindrique et mesure 6 cm de haut.
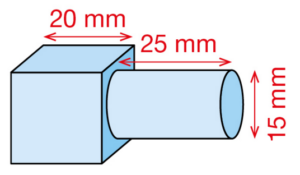
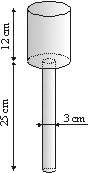
Exercice 3 – Calculer le volume d’un outil de carrossier.
Un outil de carrossier est constitué de deux cylindres comme le montre la figure ci-contre.
Le rayon du cylindre du dessus vaut le double de celui du dessous.
Calculer son volume (arrondir au cm3).
Exercice 4 – Calcul du volume d’une boîte de chocolat.
a) Calculer le volume de cette boîte de chocolat en poudre.
b) Calculer le volume de poudre gratuit offert en promotion.

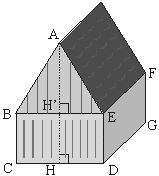
Exercice 5 – Volume d’un hangar.
La figure ci-contre représente un hangar qui a la forme d’un pavé droit surmonté d’un prisme droit à base triangulaire.
La hauteur AH de la façade est égale à 12,5 m.
CD = 9 m ; ED = 5,2 m ; GD = 16 m.
a) Calcule la hauteur AH’ du triangle isocèle ABE.
b) Calcule l’aire du polygone ABCDE.
c) Déduis-en le volume du hangar.
Exercice 6 – Volume d’un flacon de parfum.
Ce flacon de parfum a la forme d’un prisme droit de hauteur 12 cm.
Ses bases sont des octogones réguliers, dont les dimensions sont indiquées sur le dessin de droite.
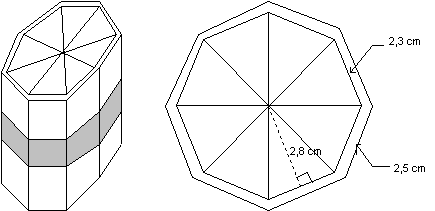
a) Calculer l’aire de la base (en blanc sur le dessin de droite ), puis calculer le volume intérieur du flacon en .
b) Pour signaler une promotion sur ce parfum,
chaque flacon est entouré d’une étiquette de 3,5 cm de haut.
Calculer l’aire de l’une de ces étiquettes.
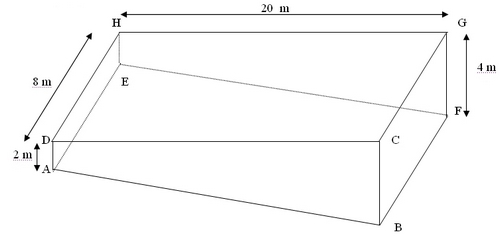
Exercice 7 – Etude d’une piscine
Le modèle mathématique d’une piscine est le prisme droit schématisé ci-dessous.
1.Par quelles lettres désigne-t-on les bases de ce prisme ?
2.Quelle est la nature géométrique des bases de ce prisme ?
3. Quelles sont les dimensions d’une base ?
4. Quelle est l’aire de la base ?
5. Quelle est l’aire de ce prisme ?
6. Par quelles lettres désigne-t-on les 4 faces latérales de ce prisme ?
7. Quelle est la hauteur de ce prisme ?
8. En déduire le volume de ce prisme ?
9. On remplit le volume de ce prisme au quatre cinquième d’eau.
Calculer en litres le volume d’eau.
Exercice 8 – Calcul du volume d’un prisme.
Le prisme droit ci-contre a une hauteur AA’ de 5 cm
et sa base est un quadrilatère ABCD d’aire .
Calculer son volume V.
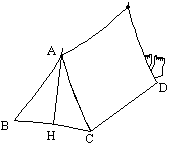
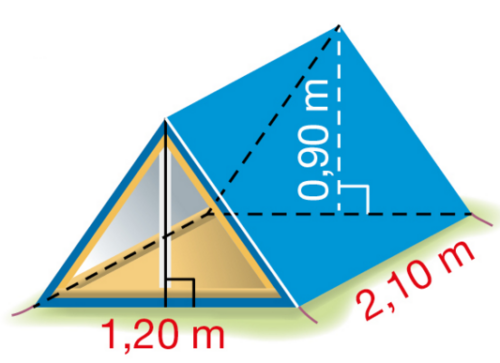
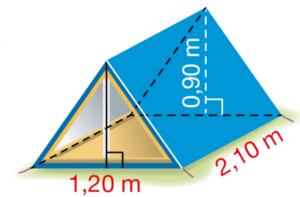
Exercice 9 – Calcul du volume d’une tente.
Une tente a la forme d’un prisme droit. Elle a une hauteur de AH de 2 m
et une longueur CD de 4,5 m. La face avant est un triangle isocèle de base BC= 1,5 m.
Calculer le volume de cette tente.
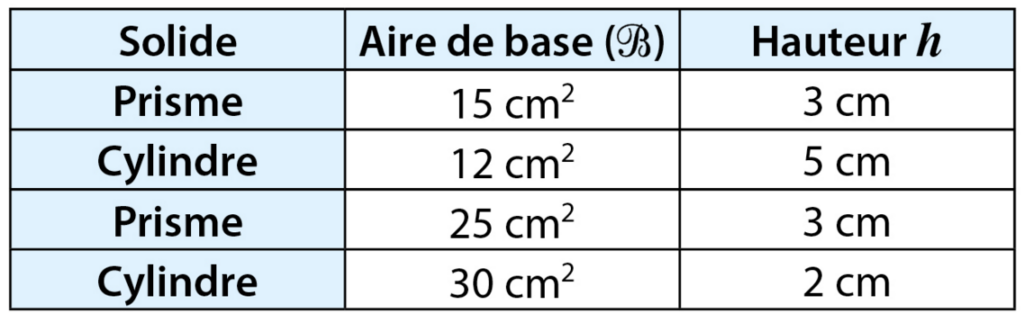
Exercice 10 – Convertir des volumes.
Complète :
1 m3 = ……dm 3 = … cm 3 = …mm 3
0,087 m 3 = … dm 3 = … cm 3 = … mm 3
345 000 mm 3 =…. cm 3 = … dm 3 = …… m 3
2. Exprimer en m 3 :
3 500 dm 3 ; 75 000 cm 3 ; 0,05 dm 3
2 450 mm 3 ; 8 510 dm 3 ; 470 dm 3
98,5 dm 3 ; 7,2 dm 3 ; 52 000 cm 3
6 900 cm 3 ; 527 cm 3 ; 648 000 000 mm 3
3. Convertir en dm 3 :
0,375 m 3 ; 38 m 3 ; 0,000 4 m 3
2 915 cm 3 ; 740 cm 3 ; 8,5 cm 3
34 000 mm 3 ; 7,5 mm 3 ; 28 mm 3
4. Convertir en cm 3 :
0,37 dm 3 ; 0,005 m 3 ; 47 mm 3
Exercice 11 – Perspective cavalière d’un prisme droit.
Voici en perspective cavalière la représentation d’un toit en forme de prisme droit.
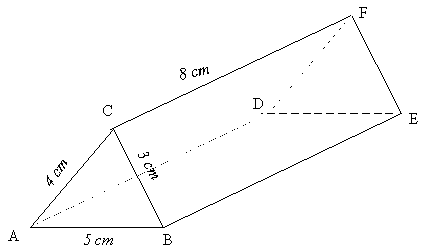
Combien mesure la hauteur de ce prisme droit ?
Nomme les bases ?
Nomme les faces latérales ?
Combien mesure la longueur DF ?
Combien mesure la longueur BE ?
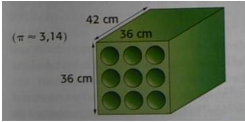
Exercice 12 – Volume d’un casier à bouteilles.
Un casier à bouteilles en plastique a la forme d’un pavé droit
contenant neuf compartiments cylindriques, de diamètre 10 cm chacun,
traversant le pavé dans toute sa profondeur.
1. Calculer le volume du pavé droit à partir duquel a été formé le casier.
2. Calculer le volume intérieur d’un compartiment.
3. En déduire le volume de plastique.
Exercice 13 – Calculer le volume d’une pièce.
Empilées, les cinq pièces d’un jeu de construction forment un mur
de 9cm de longueur, de 4 cm de hauteur et de 2 cm d’épaisseur.
Calculer le volume de ce mur .
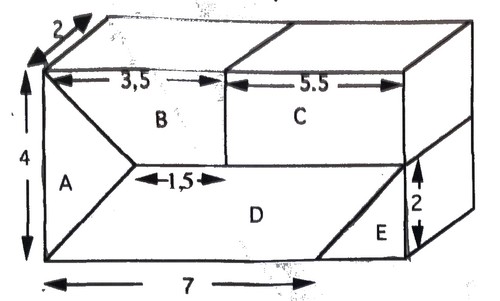
Exercice 14 :
Calculer le volume de chaque parallélépipède rectangle.
Exercice 15 :
Une plaquette de beurre a pour longueur 11,5 cm, pour largeur 6,5 cm et pour hauteur
4 cm. On la coupe en deux moitiés comme ci-dessus.
Calculer de deux façons différentes le volume de chacun des morceaux.
Exercice 16 :
Cette tente a la forme d’un prisme droit.
a. Calculer son volume.
b. Donner sa contenance en litres.
Exercice 17 :
Un gâteau cuit dans un moule cylindrique de diamètre 22 cm et de hauteur 6 cm.
Ce gâteau est partagé équitablement en 7 parts.
Calculer une valeur approchée au dixième près du volume, en , de chaque part.

Exercice 18 :
Une bougie a la forme d’un cône de révolution de hauteur 9 cm.
Le diamètre de la base est 5 cm.
Calculer une valeur approchée au dixième près du volume, en , de cette bougie.

Exercice 19 :
Dans le film Jurassic World, un véhicule a la forme d’une boule de 2 m de diamètre.
Calculer une valeur approchée au dixième près du volume, en , de cette boule.
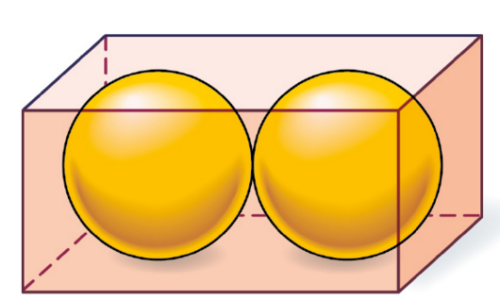
Exercice 20 :
Un parallélépipède rectangle de dimensions 4 cm, 4 cm et 8 cm contient deux boules de rayon 2 cm.
Calculer une valeur approchée au millième près du volume, en , de l’espace
laissé libre par les deux boules.
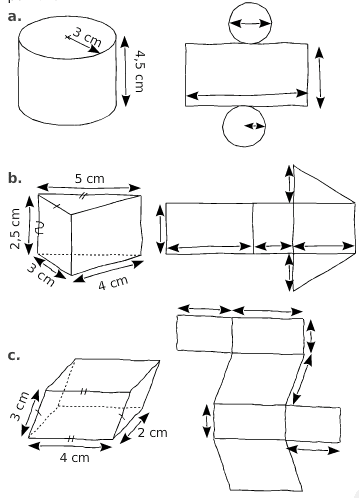
Exercice 21:
A l’aide des représentations en perspective cavalière, indiquer les longueurs
que vous connaissez et codez les segments de même longueur sur les patrons.
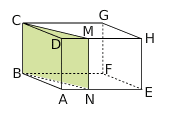
Exercice 22 :
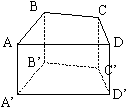
La figure ci-dessous représente le pavé droit ABCDEFGH, et sa section BCMN.
On donne AB = 5 cm; BC = 4 cm; AE = 6 cm.
- Quelle est la nature du quadrilatère BCMN ?
- Quelle est la nature du triangle CDM ?Combien vaut CD?
- Sachant que MD vaut 2 cm, représenter le triangle CDM, en vraie grandeur.
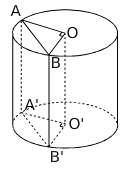
Exercice 23 :
On réalise la section ABB’A’ par un plan parallèle à l’axe d’un cylindre
de hauteur [OO’] mesurant 5 cm, et de rayon [OA] mesurant 3 cm, de sorte
que le triangle AOB soit rectangle en O.
1.Préciser la nature du triangle AOB.
2.Quelle est la nature de la section ABB’A’ ?
3.Représenter AOB et ABB’A’ en vraie grandeur.
Exercice 24 :
Effectuer les conversions suivantes :
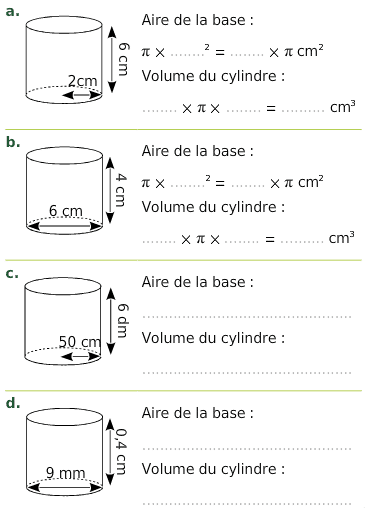
Exercice 25 :
Compléter les calculs pour déterminer le volume exact de chaque cylindre de révolution.
Exercice 26 :
Calculer le volume de la pièce métallique suivante (donner le résultat arrondi au près).
Exercice 27 :
Ce solide est composé d’un cube et d’un cylindre de révolution.
Calculer une valeur approchée à l’unité prés du volume, en , de ce solide.
Exercice 28 :
Un silo à grains est formé d’un cylindre de révolution de rayon 4,8 m et
de hauteur 12 m surmonté d’un cône de révolution de même rayon et de hauteur 2,4 m.
Calculer une valeur approchée à l’unité prés du volume, en , de ce silo.

Exercice 29 :
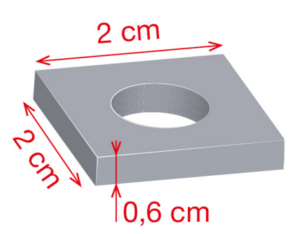
Un écrou est constitué d’un parallélépipède rectangle auquel on a enlevé un
cylindre de diamètre 1 cm.
Calculer une valeur approchée au dixième prés du volume, en , de cet écrou.
Exercice 30 :
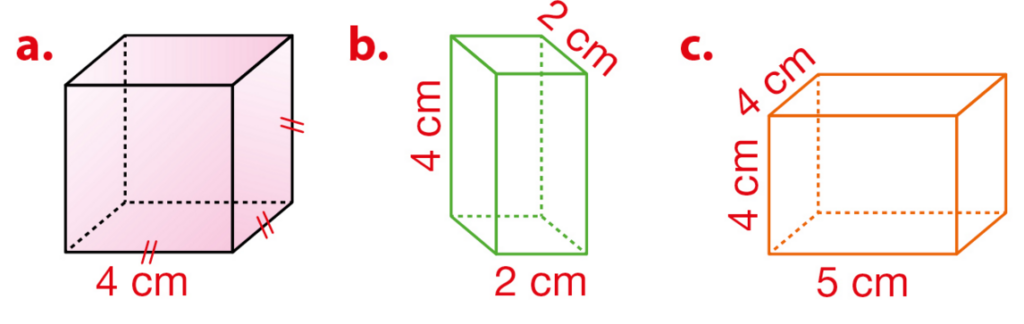
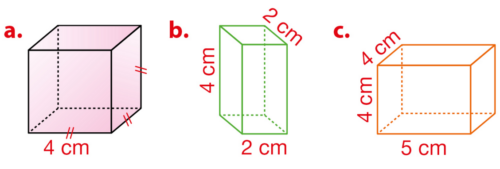
Calculer le volume de chaque parallélépipède rectangle.
Exercice 31 :
Parmi ces quatre solides, quel est celui qui a le plus grand volume ?
Exercice 32 :
Effectuer les conversions de volumes suivantes :
Exercice 33 :
Un aquarium a une longueur de 80 cm et une largeur de 30 cm.
II contient 35 cm de hauteur d’eau.
a. Calculer le volume d’eau, en , contenue dans cet aquarium.
b. Combien de litres d’eau a-t-on versés dans cet aquarium ?

Exercice 34 :
Cette tente a la forme d’un prisme droit.
a. Calculer son volume.
b. Donner sa contenance en litres.
Exercice 35 :
Un gâteau cuit dans un moule cylindrique de diamètre 22 cm et de hauteur 6 cm.
Ce gâteau est partagé équitablement en 7 parts.
Calculer une valeur approchée au dixième prés du volume, en , de chaque part.

Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «volumes : exercices de maths en 5ème corrigés en PDF.» au format PDF.
Ressources de cinquième
Cours de cinquième
Exercices de cinquième
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.