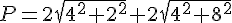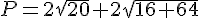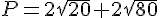Racine carrée : corrigé des exercices de maths en 2de en PDF.

Mis à jour le 28 avril 2025

🔍Corrigés Détaillés

2de • Scolaire

Racine carrée

🔎 Analyse : 17 min

🎯 Niveau : Scolaire

📱 Format : Gratuit

📄 PDF : Disponible

Le corrigé des exercices de maths en 2de sur les racinés carrées. Connaître la définition d’une racine carrée et savoir appliquer les formules du produit, du quotient de deux racines carrées en seconde.

Exercice 1 :

On pose 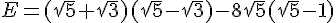$E=(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})-8\sqrt{5}(\sqrt{5}-1)$ .

Ecrire E sous forme 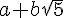$a+b\sqrt{5}$ .

( a et b étant des nombres relatifs) .

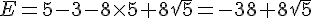
$E=5-3-8\times 5 +8\sqrt{5}=-38+8\sqrt{5}$

Exercice 2 :
Calculer D et E et donner les résultats sous la forme 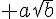$a\sqrt{b}$ où a et b sont des nombres entiers avec b le plus petit possible.

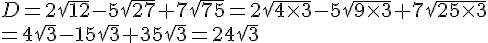
$D=2\sqrt{12}-5\sqrt{27}+7\sqrt{75}=2\sqrt{4\times 3}-5\sqrt{9\times 3}+7\sqrt{25\times 3}\\=4\sqrt{3}-15\sqrt{3}+35\sqrt{3}=24\sqrt{3}$

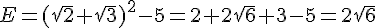
$E=(\sqrt{2}+\sqrt{3})^2-5=2+2\sqrt{6}+3-5=2\sqrt{6}$

Exercice 3 :
On donne :

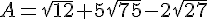
$A=\sqrt{12}+5\sqrt{75}-2\sqrt{27}$

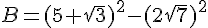
$B=(5+\sqrt{3})^2-(2\sqrt{7})^2$

Ecrire A sous la forme 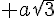$a\sqrt{3}$ et B sous la forme 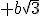$b\sqrt{3}$ où a et b sont deux entiers relatifs .

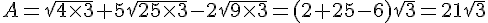
$A=\sqrt{4\times 3}+5\sqrt{25\times 3}-2\sqrt{9\times 3}=(2+25-6)\sqrt{3}=21\sqrt{3}$

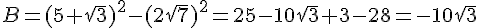
$B=(5+\sqrt{3})^2-(2\sqrt{7})^2=25-10\sqrt{3}+3-28=-10\sqrt{3}$

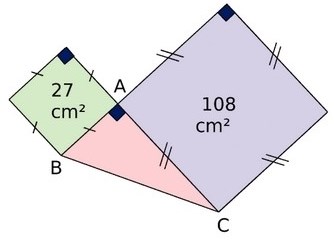
Exercice 4 :

1. On a:

a² = 3(1 + 2√6 + 6) = 21 + 6√6

b² = (3 – √6)² = 9 – 6√6 + 6 = 15 – 6√6

a² + b² = 36 + 15 = 51

2. Pour montrer que a² + b² est un nombre entier, il suffit de remarquer que (a² + b²) est égal à l’opposé du coefficient de √6 dans les expressions de a et b. En effet, on a :

a² + b² = (21 + 6√6) + (15 – 6√6) = 36

Donc a² + b² est un nombre entier.

3. Si a et b sont les longueurs des côtés de l’angle droit dans un triangle rectangle, l’hypoténuse c aura une longueur telle que :

c² = a² + b²

En utilisant les valeurs trouvées précédemment, on a :

c² = 21 + 6√6 + 15 – 6√6 = 36

Donc c = 6.

Donc si a et b sont les longueurs des côtés de l’angle droit dans un triangle rectangle, l’hypoténuse a une longueur de 6.

Exercice 5 :

Une pièce rectangulaire dont la longueur est le double de la largeur a une aire de 12,5 m².

Quelles sont ses dimensions?

Notons la largeur de cette pièce rectangulaire.

Nous obtenons :

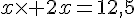
$x\times 2x=12,5$

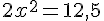
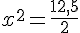
$x^2=\frac{12,5}{2}$

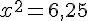
donc soit

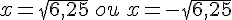
$x=\sqrt{6,25}\,ou\,x=-\sqrt{6,25}$

or est une largeur donc un nombre positif.

donc

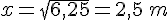
$x=\sqrt{6,25}=2,5\,m$

Conclusion : la largeur de ce rectangle est de 2,5 m et sa longueur est de 5 m.

Exercice 6 :

1. Sans calculer leur PGCD, explique pourquoi les nombres 648 et 972 ne sont pas premiers entre eux.

Ces deux nombres sont pairs donc divisibles par 2 donc 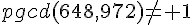$pgcd(648,972)\neq 1$ ainsi ces deux nombres

ne sont pas premiers entre eux.

2. a. Calculer PGCD ( 972 ; 648 ) en expliquant la méthode utilisée.

Utilisons l’algorithme d’Euclide.

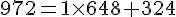
$972=1\times 648+324$

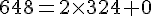
$648=2\times 324+0$

Le pgcd (972,648) est le dernier reste non nul donc .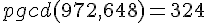

b. Démontrer que 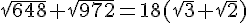$\sqrt{648}+\sqrt{972}=18(\sqrt{3}+\sqrt{2})$ .

En utilisant la question précédente :

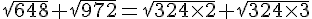
$\sqrt{648}+\sqrt{972}=\sqrt{324\times 2}+\sqrt{324\times 3}$

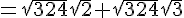
$=\sqrt{324}\sqrt{ 2}+\sqrt{324}\sqrt{3}$

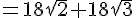
$=18\sqrt{ 2}+18\sqrt{3}$

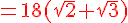
${\color{DarkRed} =18(\sqrt{ 2}+\sqrt{3})}$

Exercice 7 :

Dans le triangle AHC rectangle en H, d’après la partie directe

du théorème de Pythagore :

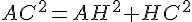
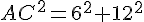
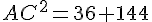
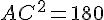
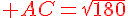
${\color{DarkRed} AC=\sqrt{180}}$

Exercice 8 :
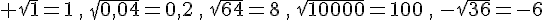
$\sqrt{1}=1\,,\,\sqrt{0,04}=0,2\,,\,\sqrt{64}=8\,,\,\sqrt{10000}=100\,,\,-\sqrt{36}=-6$

Exercice 9 :
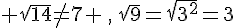
$\sqrt{14}\neq{7} \,,\,\sqrt{9}=\sqrt{3^2}=3\,$

Exercice 10 :
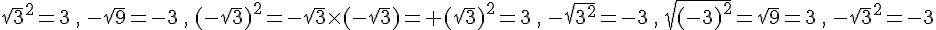${\sqrt{3}}^2=3\,,\,-\sqrt{9}=-3\,,\,(-\sqrt{3})^2=-\sqrt{3}\times (-\sqrt{3})=+(\sqrt{3})^2=3\,,\,-\sqrt{3^2}=-3\,,\,\sqrt{(-3)^2}=\sqrt{9}=3\,,\,-{\sqrt{3}}^2=-3$ .

Exercice 11 :
a. son côté mesure 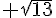$\sqrt{13}$ cm.

b. Son aire est 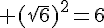$(\sqrt{6})^2=6$ cm².

Exercice 12 :
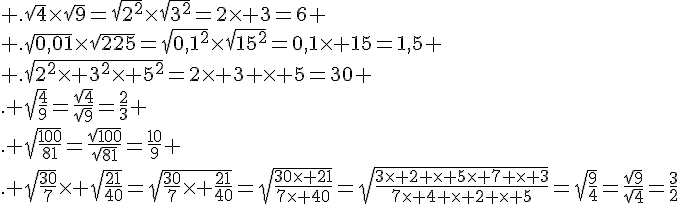
$.\sqrt{4}\times \sqrt{9}=\sqrt{2^2}\times \sqrt{3^2}=2\times 3=6 \\ .\sqrt{0,01}\times \sqrt{225}=\sqrt{0,1^2}\times \sqrt{15^2}=0,1\times 15=1,5 \\ .\sqrt{2^2\times 3^2\times 5^2}=2\times 3 \times 5=30 \\. \sqrt{\frac{4}{9}}=\frac{\sqrt{4}}{\sqrt{9}}=\frac{2}{3} \\. \sqrt{\frac{100}{81}}=\frac{\sqrt{100}}{\sqrt{81}}=\frac{10}{9} \\. \sqrt{\frac{30}{7}}\times \sqrt{\frac{21}{40}}=\sqrt{\frac{30}{7}\times \frac{21}{40}}=\sqrt{\frac{30\times 21}{7\times 40}}=\sqrt{\frac{3\times 2 \times 5\times 7 \times 3}{7\times 4 \times 2 \times 5}}=\sqrt{\frac{9}{4}}=\frac{\sqrt{9}}{\sqrt{4}}=\frac{3}{2}$

Exercice 13

a. On peut simplifier ces racines carrées :

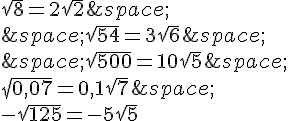
$\sqrt{8}=2\sqrt{2}\,\\\,\sqrt{54}=3\sqrt{6}\,\\\,\sqrt{500}=10\sqrt{5}\,\\\sqrt{0,07}=0,1\sqrt{7}\,\\-\sqrt{125}=-5\sqrt{5}$

b. On peut simplifier ces racines carrées :

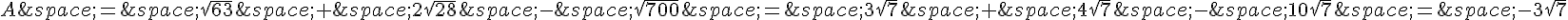
$A\,=\,\sqrt{63}\,+\,2\sqrt{28}\,-\,\sqrt{700}\,=\,3\sqrt{7}\,+\,4\sqrt{7}\,-\,10\sqrt{7}\,=\,-3\sqrt{7}$
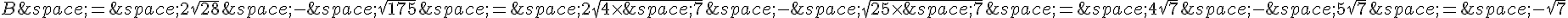
$B\,=\,2\sqrt{28}\,-\,\sqrt{175}\,=\,2\sqrt{4\times \,7}\,-\,\sqrt{25\times \,7}\,=\,4\sqrt{7}\,-\,5\sqrt{7}\,=\,-\sqrt{7}$

Exercice 14

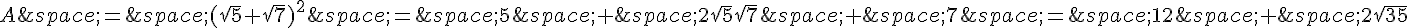
$A\,=\,(\sqrt{5}+\sqrt{7})^2\,=\,5\,+\,2\sqrt{5}\sqrt{7}\,+\,7\,=\,12\,+\,2\sqrt{35}$

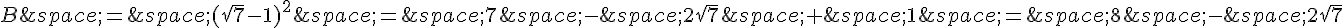
$B\,=\,(\sqrt{7}-1)^2\,=\,7\,-\,2\sqrt{7}\,+\,1\,=\,8\,-\,2\sqrt{7}$
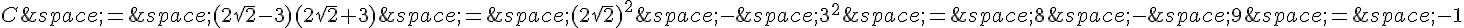
$C\,=\,(2\sqrt{2}-3)(2\sqrt{2}+3)\,=\,(2\sqrt{2})^2\,-\,3^2\,=\,8\,-\,9\,=\,-1$

Exercice 15

On explicite les racines carrées :

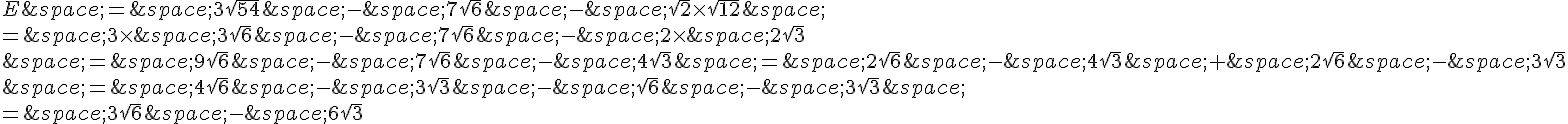
$E\,=\,3\sqrt{54}\,-\,7\sqrt{6}\,-\,\sqrt{2}\times \sqrt{12}\,\\=\,3\times \,3\sqrt{6}\,-\,7\sqrt{6}\,-\,2\times \,2\sqrt{3}\\\,=\,9\sqrt{6}\,-\,7\sqrt{6}\,-\,4\sqrt{3}\,=\,2\sqrt{6}\,-\,4\sqrt{3}\,+\,2\sqrt{6}\,-\,3\sqrt{3}\\\,=\,4\sqrt{6}\,-\,3\sqrt{3}\,-\,\sqrt{6}\,-\,3\sqrt{3}\,\\=\,3\sqrt{6}\,-\,6\sqrt{3}$

Or, on a :

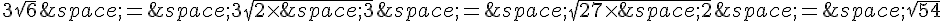
$3\sqrt{6}\,=\,3\sqrt{2\times \,3}\,=\,\sqrt{27\times \,2}\,=\,\sqrt{54}$

Donc :

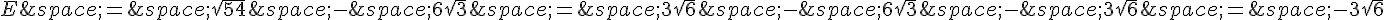
$E\,=\,\sqrt{54}\,-\,6\sqrt{3}\,=\,3\sqrt{6}\,-\,6\sqrt{3}\,-\,3\sqrt{6}\,=\,-3\sqrt{6}$

Exercice 16 :

On commence par construire un carré ADEF de côté 6 cm :

On marque le milieu I de [DE], puis on trace un arc de cercle de centre I et de rayon IF, où F est l’un des sommets du carré. Cet arc de cercle coupe le segment [AE] en un point B, et on trace la droite (BC) parallèle à (AD) passant par B. Cette droite coupe le segment [DE] en C, et on termine la construction en traçant la droite (AC) parallèle à (DE), qui coupe le côté [AE] du carré en D.

On veut montrer que ABCD est un rectangle d’or, c’est-à-dire que le quotient de sa longueur AB sur sa largeur BC est égal au nombre d’or.

On a AB = AE – EB et BC = CE, donc il nous faut exprimer ces deux longueurs en fonction de la longueur du côté du carré.

On a AE = 6 cm car AE est un côté du carré. On a aussi EB = IF, car EBIF est un rectangle, et IF est le rayon de l’arc de cercle tracé précédemment, donc

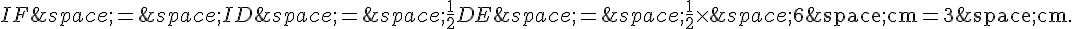
$IF\,=\,ID\,=\,\frac{1}{2}DE\,=\,\frac{1}{2}\times \,6\text{\,cm}=3\text{\,cm}.$

On a donc :

AB = AE – EB = 6 – 3 = 3 cm.

On a également CE = DE – DC.

Or, DC est la longueur de la projection de AD sur la droite (BC), donc (DC) est égal à la hauteur du triangle ABC par rapport au côté (AB).

Comme les droites (AB) et (BC) sont parallèles, on a :

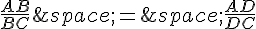
$\frac{AB}{BC}\,=\,\frac{AD}{DC}$

ou encore :

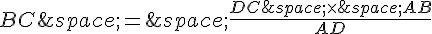
$BC\,=\,\frac{DC\,\times \,AB}{AD}$

Le triangle ABD est rectangle en D, donc on peut utiliser le théorème de Pythagore pour exprimer DC en fonction de AB et AD :

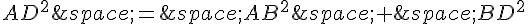
$AD^2\,=\,AB^2\,+\,BD^2$

Or, BD est un côté du carré DEFI, donc BD = 6 cm. On en déduit que :

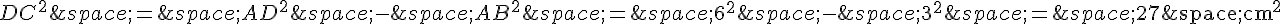
$DC^2\,=\,AD^2\,-\,AB^2\,=\,6^2\,-\,3^2\,=\,27\text{\,cm}^2$

On a donc :

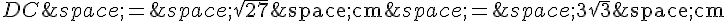
$DC\,=\,\sqrt{27}\text{\,cm}\,=\,3\sqrt{3}\text{\,cm}$

On en déduit que :

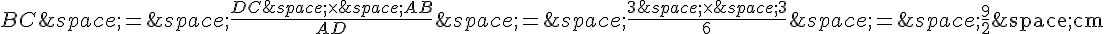
$BC\,=\,\frac{DC\,\times \,AB}{AD}\,=\,\frac{3\,\times \,3}{6}\,=\,\frac{9}{2}\text{\,cm}$

Finalement, le rapport AB/BC vaut :

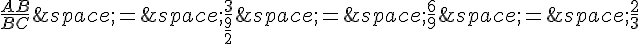
$\frac{AB}{BC}\,=\,\frac{3}{\frac{9}{2}}\,=\,\frac{6}{9}\,=\,\frac{2}{3}$

Or, le nombre d’or est égal à 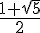$\frac{1+\sqrt{5}}{2}$ , qui est approximativement égal à 1,618.

On a 2/3 < 1,618, donc le rapport 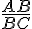$\frac{AB}{BC}$ ne vaut pas le nombre d’or. Cependant, le rectangle ABCD est très proche d’un rectangle d’or, et les mathématiciens de l’Antiquité et de la Renaissance ont utilisé cette construction pour créer des formes d’art et d’architecture qui s’approchent le plus possible de la proportion divine du nombre d’or.

Exercice 17 :

a) On factorise les radicaux :

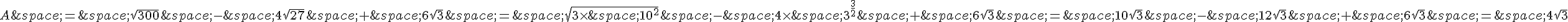
$A\,=\,\sqrt{300}\,-\,4\sqrt{27}\,+\,6\sqrt{3}\,=\,\sqrt{3\times \,10^2}\,-\,4\times \,3^{\frac{3}{2}}\,+\,6\sqrt{3}\,=\,10\sqrt{3}\,-\,12\sqrt{3}\,+\,6\sqrt{3}\,=\,4\sqrt{3}$

Donc A peut être écrit sous la forme 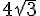$4\sqrt{3}$ .

b) On développe B :

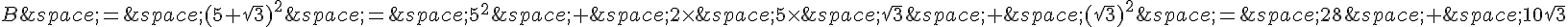
$B\,=\,(5+\sqrt{3})^2\,=\,5^2\,+\,2\times \,5\times \,\sqrt{3}\,+\,(\sqrt{3})^2\,=\,28\,+\,10\sqrt{3}$

Donc B peut être écrit sous la forme 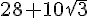$28+10\sqrt{3}$ .

c) On utilise l’identité remarquable 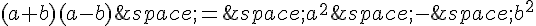$(a+b)(a-b)\,=\,a^2\,-\,b^2$ :

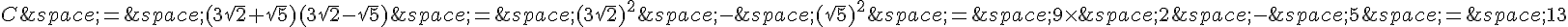
$C\,=\,(3\sqrt{2}+\sqrt{5})(3\sqrt{2}-\sqrt{5})\,=\,(3\sqrt{2})^2\,-\,(\sqrt{5})^2\,=\,9\times \,2\,-\,5\,=\,13$

Donc C est un entier.

Exercice 18 :

Démontrer, sans utiliser la calculatrice, que :

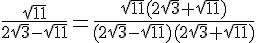
$\frac{\sqrt{11}}{2\sqrt{3}-\sqrt{11}}=\frac{\sqrt{11}(2\sqrt{3}+\sqrt{11})}{(2\sqrt{3}-\sqrt{11})(2\sqrt{3}+\sqrt{11})}$

Utilisons l’identité remarquable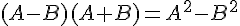

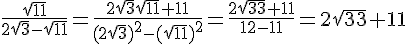
$\frac{\sqrt{11}}{2\sqrt{3}-\sqrt{11}}= \frac{2\sqrt{3}\sqrt{11}+11}{(2\sqrt{3})^2-(\sqrt{11})^2}= \frac{2\sqrt{33}+11}{12-11}=2\sqrt{33}+11$

Exercice 19 :

Développer et donner le résultat sous la forme

la plus simplifiée possible .

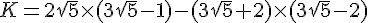
$K=2\sqrt{5}\times (3\sqrt{5}-1)-(3\sqrt{5}+2)\times (3\sqrt{5}-2)$

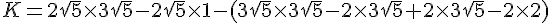
$K=2\sqrt{5}\times 3\sqrt{5}-2\sqrt{5}\times 1-(3\sqrt{5}\times 3\sqrt{5}-2\times 3\sqrt{5}+2\times 3\sqrt{5}-2\times 2)$

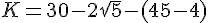
$K=30-2\sqrt{5}-(45-4)$

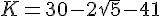
$K=30-2\sqrt{5}-41$

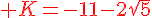
${\color{DarkRed} K=-11-2\sqrt{5}}$

Exercice 20 :

Développer et réduire cette expression :

A = (2 7 -9)(2 7 )+9

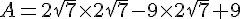
$A=2\sqrt{7}\times 2\sqrt{7}-9\times 2\sqrt{7}+9$

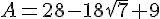
$A=28-18\sqrt{7}+9$

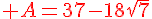
${\color{DarkRed} A=37-18\sqrt{7}}$

Exercice 21 :

Soient trois points O, U et I tels que : $UI=\sqrt{63}$ ; $OU=\sqrt{343}$ et $OI=\sqrt{700}$ .

Les points O, U et I sont-ils alignés ? Justifier.

Si les points sont alignés alors la plus grande distance étant OI nous aurions OI=UI+OU .

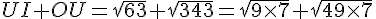
$UI+OU=\sqrt{63}+\sqrt{343}=\sqrt{9\times 7}+\sqrt{49\times 7}$

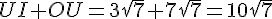
$UI+OU=3\sqrt{7}+7\sqrt{7}=10\sqrt{7}$

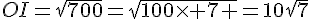
$OI=\sqrt{700}=\sqrt{100\times 7 }=10\sqrt{7}$

Conclusion : OI=UI+OU donc les trois points sont alignés .

Exercice 22 :

Développer et réduire les expressions suivantes et donne le résultat sous la forme 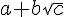$a+b\sqrt{c}$ ,

où a et b sont des entiers relatifs et c un nombre entier positif.

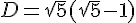
$D=\sqrt{5}(\sqrt{5}-1)$

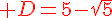
${\color{DarkRed} D=5-\sqrt{5}}$

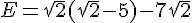
$E=\sqrt{2}(\sqrt{2}-5)-7\sqrt{2}$

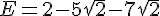
$E=2-5\sqrt{2}-7\sqrt{2}$

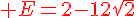
${\color{DarkRed} E=2-12\sqrt{2}}$

Exercice 23 :

Exprimer les aires de ces trois rectangles sous la forme 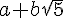$a+b\sqrt{5}$

(où 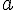et 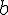sont des nombres entiers ).

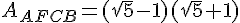
$A_{AFCB}=(\sqrt{5}-1)(\sqrt{5}+1)$

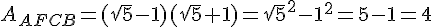
$A_{AFCB}=(\sqrt{5}-1)(\sqrt{5}+1)=\sqrt{5}^2-1^2=5-1=4$

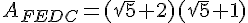
$A_{FEDC}=(\sqrt{5}+2)(\sqrt{5}+1)$

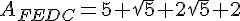
$A_{FEDC}=5+\sqrt{5}+2\sqrt{5}+2$

${\color{DarkRed} A_{FEDC}=7+3\sqrt{5}}$

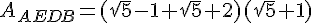
$A_{AEDB}=(\sqrt{5}-1+\sqrt{5}+2)(\sqrt{5}+1)$

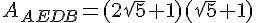
$A_{AEDB}=(2\sqrt{5}+1)(\sqrt{5}+1)$

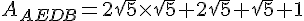
$A_{AEDB}=2\sqrt{5}\times \sqrt{5}+2\sqrt{5}+\sqrt{5}+1$

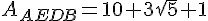
$A_{AEDB}=10+3\sqrt{5}+1$

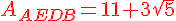
${\color{DarkRed} A_{AEDB}=11+3\sqrt{5}}$

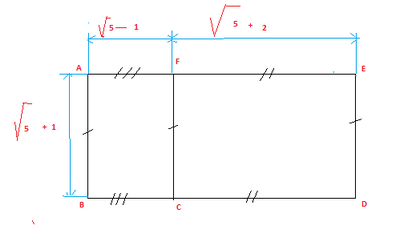
Exercice 24 :

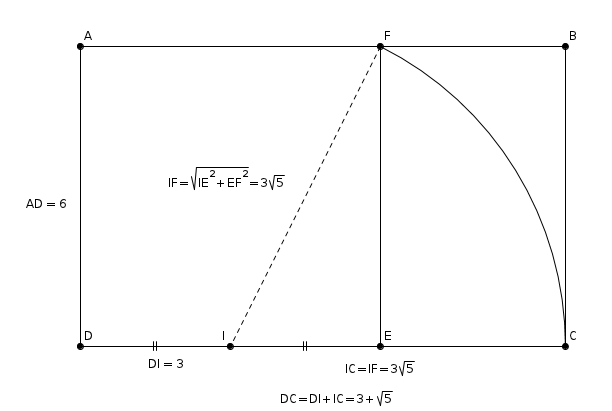
Dans le triangle OAB rectangle en B, d’après la partie directe du théorème de Pythagore :

Le triangle est isocèle en O.

La droite (OB) est une hauteur mais aussi une médiatrice donc B est situé au milieu du segment .

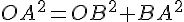
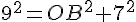
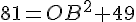
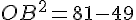
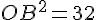
OB^2=32

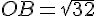
$OB=\sqrt{32}$

Conclusion : la hauteur maximale est 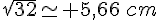$\sqrt{32}\simeq 5,66\,cm$

Exercice 25 :

Montrez en appliquant le théorème de Pythagore dans le triangle rectangle GCD que :

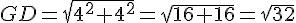
$GD=\sqrt{4^2+4^2}=\sqrt{16+16}=\sqrt{32}$

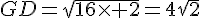
$GD=\sqrt{16\times 2}=4\sqrt{2}$

Le périmètre est 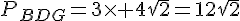$P_{BDG}=3\times 4\sqrt{2}=12\sqrt{2}$ car BDG est un triangle équilatéral.

(GK) est une hauteur mais également une médiatrice de [DB]

car GDB est un triangle équilatéral.

En appliquant le théorème de Pythagore dans GBK rectangle en K :

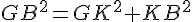
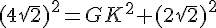
$(4\sqrt{2})^2=GK^2+(2\sqrt{2})^2$

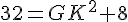
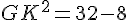
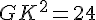
GK^2=24

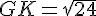
$GK=\sqrt{24}$

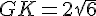
$GK=2\sqrt{6}$

$A_{BGD}=\frac{BD\times KG}{2}=\frac{4\sqrt{2}\times 2\sqrt{6}}{2}$

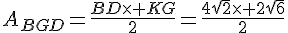
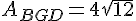
$A_{BGD}=4\sqrt{12}$

${\color{DarkRed} A_{BGD}=8\sqrt{3}}$

Exercice 26 :

Appliquez le théorème de Pythagore dans les triangles rectangles successifs et montrez que :

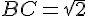
$BC=\sqrt{2}$

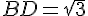
$BD=\sqrt{3}$

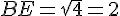
$BE=\sqrt{4}=2$

Exercice 27 :

a. AMI est un triangle rectangle isocèle,

d’après la partie directe du théorème de Pythagore :

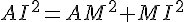
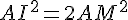
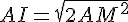
$AI=\sqrt{2AM^2}$

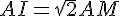
$AI=\sqrt{2}AM$

En conclusion la diagonale d’un carré mesure 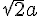$\sqrt{2}a$ si la longueur du côté est .

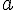Exercice 28 :

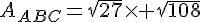
$A_{ABC}=\sqrt{27}\times \sqrt{108}$

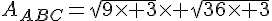
$A_{ABC}=\sqrt{9\times 3}\times \sqrt{36\times 3}$

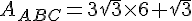
$A_{ABC}=3\sqrt{3}\times 6 \sqrt{3}$

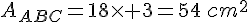
$A_{ABC}=18\times 3=54\,cm^2$

Exercice 29 :

Développer et réduire : 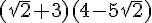$(\sqrt{2}+3)(4-5\sqrt{2})$ .

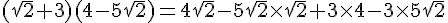
$(\sqrt{2}+3)(4-5\sqrt{2})=4\sqrt{2}-5\sqrt{2}\times \sqrt{2}+3\times 4-3\times 5\sqrt{2}$

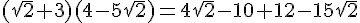
$(\sqrt{2}+3)(4-5\sqrt{2})=4\sqrt{2}-10+12-15\sqrt{2}$

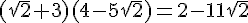
$(\sqrt{2}+3)(4-5\sqrt{2})=2-11\sqrt{2}$

Exercice 30 :

Développez en utilisant les identités remarquables :

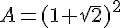
$A=(1+\sqrt{2})^2$

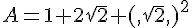
$A=1+2\sqrt{2}+,(,\sqrt{2},,)^2$

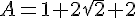
$A=1+2\sqrt{2}+2$

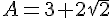
$A=3+2\sqrt{2$

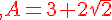
${\color{DarkRed},A=3+2\sqrt{2}}$

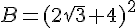
$B=(2\sqrt{3}+4)^2$

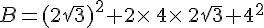
$B=(2\sqrt{3})^2+2\times \,4\times \,2\sqrt{3}+4^2$

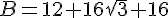
$B=12+16\sqrt{3}+16$

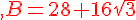
${\color{DarkRed},B=28+16\sqrt{3}}$

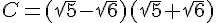
$C=(\sqrt{5}-\sqrt{6})(\sqrt{5}+\sqrt{6})$

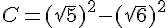
$C=(\sqrt{5})^2-(\sqrt{6})^2$

C=5-6

${\color{DarkRed},C=-1}$

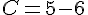
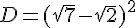
$D=(\sqrt{7}-\sqrt{2})^2$

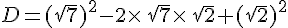
$D=(\sqrt{7})^2-2\times \,\sqrt{7}\times \,\sqrt{2}+(\sqrt{2})^2$

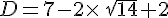
$D=7-2\times \,\sqrt{14}+2$

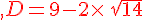
${\color{DarkRed},D=9-2\times \,\sqrt{14}}$

Exercice 31 :

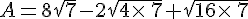
$A=8\sqrt{7}-2\sqrt{4\times \,7}+\sqrt{16\times \,7}$

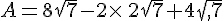
$A=8\sqrt{7}-2\times \,2\sqrt{7}+4\sqrt{,7}$

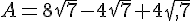
$A=8\sqrt{7}-4\sqrt{7}+4\sqrt{,7}$

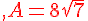
${\color{DarkRed},A=8\sqrt{7}}$

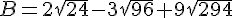
$B=2\sqrt{24}-3\sqrt{96}+9\sqrt{294}$

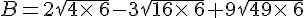
$B=2\sqrt{4\times \,6}-3\sqrt{16\times \,6}+9\sqrt{49\times \,6}$

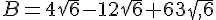
$B=4\sqrt{6}-12\sqrt{6}+63\sqrt{,6}$

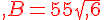
${\color{DarkRed},B=55\sqrt{,6}}$

Exercice 32 :

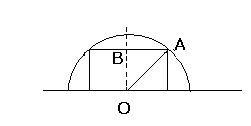
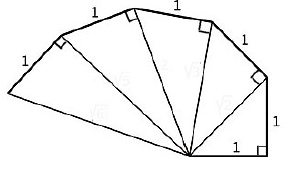
En appliquant le théorème de Pythagore.

Vous vous apercevrez que :

– l’hypoténuse du premier triangle rectangle mesure 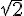$\sqrt{2}$

– l’hypoténuse du second triangle rectangle mesure 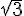$\sqrt{3}$

– l’hypoténuse du troisième triangle rectangle mesure 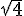$\sqrt{4}$

– l’hypoténuse du quatrième triangle rectangle mesure 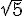$\sqrt{5}$

– l’hypoténuse du cinquième triangle rectangle mesure 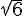$\sqrt{6}$

Donc l’hypoténuse du septième triangle rectangle mesurera 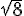$\sqrt{8}$ .

Exercice 33 :

On considère la fonction h telle que .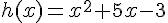

1. Calculer l’image de 1 par la fonction h.

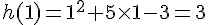
$h(1)=1^2+5\times 1-3=3$

2. Calculer l’image de 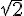$\sqrt{2}$ par la fonction h.

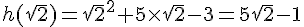
$h(\sqrt{2})=\sqrt{2}^2+5\times \sqrt{2}-3=5\sqrt{2}-1$

3. Calculer l’image de 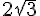$2\sqrt{3}$ par la fonction h.

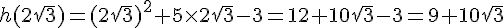
$h(2\sqrt{3})=(2\sqrt{3})^2+5\times 2\sqrt{3}-3=12+10\sqrt{3}-3=9+10\sqrt{3}$

Exercice 34 :

Un verre de la forme conique a une hauteur de 11 cm.

Quelle doit être la valeur exacte de la longueur de son diamètre, en cm, pour qu’il

contienne 25 cL ?

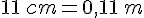
$11\,cm=0,11\,m$

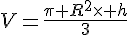
$V=\frac{\pi R^2\times h}{3}$

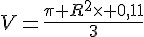$V=\frac{\pi R^2\times 0,11}{3}$ ce volume sera en 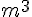m^3 avec 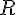en mètre.

Or 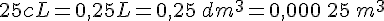$25cL=0,25L=0,25\,dm^3=0,000\,25\,m^3$

d’où

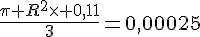
$\frac{\pi R^2\times 0,11}{3}=0,00025$

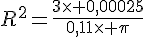$R^2=\frac{3\times 0,00025}{0,11\times \pi}$ or R est un nombre positif donc :

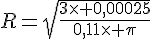
$R=\sqrt{\frac{3\times 0,00025}{0,11\times \pi}}$

donc la valeur exacte du diamètre doit être :

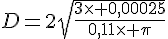
$D=2\sqrt{\frac{3\times 0,00025}{0,11\times \pi}}$

Exercice 35 : En utilisant Pythagore :le périmètre est : $P=2\sqrt{4^2+2^2}+2\sqrt{4^2+8^2}$ $P=2\sqrt{20}+2\sqrt{16+64}$ $P=2\sqrt{20}+2\sqrt{80}$

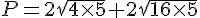
$P=2\sqrt{4\times 5}+2\sqrt{16\times 5}$

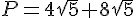
$P=4\sqrt{5}+8\sqrt{5}$

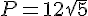
$P=12\sqrt{5}$

Exercice 36 :

a. 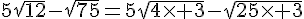$5\sqrt{12}-\sqrt{75}=5\sqrt{4\times 3}-\sqrt{25\times 3}$

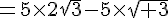
$=5\times 2\sqrt{3}-5\times \sqrt{ 3}$

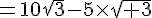
$=10\sqrt{3}-5\times \sqrt{ 3}$

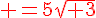
${\color{DarkRed} =5\sqrt{ 3}}$

b. ABCD est un carré car AB=AD les côtés opposés sont parallèles et il possède 4 angles droits.

Exercice 37 :

Écrire sous la forme 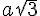$a\sqrt{3}$ , a étant un entier naturel:

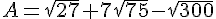$A=\sqrt{27}+7\sqrt{75}-\sqrt{300}$ .

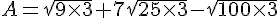
$A=\sqrt{9\times 3}+7\sqrt{25\times 3}-\sqrt{100\times 3}$

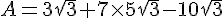
$A=3\sqrt{3}+7\times 5\sqrt{3}-10\sqrt{3}$

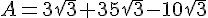
$A=3\sqrt{3}+35\sqrt{3}-10\sqrt{3}$

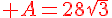
${\color{DarkRed} A=28\sqrt{3}}$

Ecrire sous la forme 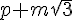$p+m\sqrt{3}$ ou m et p sont des entiers relatifs :

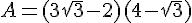
$A=(3\sqrt{3}-2)(4-\sqrt{3})$

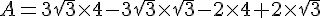
$A=3\sqrt{3}\times 4-3\sqrt{3}\times \sqrt{3}-2\times 4+2\times \sqrt{3}$

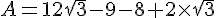
$A=12\sqrt{3}-9-8+2\times \sqrt{3}$

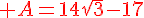
${\color{DarkRed} A=14\sqrt{3}-17}$

Exercice 38 :

Mettre les nombres suivants sous la forme 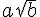$a\sqrt{b}$

où 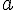et 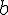sont deux nombres entiers et 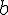le plus petit possible .

$t=\sqrt{96}\,\,\,;\,\,\,u=\sqrt{108}\,\,\,;\,\,\,v=\sqrt{162}$

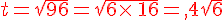
$t=\sqrt{96}=\sqrt{6\times \,16}={\color{DarkRed},4\sqrt{6}}$

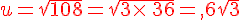
$u=\sqrt{108}=\sqrt{3\times \,36}={\color{DarkRed},6\sqrt{3}}$

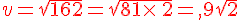
$v=\sqrt{162}=\sqrt{81\times \,2}={\color{DarkRed},9\sqrt{2}}$

Exercice 39 :

Mettre les nombres suivants sous la forme $a\sqrt{5}$ .

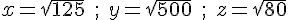
$x=\sqrt{125}\,\,\,;\,\,\,y=\sqrt{500}\,\,\,;\,\,\,z=\sqrt{80}$

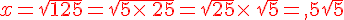$x=\sqrt{125}=\sqrt{5\times \,25}=\sqrt{25}\times \,\sqrt{5}={\color{DarkRed},5\sqrt{5}}$ .

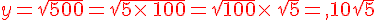
$y=\sqrt{500}=\sqrt{5\times \,100}=\sqrt{100}\times \,\sqrt{5}={\color{DarkRed},10\sqrt{5}}$

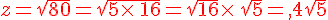
$z=\sqrt{80}=\sqrt{5\times \,16}=\sqrt{16}\times \,\sqrt{5}={\color{DarkRed},4\sqrt{5}}$

Exercice 40 :

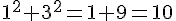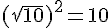Ce triangle est rectangle car et $(\sqrt{10})^2=10$ .

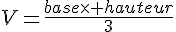
$V=\frac{base\times hauteur}{3}$

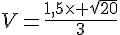
$V=\frac{1,5\times \sqrt{20}}{3}$

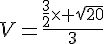
$V=\frac{\frac{3}{2}\times \sqrt{20}}{3}$

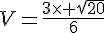
$V=\frac{3\times \sqrt{20}}{6}$

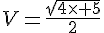
$V=\frac{\sqrt{4\times 5}}{2}$

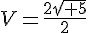
$V=\frac{2\sqrt{ 5}}{2}$

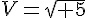
$V=\sqrt{ 5}$

Exercice 41 :

Calculer la longueur du segment [AC ] .

Dans les triangles ABC et EDC,

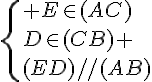
$\{ E\in(AC)\\D\in(CB) \\(ED)//(AB).$

d’après la partie directe du théorème de Thalès :

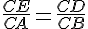
$\frac{CE}{CA}=\frac{CD}{CB}$

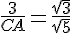
$\frac{3}{CA}=\frac{\sqrt{3}}{\sqrt{5}}$

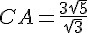
$CA=\frac{3\sqrt{5}}{\sqrt{3}}$

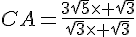
$CA=\frac{3\sqrt{5}\times \sqrt{3}}{\sqrt{3}\times \sqrt{3}}$

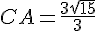
$CA=\frac{3\sqrt{15}}{3}$

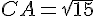
$CA=\sqrt{15}$

Exercice 42 :

Propriété : un produit de facteurs est nul si et seulement l’un des facteurs, au moins, est nul .

a) 3x² =75

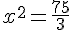
$x^2=\frac{75}{3}$

x^2=25

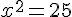
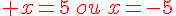
${\color{DarkRed} x=5\,ou\,x=-5}$

b) x²= -36

Pas de solution un carré est positif ou nul .

c) 25x² =4

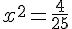
$x^2=\frac{4}{25}$

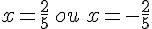
$x=\frac{2}{5}\,ou\,x=-\frac{2}{5}$

d) 49x² = -64

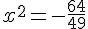
$x^2=-\frac{64}{49}$

Pas de solution, un carré est positif ou nul .

e) x²+9=0

x^2=-9

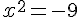
Pas de solution, un carré est positif ou nul .

f) 27x² = 12

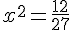
$x^2=\frac{12}{27}$

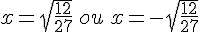
$x=\sqrt{\frac{12}{27}}\,ou\,x=-\sqrt{\frac{12}{27}}$

Exercice 43 :

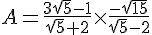
$A=\frac{3\sqrt{5}-1}{\sqrt{5}+2}\times \frac{-\sqrt{15}}{\sqrt{5}-2}$

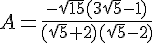
$A=\frac{-\sqrt{15}(3\sqrt{5}-1)}{(\sqrt{5}+2)(\sqrt{5}-2)}$

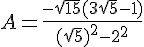
$A=\frac{-\sqrt{15}(3\sqrt{5}-1)}{(\sqrt{5})^2-2^2}$

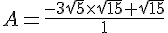
$A=\frac{-3\sqrt{5}\times \sqrt{15}+\sqrt{15}}{1}$

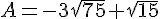
$A=-3\sqrt{75}+\sqrt{15}$

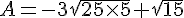
$A=-3\sqrt{25\times 5}+\sqrt{15}$

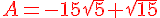
${\color{DarkRed} A=-15\sqrt{5}+\sqrt{15}}$

Exercice 44 :

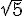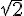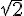Soit a= $\sqrt{5}$ (1- $\sqrt{2}$ ) et b=5+ $\sqrt{2}$ .

a. Calculer a² et b².

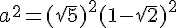
$a^2=(\sqrt{5})^2(1-\sqrt{2})^2$

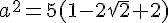
$a^2=5(1-2\sqrt{2}+2)$

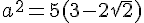
$a^2=5(3-2\sqrt{2})$

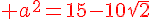
${\color{DarkRed} a^2=15-10\sqrt{2}}$

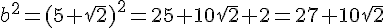
$b^2=(5+\sqrt{2})^2=25+10\sqrt{2}+2=27+10\sqrt{2}$

b. En déduire les valeurs de a²+b² et 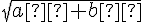$\sqrt{a²+b²}$ .

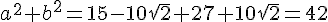
$a^2+b^2=15-10\sqrt{2}+27+10\sqrt{2}=42$

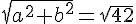
$\sqrt{a^2+b^2}=\sqrt{42}$

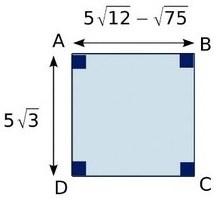
Exercice 45:

ABCD est un rectangle tel que :

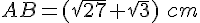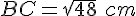$AB=(\sqrt{27}+\sqrt{3})\,\,cm$ et $BC=\sqrt{48}\,\,cm$ .

a) Démontrer que ABCD est un carré .

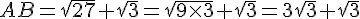
$AB=\sqrt{27}+\sqrt{3}=\sqrt{9\times 3}+\sqrt{3}=3\sqrt{3}+\sqrt{3}$

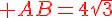
${\color{DarkRed} AB=4\sqrt{3}}$

$BC=\sqrt{48}=\sqrt{16\times 3}={\color{Red} 4\sqrt{3}}$

donc AB=BC ainsi ABCD est un carré.

b) calculer son périmètre et son aire .

Périmètre = 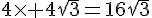$4\times 4\sqrt{3}=16\sqrt{3}$ cm

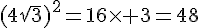Aire = $(4\sqrt{3})^2=16\times 3=48$ cm².

4.4/5 - (23259 votes)

Télécharger et imprimer ce document en PDF gratuitement :

Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «racine carrée : corrigé des exercices de maths en 2de en PDF.» au format PDF.

Ressources de seconde

Cours de seconde

Position relative d’une droite et d’un plan dans l’espace

Nombres entiers et rationnels et calcul du PGCD

Les fonctions numériques

Généralités sur les fonctions numériques

Ensembles de nombres et calculs

Racine carrée

Exercices de seconde

Vecteurs et translation

Fonctions

Systèmes de deux équations

Géométrie dans l’espace

Probabilités

Les inéquations

×12

L'équipe Mathovore

Contenu mis à jour quotidiennement

12 Enseignants Titulaires

Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.

12 Professeurs

200+ Années cumulées

Quotidien Mise à jour

Nos applications

Téléchargez gratuitement la dernière version de nos applications.

Mathovore c'est 14 122 542 cours et exercices de maths téléchargés en PDF.