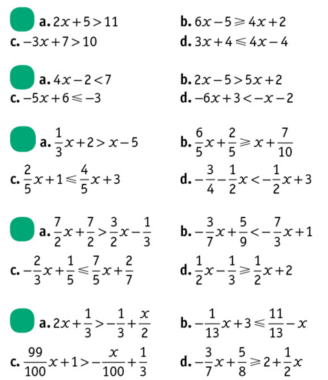Les inéquations : exercices de maths en 2de corrigés en PDF.
Mis à jour le 20 décembre 2025
Exercice 1 – Résoudre les inéquations suivantes
a.
b.
c.
Exercice 2 – Inéquations à résoudre
Résolvez les inéquations suivantes :
1) .
2)
3)
4)
5)
6)
Exercice 3 – Problème de périmètre
Le périmètre d’un rectangle est inférieur ou égal à 37 cm.
Sachant que sa largeur est égale à 5,3 cm, déterminer les valeurs possibles pour la
longueur de ce rectangle.
(La longueur doit être supérieure à la largeur)
Exercice 4 – Somme de 3 entiers consécutifs
La somme de trois entiers consécutifs est comprise entre 12 et 27.
Quelles sont les valeurs possibles du plus grand de ces trois nombres ?
Exercice 5 – Droite graduée
Représenter sur une droite graduée les solutions de l’inéquation :
-2x+7 < 5x + 29.
Exercice 6 – Problème de formule d’abonnement dans un parc de loisir
Un parc de loisir propose deux formules d’abonnement :
Formule A : La carte à l’année coûte 55 € et le prix d’une entrée est de 20 € .
Formule B : La carte à l’année coûte 80 € et le prix d’une entrée est de 15 € .
On note y le nombre d’entrées .
1. Exprimer, en fonction de y, le coût à l’année avec la formule A .
2. Exprimer, en fonction de y, le coût à l’année avec la formule B .
3. A partir de combien d’entrées dans l’année, la formule B se révèle-t-elle
la plus intéressante ?
Exercice 7 – Inéquation du premier degré
On considère l’inéquation :
1. Justifier que 0 est solution de cette inéquation .
2. est-il solution de cette inéquation ?
3. Après avoir développé le second membre, résolvez cette inéquation.
Exercice 8 :
Résoudre les inéquations suivantes où x est l’inconnue réelle :
a. x-4>0
b. x+7>9
c. x-3<6
d. x-8<-10
Exercice 9 :
Résoudre les inéquations suivantes où x est l’inconnue réelle :
a. 3x < 6
b. 2x>5
c. -5x < 15
d. -7x > 28
Exercice 10 :
Pour les réels x et y, si x < 5 et y < 7, quelle inégalité peut-on écrire dans chaque cas ?
a. 5x
b. 2x+y
c. x+2y
d. x+y
Exercice 11 :
Pour les réels x et y, si x < 2 et y > 1, quelle inégalité peut-on écrire dans chaque cas ?
a. 2x
b. -y
c. 2x-y
d. x-y
Exercice 12 :
Résoudre chaque inéquation.
On notera S l’ensemble des solutions et on représentera S sur l’axe des réels.
Exercice 13 :
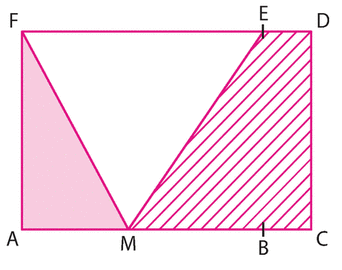
ACDF est un rectangle tel que AC = 6 et AF = 4.
B [AC] et E
[FD] tels que CB = 1 et DE= 1.
M est un point quelconque du segment [AB].
Morgan veut chercher à quelle distance du point A il doit placer le point M
pour que l’aire hachurée soit supérieure ou égale à l’aire du triangle AMF.
Quelle inéquation doit-il poser et résoudre pour répondre à ce problème ?
Exercice 14 :
Un trajet en train entre deux villes de France coûte
9,10 euros (aller simple) si on achète une carte de réduction valant 30 euros, au lieu de 12,70 euros
(aller simple) au tarif normal. Lilia consacre un budget d’au plus 140 euros pour ses trajets entre ces deux villes. Elle possède la carte de réduction.
Quelle inéquation doit-elle résoudre pour connaître le nombre de trajets au maximum qu’elle peut faire
avec son budget ?
Exercice 15 :
Théo roule à une vitesse comprise entre 15 et 17 km/h sur son vélo.
Quelle distance peut-il avoir parcourue en 3 h 30 min ?
Exercice 16 :
Tom sait que le bénéfice (en euros), de sa dernière vente de chocolats est
compris dans l’intervalle [190 ; 200].
De plus, il sait que le bénéfice y de sa dernière vente de jus de pommes est tel que .
L’année prochaine, il prévoit de multiplier les bénéfices de sa vente de chocolats par 1,3 et
les bénéfices de sa vente de jus de pommes par 1,2.
Déterminer un encadrement de son bénéfice total pour l’année prochaine.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «les inéquations : exercices de maths en 2de corrigés en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
L'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.