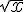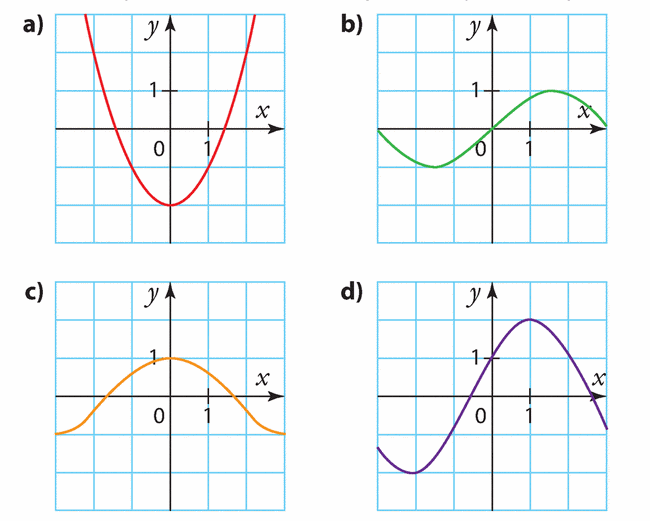Équations et inéquations : exercices de maths en 2de corrigés en PDF.
Mis à jour le 12 décembre 2025
Exercice 1 – Racine d’un polynôme et factorisation
On pose 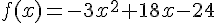 .
.
1. Trouver une racine évidente de  , c’est à dire une valeur
, c’est à dire une valeur  telle que
telle que 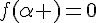 .
.
2. En déduire une factorisation de 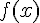 .
.
3. Résoudre l’inéquation  .
.
Exercice 2 – Les inéquations
Résoudre les inéquations suivantes et décrire sur une droite graduée l’ensemble solution :
a. 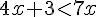 .
.
b.  .
.
c. 4x+3 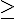 7x+8.
7x+8.
d. 4x+3 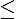 7(x+8).
7(x+8).
e. 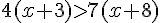 .
.
f. -4x+3 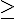 7x-8.
7x-8.
g. -4(x+3) 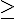 7(x-8).
7(x-8).
h. -4(x-3) 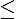 7x+8.
7x+8.
i. 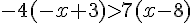 .
.
j. 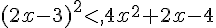
k. 
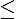
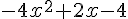
l. 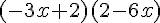
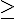
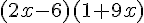
Exercice 3 – Résoudre l’équation suivante :
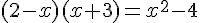
Exercice 4 – Résoudre une équation trigonométrique
1. Résoudre dans l’intervalle  , l’équation
, l’équation 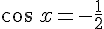 .
.
2. Résoudre dans l’intervalle 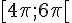 , l’équation
, l’équation 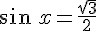 .
.
Conseil : servez-vous du cercle trigonométrique .
Exercice 5 – Inéquation rationnelle
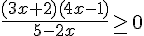
Exercice 6 – Equation avec fraction
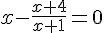
Exercice 7 – Passer de la forme canonique à la forme factorisée
Donner la forme factorisée de cette forme canonique :
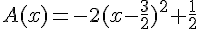
Exercice 8 – Equation complexe à résoudre
Résoudre l’équation suivante :

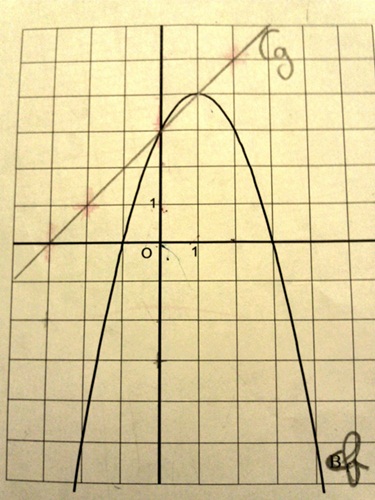
Exercice 9 – Résoudre graphiquement une équation et inéquation
1. Résoudre graphiquement l’équation 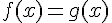 .
.
2. Résoudre graphiquement l’inéquation 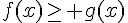 .
.
Exercice 10 – Equations produits à résoudre
Résoudre les équations suivantes
1. (x+4)² = (x+4) (3x+1)
2. (2x+1)² = (x+5)²
3. (x-2)²-2 = 2
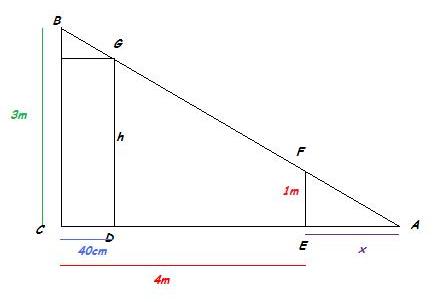
Exercice 11 – Théorème de Thalès
Trouver la longueur x.
Exercice 12 – Inéquation du second degré
Résoudre l’inéquation suivante :

Exercice 13 – Comparer les fonctions
Comparer les fonctions  et
et 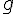 définies par :
définies par :
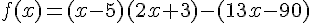
et
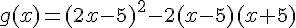
Exercice 14 – Développer et factoriser un polynôme
Soit le polynôme 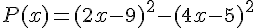 .
.
1. Développer P(x) .
2. Factoriser P(x) .
3. Donner le tableau de signes de P(x).
4. Résoudre l’inéquation 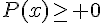 .
.
Exercice 15 – Résoudre des équations
Résoudre les équations suivantes dans  .
.
1. 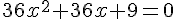 .
.
2. 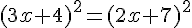 .
.
Exercice 16 – Etude de polynômes
Pour chacun des polynômes P(x) suivants, réaliser le travail suivant :
1. Développer P(x).
2. Factoriser P(x).
3. Résoudre P(x) = 0.
4. Donner le tableau de signes de P(x).
5. Vérifier les résultats obtenus à l’aide de la calculatrice (courbes).
– 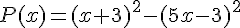 .
.
– 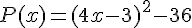 .
.
Exercice 17 – Nombre de solutions d’une équation
Quel est le nombre de solutions dans  de l’équation suivante :
de l’équation suivante :
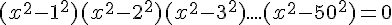
Justifier votre réponse .
Exercice 18 – Résoudre les équations
Résoudre les équations suivantes sur  :
:
1. 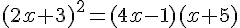 .
.
2. 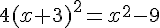
3. 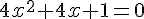
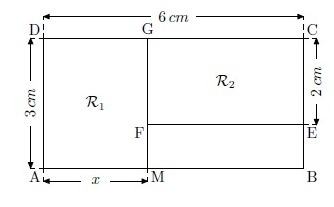
Exercice 19 – Géométrie, équations et inéquations
Description de la figure ci-dessus :
– ABCD est un rectangle tel que AD = BC = 3cm;
– M est un point du segment [AB] tel que AM = x avec 0 < x < 6 et x exprimé en cm;
– E est le point du segment [CB] tel que CE = 2cm.
On note R1 le rectangle AMGD et R2 le rectangle FECG.
1) P1 et P2 sont les périmètres des rectangles R1 et R2, exprimés en cm.
a) Exprimer P1 et P2 en fonction de x.
b) Pour quelle valeur de x les périmètres P1 et P2 sont-ils égaux ?
2) S1 et S2 sont les aires des rectangles R1 et R2 exprimées en cm².
a) Exprimer S1 et S2 en fonction de x.
b) Pour quelles valeurs de x a-t-on : S2 < S1 ?
Affirmations vraies ou fausses
Les affirmations suivantes sont-elles vraies ou fausses ?
1. 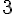 et
et  sont solutions de l’équation
sont solutions de l’équation  .
.
2. L’équation 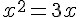 équivaut à l’équation
équivaut à l’équation 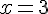 .
.
3. Pour tout  ,
, 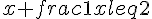 .
.
Toute réponse devra être justifiée .
Exercice 21 – Résoudre les équations suivantes :
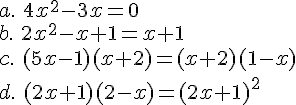
Exercice 22 – Résoudre l’inéquation suivante :

Exercice 23 – Résoudre une inéquation
Résoudre l’inéquation 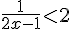 .
.
Exercice 24 – Trouver des nombres
1. Trouver deux entiers consécutifs dont le produit augmenté de 7 est égal au carré de l’entier suivant.
2. Trouver les nombres dont le carré est égal au triple.
3. Trouver les nombres dont le triple du carré est égal au double du nombre.
Exercice 25 – Factorisation et équation
1. Factoriser le polynôme 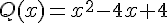 .
.
2. Résoudre l’équation 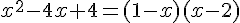 .
.
Exercice 26 – Tableau de signes d’un polynôme
Soit le polynôme 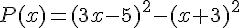 .
.
1. Montrer que 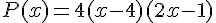 .
.
2. Donner le tableau de signes de 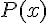 .
.
3. Résoudre l’inéquation  .
.
Exercice 27 – Résoudre deux équations
Résoudre les équations suivantes :
1. 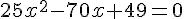 .
.
2.  .
.
Exercice 28 – Représentation graphique et inéquations
1. Représenter dans un même repère orthonormal :
– la fonction  définie sur
définie sur  par
par 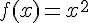 .
.
– la fonction 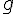 définie sur
définie sur  par
par 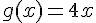 .
.
2. Utiliser ces représentations graphiques pour résoudre graphiquement :
a. l’équation  .
.
b. l’inéquation 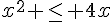 .
.
3. Retrouver les résultats précédents par le calcul.
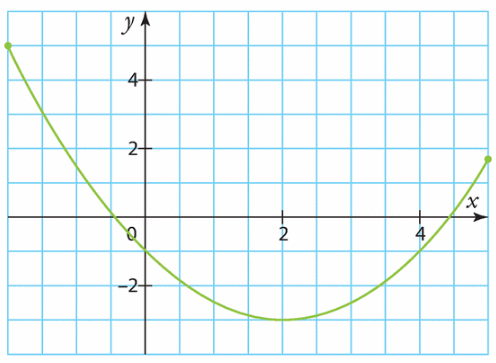
Exercice 29 – Second degré et clôture d’une chèvre
Benoit en a assez de tondre l’herbe devant chez lui.
Il décide donc d’acheter une chèvre qui s’occupera de cette tache. Pour ne pas que cette dernière parte dévorer les salades du voisin, il souhaite délimiter une zone rectangulaire accolé à sa maison dans laquelle son quadrupède pourra évoluer. Il achète pour cela une clôture de 100 mètres de long. Benoit se demande quelles dimensions il doit donner à sa clôture pour que sa surface délimitée soit la plus grande possible.
On désigne par x les longueurs en mètres des deux cotés perpendiculaire à sa maison.
1) Exprimer en fonction de x la longueur du troisième coté de la clôture.
2) a) Exprimer en fonction de x, l’aire f(x) de la zone délimitée par la clôture et la maison.
b) Résoudre l’inéquation 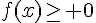 .
.
En déduire les seules valeurs de x susceptibles de nous intéresser.
3) a) Vérifier que pour tout x appartient à [0;50], 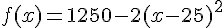 .
.
b) Dresser le tableau de variations de f sur [0;50] ( Justifier).
c) Donner alors les dimensions de la zone rectangulaire.
4) a) Résoudre graphiquement puis par le calcul l’équation f(x)=450.
b) Donner une interprétation du résultat de la question précédente.
Exercice 30 – Tableau de signe
En utilisant le tableau de signe, résoudre :

Exercice 31 – Equation du second degré
résoudre l’inéquation suivante :
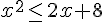
Exercice 32 – Rectangle d’or
Un rectangle est appelé rectangle d’or lorsque :
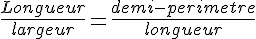 .
.
On considère un rectangle d’or de côtés 1 et x, avec 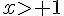 .
.
1. Montrer que x vérifie l’équation : 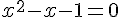 .
.
2. Dresser le tableau de valeur, puis la courbe représentative de cette fonction.
3. Résoudre graphiquement l’équation de la question 1 (au dixième près ) .
4. Vérifier que le réel 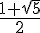 est solution de cette équation et en déduire les dimensions du rectangle d’or.
est solution de cette équation et en déduire les dimensions du rectangle d’or.
Remarque : Le nombre 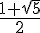 est appelé nombre d’or.
est appelé nombre d’or.
Exercice 33 – Tableau de signes
Voici l’énoncé: utiliser un tableau de signe pour étudier le signe de cette expression, x étant un nombre réel:
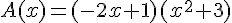 .
.
Exercice 34 – Etude du signe d’une fonction du second degré
f est la fonction définie sur R par f(x)=(3x+2)(4-x).
C est la courbe représentative de f dans un repère.
a)Calculer les abscisses des points d’intersection de la courbe C avec l’axe des abscisses.
b)Représenter graphiquement la fonction f à l’écran d’une calculatrice.
Conjecturer le signe de f(x) selon les valeurs de x.
c)Rappeler le signe de ax+b suivant les valeurs de x (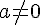 ).
).
Exercice 35 – Factorisation et équations
Soit 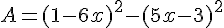 .
.
1) Développer et réduire A .
2) Calculer A pour 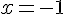 puis pour
puis pour 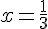 .
.
3) Factoriser A.
4) Résoudre l’équation A=0.
Exercice 36 – Triangle rectangle, équation et inéquation
ABC est un triangle rectangle en A tel que AB=9cm et AC=12cm.
Où placer le point M sur l’hypoténuse du triangle de façon que la somme des distances de M aux deux autres côtés du triangle soit égale à 10cm?
Exercice 37 – Résoudre les équations :
1. 7x2 – 5x = 0
2. 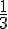 x2 = 5x
x2 = 5x
3. (-3x+1)(x-4) = 2x(x-4)
4. (2x+3)(x+5) = 15
5. (-3x+2)(x+1) = 2
Exercice 38 – Equation du troisième degré
Résoudre l’équation suivante :
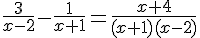
Exercice 39 – Résoudre les équations suivantes :
1. 7x2 – 5x = 0
2. 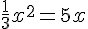
3. (-3x+1)(x-4) = 2x(x-4)
4. (2x+3)(x+5) = 15
5. (-3x+2)(x+1) = 2
Exercice 40 – Factorisation et équations
Résoudre les équations après avoir effectué une factorisation :
1. x2 – 3x = 0
2. -2x2 + 8x = 0
3. 3x2 = 18x
4. (2x-1)(x+1) – (2x-1)(3x-5) = 0.
Exercice 41 – Résoudre l’inéquation suivante :
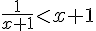
Exercice 42 – Résoudre les équations suivantes :
1.  .
.
2. 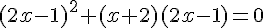 .
.
3. 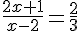 .
.
4.  .
.
Exercice 43 – Développer et factoriser
On donne : A(x) = 3 (x + 3)(x – 4) + 2 (3 x – 4)(x – 4)
et B(x) = (2 x – 3)² – (x + 1)²
1° a) Développer et factoriser A(x).
b) Développer et factoriser B(x).
2° En choisissant l’écriture la plus adaptée, résoudre les équations suivantes :
a) A(x) = – 4
b) B(x) = 0
c) B(x) = A(x)
Exercice 44 :
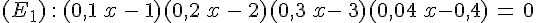
(E2) : 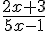 = 2
= 2
(E3) : 4 x − 0,8 = 2 − 1,6 x
(E4) : 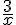 =
=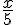
(E5) : (x − 2)2 =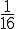 (5 − 2 x)2
(5 − 2 x)2
(E6) : 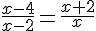
(E7) : (x + 1)(3 − 2 x) = 4 x2 − 9
(E8) : 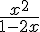 = −1
= −1
(E9) : (x + 2)2 = 2(x2 − 4)
(E10) : 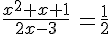
Exercice 45 :
Résoudre dans  les équations suivantes :
les équations suivantes :
a) 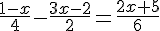
b) 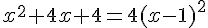
(On montrera que cette équation est équivalente à : 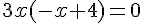 )
)
c) 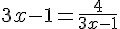
(On montrera que cette équation est équivalente à : 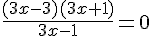 .
.
Exercice 46 :
Factoriser en utilisant une identité remarquable.
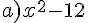
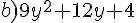

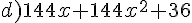
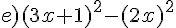
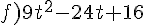
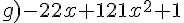
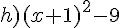
Exercice 47 :
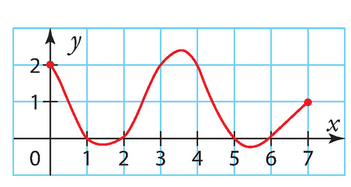
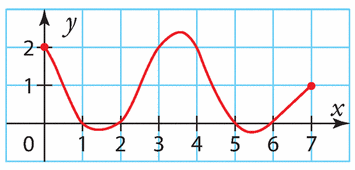
Voici la courbe représentative d’une fonction f définie sur [0;7].
Estimer les solutions des équations suivantes.
a) f(x)= 2 b) f(x) = 0 c) f(x) = – 1 d) f(x) = 1.
Exercice 48 :
Pour chacune des fonctions dont on donne les expressions ci-dessous,
essayer d’établir le plus grand ensemble de définition possible.
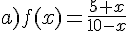
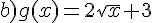
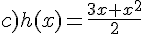
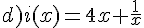
Exercice 49 :
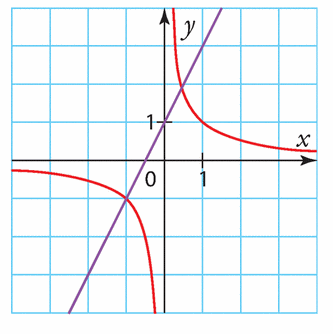
On considère les courbes représentatives de la fonction inverse, notée f, et
de la fonction affine g définie x sur R par g(x) = 2x + 1.
Elles sont tracées dans le repère ci-dessous.
1. Repérer les courbes associées aux deux fonctions.
2. Résoudre graphiquement l’équation  .
.
3. a) Développer l’expression (2x – 1)(x+ 1).
b) Retrouver algébriquement les résultats obtenus à la question 2.
Exercice 50 :
Les équivalences suivantes sont-elles vraies ou fausses ? (On justifiera, et si l’équivalence est fausse, on ajoutera à l’équation de droite ce qu’il faut pour qu’elle devienne équivalente à l’équation de gauche)
1) 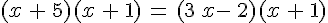
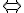
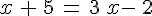
2) 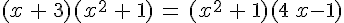
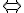
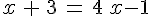
3) 
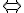
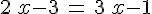
Exercice 51 :
Résoudre dans  les équations suivantes.
les équations suivantes.
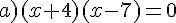
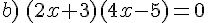
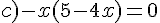
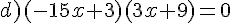

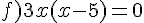
Exercice 52 :
Résoudre dans  les équations suivantes.
les équations suivantes.
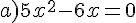
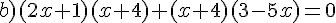
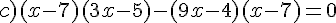
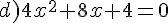
Exercice 53 :
Résoudre dans  les équations suivantes.
les équations suivantes.

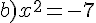
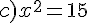
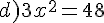
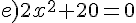
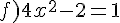
Exercice 54 :
Résoudre dans  les équations suivantes.
les équations suivantes.
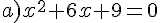

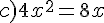
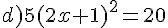

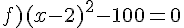
Exercice 55 :
Résoudre dans  les équations suivantes.
les équations suivantes.
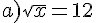
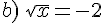
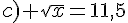
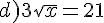
Exercice 56 :
Résoudre dans  les équations suivantes.
les équations suivantes.
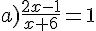
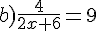

Exercice 57 :
On étudie dans un certain milieu l’évolution d’une population de bactéries.
Le nombre de bactéries en milliers a été modélisé en fonction du temps
écoulé en jours sur les dix premiers jours d’étude par la fonction N définie
par 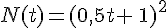 pour tout nombre réel
pour tout nombre réel ![t \in [0;10]](https://mathovore.fr/latex-images/0f67e219cd70b81cfb51d4646830ebc0.png) .
.
Donner une estimation du nombre de bactéries au bout d’un jour.
Au bout de combien de temps le nombre de bactéries a-t-il atteint 16 000 ?
Exercice 58 :
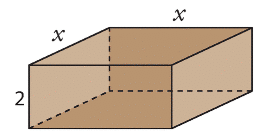
On veut construire une boîte en bois avec couvercle ayant une base carrée de côté  et
et
une hauteur égale à 2.
1. Montrer que la surface extérieure de la boîte est donnée
en fonction de  par la formule
par la formule  .
.
2. Pour quelle(s) valeur(s) de  la boîte a t-elle une surface extérieure égale à 72?
la boîte a t-elle une surface extérieure égale à 72?
Exercice 59 :
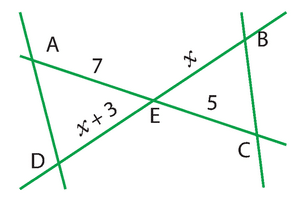
Pour quelle(s) valeur(s) de x les droites (AB) et (CD) sont-elles parallèles ?
Exercice 60 :
Soient x et y deux réel tels que 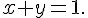
On pose 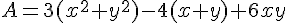
1) Calculer A pour  puis
puis 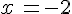 .
.
2) Développer  .
.
En déduire une simplification de A puis montrer que si 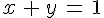 alors
alors 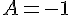 .
.
Exercice 61 :
Résoudre dans R :
1) 2 x – 5 < 3 x – 7
2) 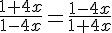
3) x2 + x + 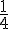 < (2 x + 1)2
< (2 x + 1)2
Exercice 62 :
1) Démontrer que pour tout réel x, on a 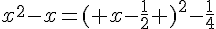 .
.
2) Soient deux réels x et y tels que x + y = 1, démontrer que :
a) x y < 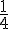 b) x2 + y2 >
b) x2 + y2 >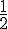
Exercice 63:
Déterminer le signe des expressions suivantes :
|
a) x2 + 1 |
b) – |
c) (x – 1)² + 4 |
d) –x2 – 7 |
|
e) –(–x – 2)² |
f) 1 + |
g) |
Exercice 64 :
Dresser, dans chacun des cas suivants, le tableau de signes de A(x).
a) A(x) s’annule en 5 et –2 ; A(x) est strictement positif pour x supérieur à 5 ou inférieur à –2 et A(x) < 0 sur ]–2 ; 5[.
b) A(x) ≤ 0 pour x 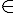 [–3 ; 4] et A(x) ≥ 0 pour x
[–3 ; 4] et A(x) ≥ 0 pour x 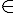 ]–
]– ; –3] [4 ; +
; –3] [4 ; +  [.
[.
c) A(x) n’existe pas en –1 ; le réel 3 est l’unique solution de l’équation A(x) = 0 et A(x) ≥ 0 sur ]–  ; –1[ ]–1 ; 3] et A(x) est négatif pour x ≥ 3.
; –1[ ]–1 ; 3] et A(x) est négatif pour x ≥ 3.
Exercice 65 :
Étudier le signe des expressions suivantes dans un tableau de signes.
a) (5x – 1)(1 – x) b) (3x + 4)(2x + 3) c) 3x(x – 2)
d) (2x + 1)(–5 – x)(x – 7) e) 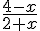 f)
f) 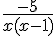
Exercice 66:
Étudier le signe des expressions suivantes après avoir factorisé ou mis au même dénominateur.
a) (2x – 1)(2 + x) – (2x – 1)² b) x2 – (2x + 1)² c) 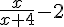
Exercice 67 :
1/ Déterminer une expression f(x) dont le tableau de signes est :
|
x |
– |
–2 |
3 |
+ |
|||
|
signe de f(x) |
+ |
0 |
– |
0 |
+ |
2/ Déterminer une expression g(x) dont le tableau de signes est :
|
x |
– |
1 |
4 |
+ |
|||
|
signe de g(x) |
– |
║ |
+ |
0 |
– |
Exercice 68:
L’étude du signe de l’expression B(x) a permis d’établir le tableau ci-dessous :
|
x |
– |
–2 |
1 |
3 |
+ |
||||
|
signe de B(x) |
– |
0 |
+ |
║ |
+ |
0 |
– |
Les affirmations suivantes sont-elles vraies ?
a) B(4,5) est négatif. b) B(1) = 0
c) –2 et 3 sont les solutions de l’équation B(x) = 0.
d) B(0) > 0 e) Si x < 0 alors B(x) < 0.
f) L’ensemble des solutions de B(x) ≤ 0 est ]–  ; –2] [3 ; +
; –2] [3 ; + [.
[.
g) Les nombres tels que B(x) > 0 sont les nombres vérifiant –2 ≤ x ≤ 3.
Exercice 69 :
Résoudre les inéquations suivantes :
a) (2x – 5)(–x – 3) ≥ 0 b) (x – 4)(2x + 3) + (x – 4)(x – 7) ≤ 0
c) (2x – 5)(–x – 3) ≤ –15 d) (x + 1)² > (2x – 3)²
e)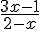 ≤ 0 f)
≤ 0 f) 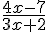 < 4
< 4
g) (–x + 1)(6x – 5)(x + 3) + (–x + 1)(6x – 5)(x – 5) > 0
Exercice 70 :
Soit f et g les fonctions définies sur par f(x) = x2 et g(x) = 4x – 3
1/ a) Tracer les courbes représentant ces deux fonctions sur l’écran de la calculatrice.
b) En déduire l’ensemble des solutions de l’inéquation f(x) ≥ g(x).
2/ a) Développer (x – 1)(x – 3).
b) Résoudre, par le calcul cette fois, f(x) ≥ g(x).
Exercice 71 :
Voici la courbe représentative d’une fonction f définie sur [0;7].
Estimer les solutions des équations suivantes.
a) f(x)=2 b) f(x) = 0 c) f(x) =- 1 d) f(x) = 1
Exercice 72:
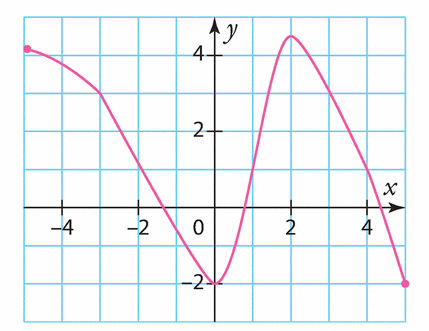
Voici la courbe représentative d’une fonction g définie sur [—5 ; 5].
Estimer les solutions des équations.
a) g(x) = 2
b) g(x) = —3
c) g(x) = 4
d) g(x) =- 1
Exercice 73 :
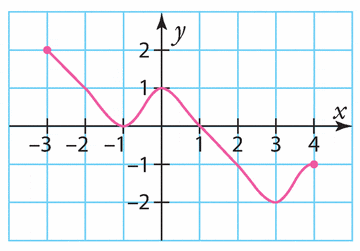
Voici la courbe représentative d’une fonction k définie sur [ – 3 ; 4].
Estimer les solutions des équations et inéquations suivantes.
a) k(x) = 1
b) k(x) = 0
c) k(x) > – 1
d) k(x) < 0
e) 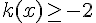
f) 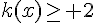
Exercice 74:
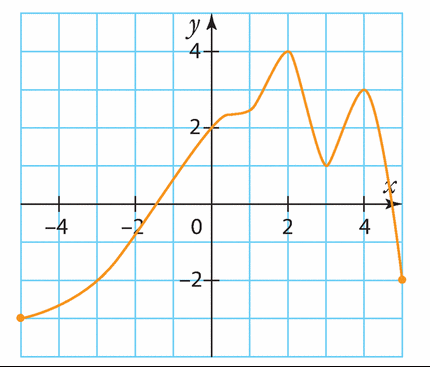
Voici la courbe représentative d’une fonction h définie sur [—5 ; 5].
Estimer les solutions des inéquations suivantes.
a) 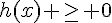
b) h(x) < —4
c) h(x) < —2
d) h(x) > 2
Exercice 75:
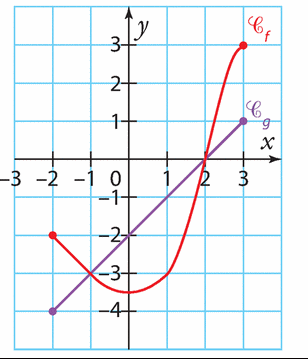
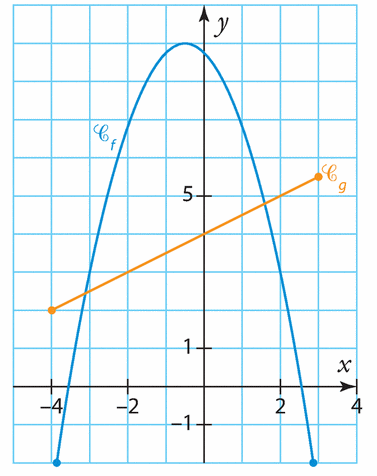
Voici les courbes représentatives d’une fonction f et d’une fonction g définies sur [ – 2 ; 3].
Résoudre graphiquement les équations et inéquations.
a) g(x) = f(x)
b) 
c) f(x) < —3
d) g(x) < 2
e)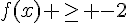
Exercice 76 :
Voici les courbes représentatives de deux fonctions f et g définies sur [—4 ; 3].
Résoudre graphiquement les équations et inéquations suivantes.
a) f(x) = 8
b) f(x) < 0
c) f(x) = g(x)
d) 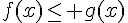
Exercice 77 :
Pour chacune des courbes ci-dessous, dire si elle semble être la courbe représentative d’une fonction paire, d’une fonction impaire ou d’une fonction qui n’est ni paire ni impaire.
Exercice 78 :
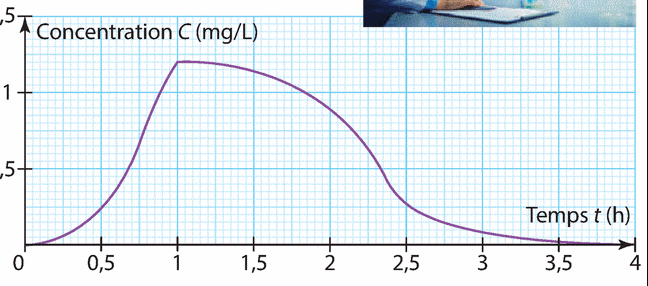
On a mesuré en continu pendant quatre heures, la concentration C d’un médicament dans le sang d’un
patient. La fonction C est représentée ci-dessous.
1. Quelle est Ia concentration du médicament dans le sang au bout de 2h ?
a) environ 0,5 b) environ 1
c) environ 1.5 d) environ 0,9
2. Laquelle (lesquelles) de(s) (in)équations suivantes a pour solution l’intervalle de temps où la concentration du
médicament est au plus égale à 1 ?
a) C(t)>1 b) C(t)=1
c) C(t)<1 d) C(t)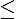 1
1
3. Au bout de combien de temps la concentration dans le sang est-elle égale à 0.5 mg/L ?
a) 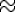 40 min b)
40 min b) 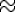 2 h 20 min c)
2 h 20 min c) 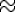 0,667 h
0,667 h
4. Ce médicament est jugé efficace quand la concentration dans le sang dépasse 0.75 mg/L.
Quelle est donc sa période d’efficacité ? (Arrondir grossièrement.)
a) jusqu’à 2 h b) jusqu’à 4h
c) dès 45 min d) entre 0,75 h et 2,2 h
5. Au de combien de temps le médicament est-il le plus concentré ?
a)  1h b)
1h b)  1 h 30 min c)
1 h 30 min c)  1 h 50 min d)
1 h 50 min d)  6h
6h
6. Quelle est alors Ia concentration du médicament dans le sang en mg/L ?
a)  1 b)
1 b)  1,2 c)
1,2 c)  1,25 d)
1,25 d)  5.8
5.8
Exercice 79 :
Une fonction f a les propriétés suivantes :
— elle est définie sur [0 ; 8] ;
— l’équation f(x) = 3 a deux solutions : 1 et 3 ;
— l’image de 0 est 1 ;
— l’inéquation  a pour ensemble de solution [5 ; 7].
a pour ensemble de solution [5 ; 7].
Tracer dans un repère une courbe possible pour la fonction f.
Exercice 80 :
- Trouver les coordonnées du ou des points d’intersection des courbes d’équations
 et
et 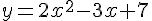 .
. - Même question pour les courbes d’équations
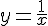 et
et 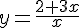 .
.
Exercice 81:
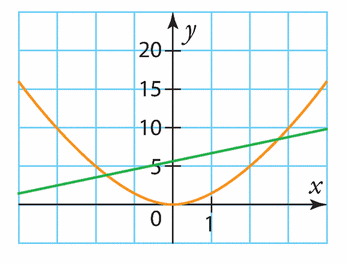
On considère les courbes représentatives de la fonction carré, notée f, et de la fonction affine g définie sur  par
par 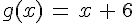 .
.
Elles sont tracées dans le repère ci-dessous.
1. Repérer les courbes associées aux deux fonctions.
2. Résoudre graphiquement l’équation 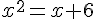 .
.
3. a) Développer l’expression 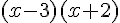 .
.
b) Retrouver algébriquement les résultats obtenus la question 2.
Exercice 82 :
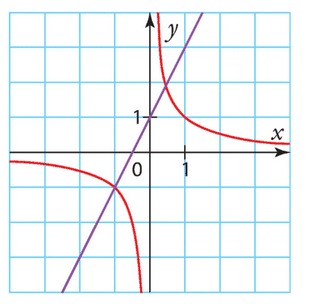
On considère les courbes représentatives de la fonction inverse, notée f, et
de la fonction affine g définie sur  par g(x) = 2x+ 1.
par g(x) = 2x+ 1.
Elles sont tracées dans le repère ci-dessous.
1. Repérer les courbes associées aux deux fonctions.
2. Résoudre graphiquement l’équation  .
.
3.a) Développer l’expression 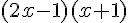 .
.
b) Retrouver algébriquement les résultats obtenus à la question 2.
Exercice 83:
On donne ci-dessous la courbe représentative de la fonction f définie sur [—2 ; 5] par 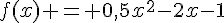 .
.
1. Estimer graphiquement les deux solutions de l’équation f(x) = 1.
2. Voici un tableau de valeurs de la fonction f.
a) Donner un encadrement d’une des solutions de l’équation f(x) = 1.
b) Quelle est la précision de cette approximation ?
3. A l’aide de la calculatrice, donner un encadrement au dixième près, puis au centième près de l’autre solution.
Télécharger et imprimer ce document en PDF gratuitement :
Vous avez la possibilité de télécharger puis d'imprimer gratuitement ce document «Équations et inéquations : exercices de maths en 2de corrigés en PDF.» au format PDF.
Ressources de seconde
Cours de seconde
D'autres cours et exercices à consulter
🤖 Exercices IA Interactifs ✨

Des milliers d'exercices interactifs conformes aux programmes officiels. Apprenez, pratiquez et progressez à votre rythme.
Exercices interactifsL'équipe Mathovore
12 Enseignants Titulaires
Collectif d'enseignants titulaires de l'Éducation Nationale, spécialisés en mathématiques en primaire, au collège, au lycée et post-bac.
Notre équipe collaborative enrichit constamment nos ressources pédagogiques.
Nos applications
Téléchargez gratuitement la dernière version de nos applications.